
儿何鞋 68◆Yn 色w 图7.9偏心受压构件的截面应变分布 7.1.3偏心受压构件的M-N相关曲线 偏心受压构件是弯矩和轴力共同作用的构件,轴力与弯矩对于构件的作用效应存在着叠 加和制约的关系,亦即当给定轴力N时,有其唯一对应的弯矩M,或者说构件可以在不同 的N和M的组合下达到其极限承载能力。 对于偏心受压短柱,由其截面承载力的计算分析可以得到图7-10所示的偏心受压构件 MN相关曲线图。在图70中,动段表示大偏心受压时的MN相关曲线,为二次抛物线。 随着轴向压力N的增大,截面能承担的弯矩也相应提高。 b点为钢筋与受压混凝土同时达到其强度极限值的界限状态。此时,偏心受压构件承受 的弯矩M最大。 图7-10偏心受压构件的N曲线图 cb段表示小偏心受压时的MN相关曲线,是一条接近于直线的二次函数曲线。由曲线 走向可以看出,在小偏心受压情况下,随者轴向压力的增大,截面所能承担的弯矩反而降低。 在图7-10中,c点表示轴心受压的情况,a点表示受弯构件的情况。图中曲线上的任 点d的坐标就代表截面强度的一种M和V的组合。若任意点d位于曲线ac的内侧,说明 截面在该点坐标给出的M和N的组合未达到承载能力极限状态:若d点位于图中曲线b 的外侧则表明截面的承载力不足
7-6 几何轴线 图 7-9 偏心受压构件的截面应变分布 7.1.3 偏心受压构件的 M-N 相关曲线 偏心受压构件是弯矩和轴力共同作用的构件,轴力与弯矩对于构件的作用效应存在着叠 加和制约的关系,亦即当给定轴力 N 时,有其唯一对应的弯矩 M,或者说构件可以在不同 的 N 和 M 的组合下达到其极限承载能力。 对于偏心受压短柱,由其截面承载力的计算分析可以得到图 7-10 所示的偏心受压构件 M-N 相关曲线图。在图 7-10 中,ab 段表示大偏心受压时的 M-N 相关曲线,为二次抛物线。 随着轴向压力 N 的增大,截面能承担的弯矩也相应提高。 b 点为钢筋与受压混凝土同时达到其强度极限值的界限状态。此时,偏心受压构件承受 的弯矩 M 最大。 ( ) 受 压 破 坏 受 拉 破 坏 图 7-10 偏心受压构件的 M-N 曲线图 cb 段表示小偏心受压时的 M-N 相关曲线,是一条接近于直线的二次函数曲线。由曲线 走向可以看出,在小偏心受压情况下,随着轴向压力的增大,截面所能承担的弯矩反而降低。 在图 7-10 中,c 点表示轴心受压的情况,a 点表示受弯构件的情况。图中曲线上的任一 点 d 的坐标就代表截面强度的一种 M 和 N 的组合。若任意点 d 位于曲线 abc 的内侧,说明 截面在该点坐标给出的 M 和 N 的组合未达到承载能力极限状态;若 d 点位于图中曲线 abc 的外侧则表明截面的承载力不足

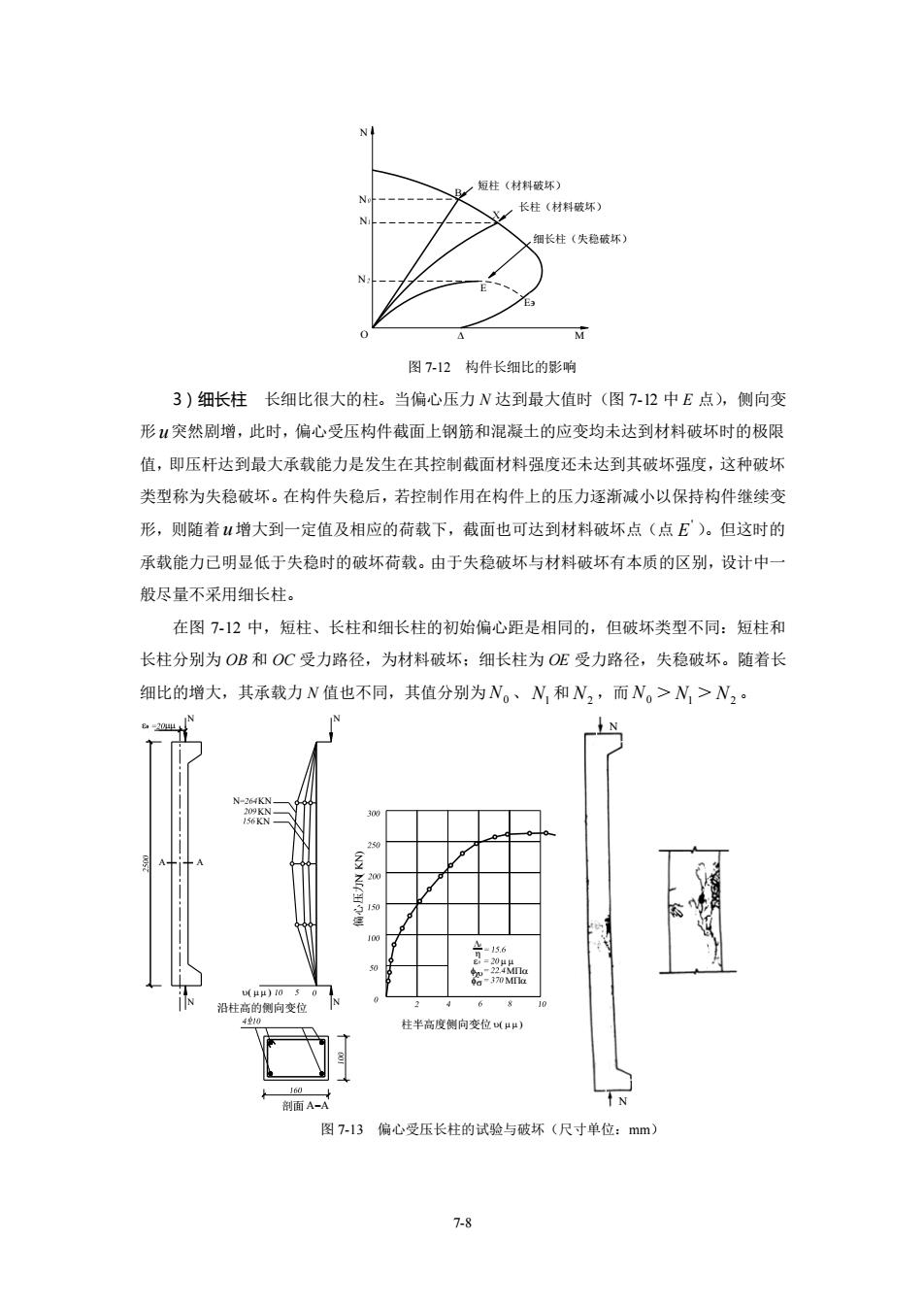
72偏心受压构件的纵向弯曲 钢筋混凝土受压构件在承受偏心力作用后,将产生纵向弯曲变形,即会产生侧向变形(变 位)。对于长细比小的短柱,侧向挠度小,计算时一般可忽略其影响。而对长细比较大的长 柱,由于侧向变形的影响,各截面所受的弯矩不再是We,而变成N(。+y)(图7I1),y 为构件任意点的水平侧向变形。在柱高度中点处,侧向变形最大,截面上的弯矩为N(,+W)。 ▣随着荷载的增大而不断加大,因而弯矩的增长也越来越快。一般把偏心受压构件截面弯矩 中的N,称为初始弯矩或一阶弯矩(不考虑构件侧向变形时的弯矩),将Mu或My称为附 加弯矩或二阶弯矩。由于二阶弯矩的影响,将造成偏心受压构件不同的破坏类型。 N() 图-1偏心受压构件的受力图式 7.2.1偏心受压构件的破坏类型 钢筋混凝士偏心受压构件按长细比可分为短柱、长柱和细长柱。 1)短柱偏心受压短柱中,虽然偏心力作用将产生一定的侧向变形,但其值很小 一般可忽略不计。即可以不考虑二阶弯矩,各截面中的弯矩均可认为等于N。,弯矩M与 轴向力N呈线性关系。 随着荷载的增大,当短柱达到极限承载能力时,柱的截面由于材料达到其极限强度而破 坏。在MN相关图中,从加载到破坏的路径为直线,当直线与截面承载力线相交于B点时 就发生材料破坏,即图7-12中的OB直线。 2)长柱矩形截面柱,当8<h≤30时即为长柱。长柱受偏心力作用时的侧向变形u 较大,二阶弯矩影响已不可忽视,因此,实际偏心距是随荷载的增大而非线性增加,构件控 制截面最终仍然是由于截面中材料达到其强度极限而破坏,属材料破坏。图-3为偏心受 压长柱的试验结果。其截面尺寸、配筋与图7-6所示短柱相同,但其长细比为h=15.6,最 终破坏形态仍为小偏心受压,但偏心距已随N值的增加而变大。 偏心受压长柱在MN相关图上从加荷到破坏的受力路径为曲线,与截面承载力曲线相 交于C点而发生材料破坏,即图7-12中0C曲线。 7.7
7-7 7.2 偏心受压构件的纵向弯曲 钢筋混凝土受压构件在承受偏心力作用后,将产生纵向弯曲变形,即会产生侧向变形(变 位)。对于长细比小的短柱,侧向挠度小,计算时一般可忽略其影响。而对长细比较大的长 柱,由于侧向变形的影响,各截面所受的弯矩不再是 Ne0 ,而变成 0 N e y ( ) + (图 7-11),y 为构件任意点的水平侧向变形。在柱高度中点处,侧向变形最大,截面上的弯矩为 0 N e u ( ) + 。 u 随着荷载的增大而不断加大,因而弯矩的增长也越来越快。一般把偏心受压构件截面弯矩 中的 Ne0 称为初始弯矩或一阶弯矩(不考虑构件侧向变形时的弯矩),将 Nu 或 Ny 称为附 加弯矩或二阶弯矩。由于二阶弯矩的影响,将造成偏心受压构件不同的破坏类型。 =( +) 图 7-11 偏心受压构件的受力图式 7.2.1 偏心受压构件的破坏类型 钢筋混凝土偏心受压构件按长细比可分为短柱、长柱和细长柱。 1)短柱 偏心受压短柱中,虽然偏心力作用将产生一定的侧向变形,但其 u 值很小, 一般可忽略不计。即可以不考虑二阶弯矩,各截面中的弯矩均可认为等于 Ne0 ,弯矩 M 与 轴向力 N 呈线性关系。 随着荷载的增大,当短柱达到极限承载能力时,柱的截面由于材料达到其极限强度而破 坏。在 M-N 相关图中,从加载到破坏的路径为直线,当直线与截面承载力线相交于 B 点时 就发生材料破坏,即图 7-12 中的 OB 直线。 2)长柱 矩形截面柱,当 8<l0/h≤30 时即为长柱。长柱受偏心力作用时的侧向变形 u 较大,二阶弯矩影响已不可忽视,因此,实际偏心距是随荷载的增大而非线性增加,构件控 制截面最终仍然是由于截面中材料达到其强度极限而破坏,属材料破坏。图 7-13 为偏心受 压长柱的试验结果。其截面尺寸、配筋与图 7-6 所示短柱相同,但其长细比为 l0/h =15.6,最 终破坏形态仍为小偏心受压,但偏心距已随 N 值的增加而变大。 偏心受压长柱在 M-N 相关图上从加荷到破坏的受力路径为曲线,与截面承载力曲线相 交于 C 点而发生材料破坏,即图 7-12 中 OC 曲线
短柱《材料环 长柱〔材料被坏 长柱(失稳破 图7-12构件长细比的影响 3)细长柱长细比很大的柱。当偏心压力N达到最大值时(图7-12中E点),侧向变 形突然剧增,此时,偏心受压构件截面上钢筋和混凝士的应变均未达到材料破坏时的极限 值,即压杆达到最大承载能力是发生在其控制截面材料强度还未达到其破坏强度,这种破坏 类型称为失稳破坏。在构件失稳后,若控制作用在构件上的压力逐渐减小以保持构件继续变 形,则随着增大到一定值及相应的荷载下,截面也可达到材料破坏点(点E)。但这时的 承载能力已明显低于失稳时的破坏荷载。由于失稳破坏与材料破坏有本质的区别,设计中 般尽量不采用细长柱。 在图712中,短柱、长柱和细长柱的初始偏心距是相同的,但破坏类型不同:短柱利 长柱分别为OB和OC受力路径,为材料破坏:细长柱为OE受力路径,失稳破坏。随者长 细比的增大,其承载力N值也不同,其值分别为N。、N和N2,而N。>N>N N 柱半高度侧向变位】 N 图7-13偏心受压长柱的试验与破坏(尺寸单位:mm)
7-8 长柱(材料破坏) 细长柱(失稳破坏) 短柱(材料破坏) 图 7-12 构件长细比的影响 3)细长柱 长细比很大的柱。当偏心压力 N 达到最大值时(图 7-12 中 E 点),侧向变 形 u 突然剧增,此时,偏心受压构件截面上钢筋和混凝土的应变均未达到材料破坏时的极限 值,即压杆达到最大承载能力是发生在其控制截面材料强度还未达到其破坏强度,这种破坏 类型称为失稳破坏。在构件失稳后,若控制作用在构件上的压力逐渐减小以保持构件继续变 形,则随着 u 增大到一定值及相应的荷载下,截面也可达到材料破坏点(点 ' E )。但这时的 承载能力已明显低于失稳时的破坏荷载。由于失稳破坏与材料破坏有本质的区别,设计中一 般尽量不采用细长柱。 在图 7-12 中,短柱、长柱和细长柱的初始偏心距是相同的,但破坏类型不同:短柱和 长柱分别为 OB 和 OC 受力路径,为材料破坏;细长柱为 OE 受力路径,失稳破坏。随着长 细比的增大,其承载力 N 值也不同,其值分别为 N0 、 N1 和 N2 ,而 N0 > N1 > N2 。 偏心压力 ( ) 剖面 − 柱半高度侧向变位 ( ) 沿柱高的侧向变位 ( ) 图 7-13 偏心受压长柱的试验与破坏(尺寸单位:mm)

7.2.2偏心距增大系数 实际工程中最常遇到的是长柱,由于最终破坏是材料破坏,因此,在设计计算中需考虑 由于构件侧向变形(变位)而引起的二阶弯矩的影响。 偏心受压构件控制截面的实际弯矩应为 M=N(e+u)=N +u e 令 刀=6+”=1+“ (7-1) M=N.neo 刀称为偏心受压构件考虑纵向挠曲影响(二阶效应)的轴向力偏心距增大系数。 由式(7-1)可见,n越大表明二阶弯矩的影响越大,则藏面所承担的一阶弯矩N,在 总弯矩中所占比例就相对越小。应该指出的是,当,=0时,式(?)是无意义的。当偏心 受压构件为短柱时,则7=1。 《公路桥规》根据偏心压杆的极限曲率理论分析,规定偏心距增大系数计算表达式为 (7-2) 51=02+272≤10 (7-3a) 6=15-001≤10 (7-3b) 式中一一构件的计算长度,可参照表6-1或按工程经验确定 ,一—轴向力对截面重心轴的偏心距: 么一一截面的有效高度。对圆形截面取=r+,r及意义详见7.5节: h一截面的高度。对圆形截面取h=d,d,为圆形截面直径: 一一荷载偏心率对截面曲率的影响系数: 52—构件长细比对截面曲率的影响系数。 《公路桥规》规定,计算偏心受压构件正截面承载力时,对长细比L。>17.5(1为构 件裁面回转半径)的构件或长细比,h(矩形截面)>5、长细比,/d,(圆形截面)>4.4的构件 应考虑构件在弯矩作用平面内的变形(变位)对轴向力偏心距的影响。此时,应将轴向力对 截面重心轴的偏心距e,乘以偏心距增大系数)。 偏心受压构件的弯矩作用平面的意义见图-14的示意图。应该指出的,前述偏心受 压构件的破坏类型及破坏形态,均指在弯矩作用平面的受力情况。 7.9
7-9 7.2.2 偏心距增大系数 实际工程中最常遇到的是长柱,由于最终破坏是材料破坏,因此,在设计计算中需考虑 由于构件侧向变形(变位)而引起的二阶弯矩的影响。 偏心受压构件控制截面的实际弯矩应为 0 0 0 0 ( ) e u M N e u N e e + = + = 令 0 0 0 1 e u u e e + = = + (7-1) 则 0 M = N e 称为偏心受压构件考虑纵向挠曲影响(二阶效应)的轴向力偏心距增大系数。 由式(7-1)可见, 越大表明二阶弯矩的影响越大,则截面所承担的一阶弯矩 Ne0 在 总弯矩中所占比例就相对越小。应该指出的是,当 0 e =0 时,式(7-1)是无意义的。当偏心 受压构件为短柱时,则 = 1。 《公路桥规》根据偏心压杆的极限曲率理论分析,规定偏心距增大系数 计算表达式为 0 2 1 2 0 0 1 1 ( ) 1400( ) l e h h = + (7-2) 0 1 0 0.2 2.7 e h = + ≤1.0 (7-3a) h l 0 2 =1.15 − 0.01 ≤1.0 (7-3b) 式中 0 l ——构件的计算长度,可参照表 6-1 或按工程经验确定; 0 e ——轴向力对截面重心轴的偏心距; 0 h ——截面的有效高度。对圆形截面取 s h = r + r 0 , r 及 s r 意义详见 7.5 节; h ——截面的高度。对圆形截面取 h = d1, 1 d 为圆形截面直径; 1 ——荷载偏心率对截面曲率的影响系数; 2 ——构件长细比对截面曲率的影响系数。 《公路桥规》规定,计算偏心受压构件正截面承载力时,对长细比 o l i >17.5( i 为构 件截面回转半径)的构件或长细比 0 l h (矩形截面)>5、长细比 0 1 l d (圆形截面)>4.4 的构件, 应考虑构件在弯矩作用平面内的变形(变位)对轴向力偏心距的影响。此时,应将轴向力对 截面重心轴的偏心距 0 e 乘以偏心距增大系数 。 偏心受压构件的弯矩作用平面的意义见图 7-14 的示意图。应该指出的,前述偏心受 压构件的破坏类型及破坏形态,均指在弯矩作用平面的受力情况

矩作用平面 直于弯矩作用平面 图7-14矩形截面偏心受压构件的弯矩作用平面示意图 7.3矩形截面偏心受压构件 钢筋混凝士矩形截面偏心受压构件是工程中应用最广泛的构件,其截面长边为,短边 为b。在设计中,应该以长边方向的截面主轴面xx为弯矩作用平面(图7-14)。 矩形偏心受压构件的纵向钢筋一般集中布置在弯矩作用方向的截面两对边位置上,以 A,和A,来分别代表离偏心压力较远一侧和较近一侧的钢筋面积。当A,≠A,时,称为非对 称布筋:当A,=A,时,称为对称布筋。 7.3.1矩形截面偏心受压构件正截面承载力计算的基本公式 与受弯构件相似,偏心受压构件的正截面承载力计算采用下列基本假定: (1)截面应变分布符合平截面假定: (2)不考虑混凝土的抗拉强度: (3)受压混凝土的极限压应变6=0.0033~0.003,详见3.3.2节: (4)混凝土的压应力图形为矩形,应力集度为∫。,矩形应力图的高度x取等于按平 截面确定的受压区高度x乘以系数B,即x=。 矩形截面偏心受压构件正截面承载力计算图式如图7-15。 对于矩形截面偏心受压构件,用,表示纵向弯曲的影响,只要是材料破坏类型,无论 是大偏心受压破坏,还是小偏心受压破坏,受压区边缘混凝土都达到极限压应变,同一侧的 受压钢筋A,一般都能达到抗压强度设计值∫,而对面一侧的钢筋A,的应力,可能受拉 (达到或未达到抗拉强度设计值∫),也可能受压,故在图-15中以。,表示A,钢筋中的 应力,从而可以建立一种包括大、小偏心受压情况的统一正截面承载力计算图式。 7-10
7-10 弯矩作用平面 垂直于弯矩作用平面 图 7-14 矩形截面偏心受压构件的弯矩作用平面示意图 7.3 矩形截面偏心受压构件 钢筋混凝土矩形截面偏心受压构件是工程中应用最广泛的构件,其截面长边为 h,短边 为 b。在设计中,应该以长边方向的截面主轴面 x-x 为弯矩作用平面(图 7-14)。 矩形偏心受压构件的纵向钢筋一般集中布置在弯矩作用方向的截面两对边位置上,以 As 和 ' As 来分别代表离偏心压力较远一侧和较近一侧的钢筋面积。当 As ≠ ' As 时,称为非对 称布筋;当 As = ' As 时,称为对称布筋。 7.3.1 矩形截面偏心受压构件正截面承载力计算的基本公式 与受弯构件相似,偏心受压构件的正截面承载力计算采用下列基本假定: (1)截面应变分布符合平截面假定; (2)不考虑混凝土的抗拉强度; (3)受压混凝土的极限压应变 0.0033 ~ 0.003 cu = ,详见 3.3.2 节; (4)混凝土的压应力图形为矩形,应力集度为 cd f ,矩形应力图的高度 x 取等于按平 截面确定的受压区高度 c x 乘以系数 ,即 c x = x 。 矩形截面偏心受压构件正截面承载力计算图式如图 7-15。 对于矩形截面偏心受压构件,用 0 e 表示纵向弯曲的影响,只要是材料破坏类型,无论 是大偏心受压破坏,还是小偏心受压破坏,受压区边缘混凝土都达到极限压应变,同一侧的 受压钢筋 ' As ,一般都能达到抗压强度设计值 ' sd f ,而对面一侧的钢筋 As 的应力,可能受拉 (达到或未达到抗拉强度设计值 sd f ),也可能受压,故在图 7-15 中以 s 表示 As 钢筋中的 应力,从而可以建立一种包括大、小偏心受压情况的统一正截面承载力计算图式