由于,k,线性分组码是一个k维线性空间 因此,必可找到k个线性无关的矢量,能张成该线性空间 设C1,C2,.Ck是k个线性无关的矢量,则对任意 C,可有: C=m C+m2C2+...+mkCk C2 =(m1,m2,…mk Ck -mG G称为该分组码的生成矩阵
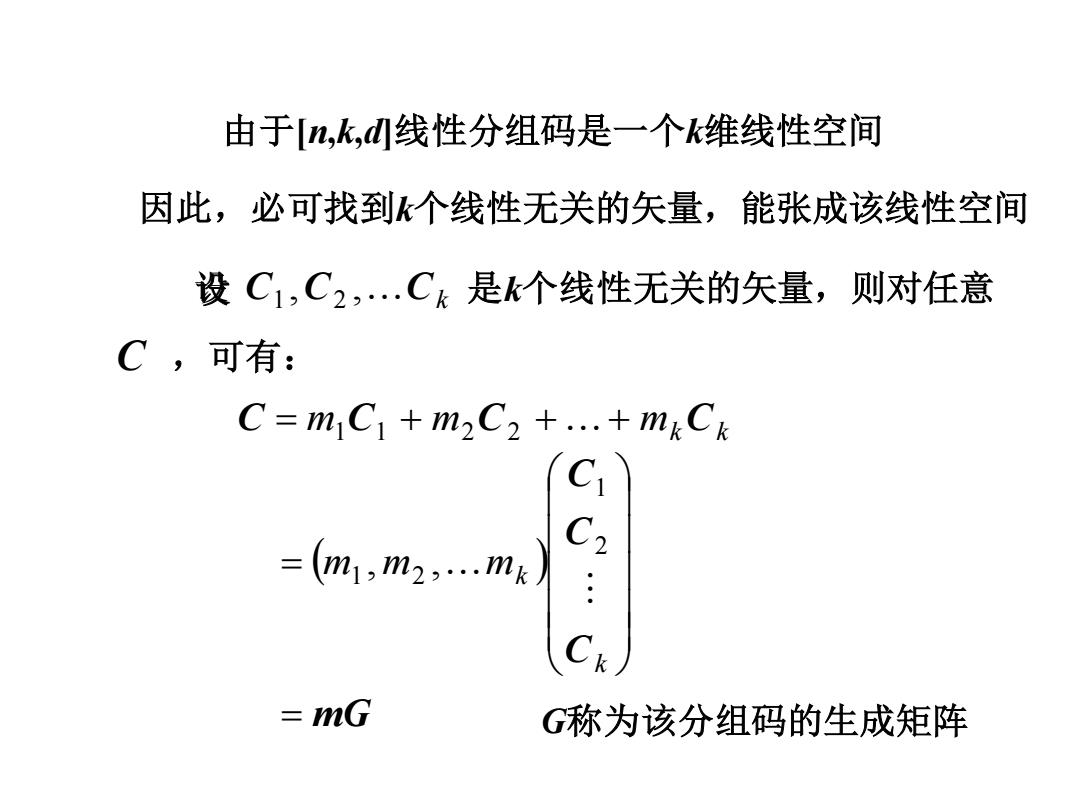
由于[n,k,d]线性分组码是一个k维线性空间 因此,必可找到k个线性无关的矢量,能张成该线性空间 设 C C Ck , , 1 2 是k个线性无关的矢量,则对任意 C ,可有: C = m1C1 + m2C2 ++ mkCk ( ) mG C C C = = k m m mk 2 1 1 2 , , G称为该分组码的生成矩阵 设

注: 1)生成矩阵G中的每一行都是一个码字 2) 任意k个线性独立的码字都可以作为生 成矩阵 3) 给定一个[n,k,d线性分组码,其生成矩 阵可有多个
注: 1) 生成矩阵G中的每一行都是一个码字 2) 任意k个线性独立的码字都可以作为生 成矩阵 3) 给定一个[n,k,d]线性分组码,其生成矩 阵可有多个

四、码的校验矩阵 一从线性方程组的角度描述分组码
四、码的校验矩阵 ——从线性方程组的角度描述分组码

Cn-1 Cn-2 …Cn-kCn-k-1Cn-k-2…C0 k个信息位 n-k个校验位 -k个校验位可用k个已知的信息位表示出来 Cn-k-1=hn-k-18-1*Cn-1+hn-k-18-2.Cm-2hn---kCn-k C--2=-2Cn-2-2Cm-22Cn-k Co=ho-1ChoCCn
n-k个校验位可用k个已知的信息位表示出来 个信息位 n k个校验位 n k n k k n n n k c c c c c c − −1 −2 − − −1 − −2 0 = + + + = + + + = + + + − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − n n n n n k n k n k n k n n n k n n n k n k n k n k n k n n n k n n n k n k n k c h c h c h c c h c h c h c c h c h c h c 0 0, 1 1 0, 2 2 0, 2 2, 1 1 2, 2 2 2, 1 1, 1 1 1, 2 2 1,
hn-k-1.n-1 hn-k-1.n-k 10 0. Cn- 0 hn-k-2.n-1 hn-k-2.n-k 01 0. Cn-2 0 。。 。。 ho.n-1 … hot,n-k 00.. Co 校验矩阵(n-k行,n列) 校验矩阵H与任意一个码字之积为零,因此有 H.G-0
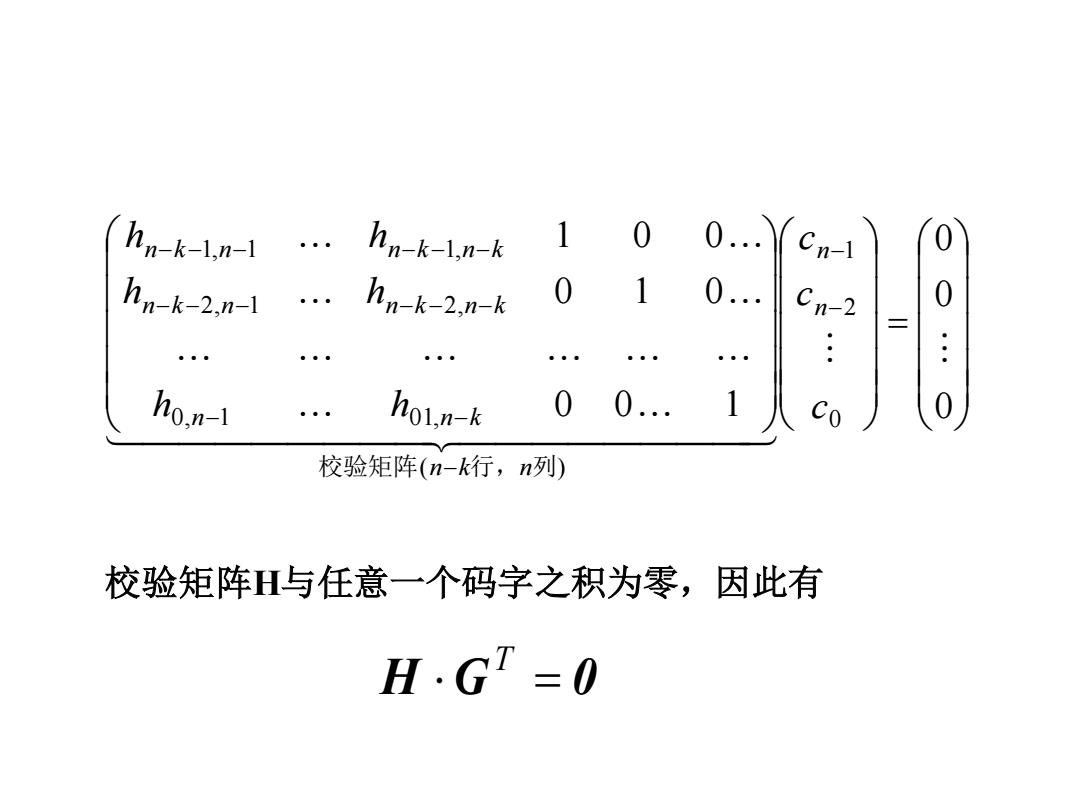
= − − − − − − − − − − − − − − − − − 0 0 0 0 0 1 0 1 0 1 0 0 0 2 1 ( ) 0, 1 01, 2, 1 2, 1, 1 1, c c c h h h h h h n n n k n n n k n k n n k n k n k n n k n k 校验矩阵 行, 列 校验矩阵H与任意一个码字之积为零,因此有 H G = 0 T