
若把这个方程组视为关于a,b,R的三元方程组,解得 a=3g,b=,R=是兴 将此结果代入Van der Waals方程并整理得 [皮+长-》=号罗 (1-21) 其中TT,p/中。和V./八分别为气体的温度、压力和体积与相应临界参数的比值,分别 称做对比温度T、对比压力p,和对比体积V。于是式(1-21)可写成 (+.--r (1-22) 式(1-22)称为Van der Waals对比方程,除对比参数之外,其中不再含有任何与物性有关 的常数,所以是反映Van der Waals气体普遍化规律的状态方程,故也称为普遍化Van der Wanls方程 对比方程是由Van der Waals方程经过纯数学处理后得来的,所以与Van der Waals 方程相比其普适性及计算的精度不会有任何提高。从这点来讲,式(1-22)没有任何实用价 值,与其用它来进行实际气体计算,还不如用Van der Waals方程本身。但是对比方程给 人们带来了新的启示。后来发现,其他一些实际气体状态方程也常常可以化成只含对比参 数的形式。这些对比方程告诉人们,实际气体的对比参数之间存在着一定的函数关系 fT,p.,,)=0 (1-23) 此式表明,各种不同的气体(后来发现,有些液体也是如此)只要处在相同的对比温度和对 比压力,就有相同的对比体积,称这些物质处在相同的对比状态。若某气体的对比参数等 于1,说明该气体处在临界点,所以对比参数与1偏离的大小可以代表气体现在所处的状 态与临界点的偏离程度。对比参数越远离1,则气体的状态越远离它的临界点。处在相同 对比状态的各种气体,说明它们与各自临界点的偏离程度相同。 进一步的实验表明,许多物质,当它们处于相同的对比状态时便具有相近的物性,如 热容,粘度,折射率,膨胀系数等,这个定律就叫做对比状态原理。对比状态原理只是一个 近似的规律,实验发现,组成、结构、分子大小越是相近的物质,就越能较好地服从对比状 态原理。尽管它是近似规律,但在工程上常利用这一规律,通过实验将许多物性表示成比 对状态的函数,这类公式虽然计算结果不是十分准确,但往往为工程设计带来极大的方 便 四、用压缩因子图计算实际气体 尽管目前已经发现许多实际气体的状态方程,但它们的普适性都不很高,于是人们便 想,能否像理想气体状态方程一样寻找一个适用子所有实际气体的状态方程呢?后来有人 建议,将理想气体状态方程进行校正便可以达到目的。即对于任意实际气体,可将其状态 方程写成 。=ZRT (1-24) 或 V =ZART (1-25) 17·

其中校正因子Z反映实际气体对理想气体的偏差。任何理想气体乙=1。实际气体的Z值 越远离1,说明它对理想气体的行为偏差越大。 由式(1-25)得 2==7 其中V为实际气体在温度T及压力p时的体积,而nRT/p则为如果气体是理想气体的 话,它在T,时所应具有的体积,用V1表示,于是上式可写成 (1-26) 式(1-26)告诉我们,气体的校正因子可以看作气体的体积与同温同压下理想气体的体积 之比。如果Z>1,表明气体的实际体积大子同温同压下理想气体的体积,表示与理想气体 相比,该气体难于压缩。相反,如果Z<1,则表明该气体具有比同温同压下的理想气体较 小的体积,即它比理想气体易于压缩。可见校正因子Z的数值,不仅表示气体对于理想气 体偏差程度的大小,而且还表示该气体难易压缩的程度,因此,通常称之为压缩因子, 由子压缩因子Z的数值反映实际气体对于理想行为的偏差程度,而实际气体的偏差 程度又与气体的状态有关,如温度越高,压力越低,气体就越接近理想气体,因此一种气体 的Z值随气体的状态不同而变化,即2并非气体的符性常数。由此可见,即使对于同一种 气体,其Z值也必须根据不同状态具体求取。 由式(1-24),任一气体在任意状态下的压缩因子为 将p,V。,T用相应的对比参数表示,则 z-2 即 z-0坐 (1-27) 其中(pV)/(RT)是气体处于临界点时的压缩因子,称临界压缩因子,用符号Z.表示,于 是式(1-27)可写成 (1-28) 此式适用子任意气体,任意-一种气体当p→0时都成为理想气体,即1im2=1。对式(1-28) 两端取极限 m2=2¥ (1-29) 即 乙,=1ym' (1-30) 对比状态原理f(T,pV,)=0可以写成 V.F(T.P) ·18

函数F对于所有气体(严格说是服从对比状态原理的气体)是同一个函数,两端同乘以 ./T,得 兴=是FT) 右端仍然是对比温度T,和对比压力P:的函数,令其为g(T,p,),则上式变为 =g(T) T. (1-31) 此式适用于任意气体,即对于所有气体,g是同一个函数,当p0时g的极限是一个与气 体种类无关的常数K,即 (1-32) 将式(1-32)代入(1-30)得 Z= (1-33) 这就告诉我们,各种不同的气体,它们的临界压缩因子都是相同的,都等予1/K。表1-4列 出了一些气体的2.值,这些气体都是遵守对比状态原理的气体。由表中看出,它们的Z。 值接近0.29。将式(1-33),(1-31)代入式(1-28),便得到任意气体的压缩因子 Z=家·gTp) 此式也可写成 Z =G(Tp.) (1-34) 此式说明,处在相同对比状态的各种气体,具有相同的压缩因于,也就是说,各种不同气体 如果处在与各自临界点相同偏离的状态,则它们对于理想气体的偏差程度是同的,为了 将式(1-34)的函数定量化,科学家们用30多种气体做了大量实验,根据实验结果计算出 各T,p,下的2的平均值,绘成图1-9。该图称为普遍化压缩因子图。图中的每一条曲线 都是一条等对比温度线,它代表在同一对比温度下Z随对比压力的变化关系。对于横坐 标上同一个对比压力所对应的不同曲线上的各点,则代表在同一对比压力下Z随对比温 度的变化关系。当,→0(即p→0》时,各对比温度度下的Z都趋近于1,即服从理想气体 状态方程。 表14一些气体的乙 气体Ne Ar CH.CF.N:O:CO 0.310.290.290.280.290.290.30 只要查得实际气体的临界参数,就可计算出在某一确定状态下它的对比参数,然后利 用普遍化压缩因子图,根据对比参数值从图上查出相应的Z值,再代入式(1-25),即可得 到实际气体的,V,T关系。工程上所用的压缩因于图有20多张,以分段图最为准确。从 而为实际气体的计算提供了方便。 。19
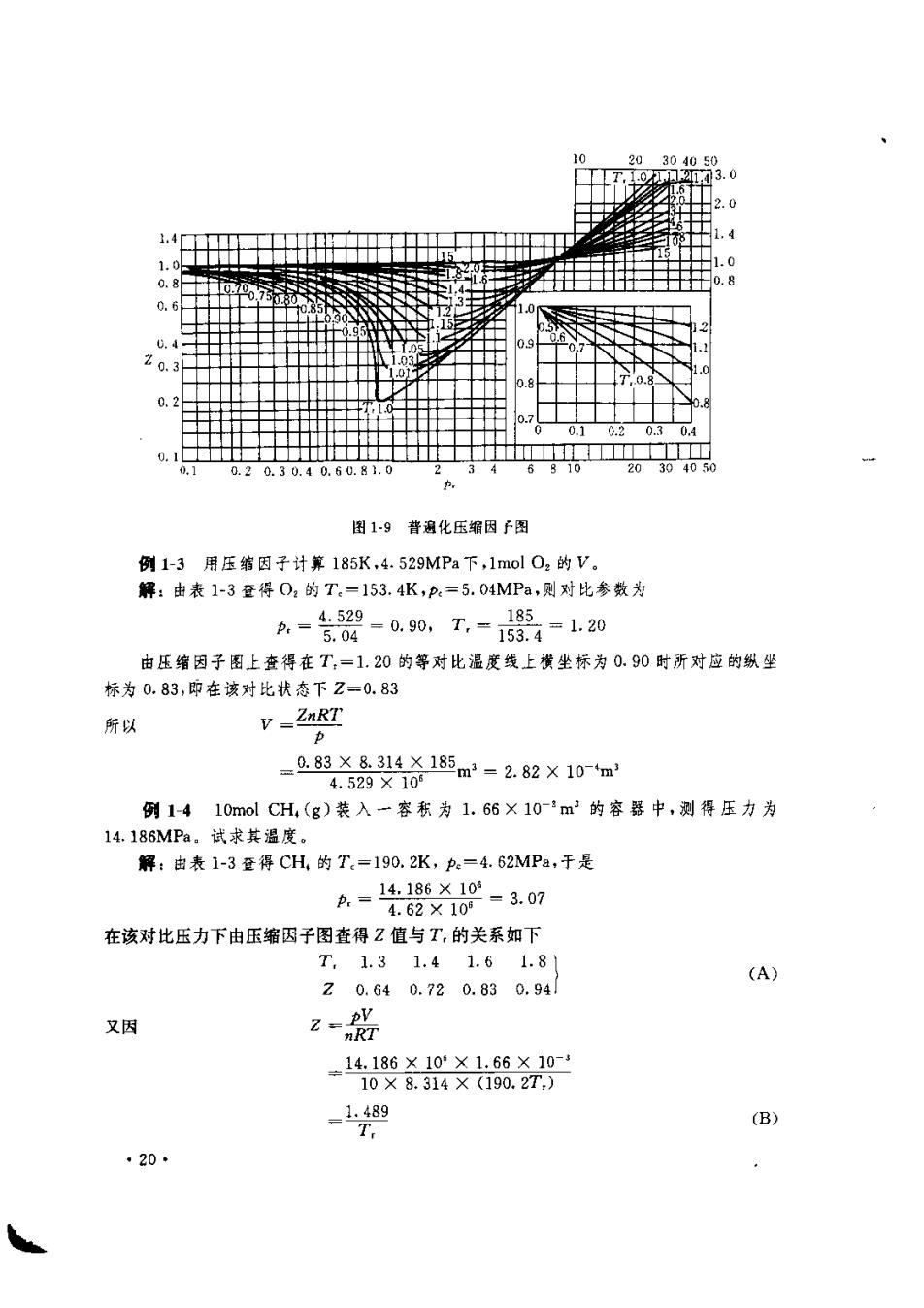
图1-9遍化压缩因图 例1-3用压缩因子计第185K,4.529MPa下,lmol02的V。 解:由表1-3查得02的T.-153.4K,p=5.04MPa,则对比参数为 A-股-0.90,T,-2=1.20 185 由压缩因子图上查得在T,-1.20的等对比温度线上横坐标为0.90时所对应的纵坐 标为0.83,即在该对比状态下Z=0.83 所以 V=ZnRT _0.83 例1-410 mol CH(g)装入一容积为1.66X10'm3的容器中,测得压力为 14.186MPa,试求其温度。 解:由表1-3查得CH,的T.=190.2K,=4.62MPa,于是 A.=14-186X0-3.07 4.62×10 在该对比压力下由压缩因子图查得Z值与T,的关系如下 T,1.31.41.6 1.8 (A) 20.640.720.830.94 又因 Z一R =1.489 (B) 20

可见Z与T,的关系既要满足关系(A),同时还要满足 关系式(B)。在坐标Z-T,上分别画出(A)和(B)所对应 的两条曲线,如图1-10所示。交点对应的T,即为题解 T=1.69 所以 T-TTe =1.69×190.2K =321K 例1-5已知CH,OH(g)的T.=513.1K,p 7.954MPa,今将1.104mol的气体装入一体积为8.00 X10m3的容器中,求当容器温度保持在623.2K时, 图1-10°例1-4图示 该气体的压力为若干? 解:T,=T/T.=623.2/531.1=1.21 甲醇气体的状态必在压缩因子图上T,=1.21的那条等对比温度线上,另外 即此气体的压缩因子与户,要满足Z=1.112p,因为此气体状态既要在T,=1.21等对比 温度线上同时又要满足关系Z=1.112。子是可在压缩因子图上画出直线Z=1.112力, 直线与T,-1.21曲线的交点所对应的,值为0.762。 所以 =P:Pe =0.762×7.954MPa-6.08MPa 此题也可用试差法求解。先设一压力值,求出,和T,由压缩因子图上查得相应的Z,便 可计算出V.将计算结果与实际体积比较,根据偏差情况,赋于压力新的数值,再重新计算 V值。照此办理,直到计算出的V值与实际体积相等为止。这也是工程上常用的方法。 由于对比状态原理是一个近似规律,所以用压缩因子图进行实际气体计算也只能得 到近似结果,但因为压缩因子图是在大量气体实验基础上得来的,因此与一般实际气体状 态方程相比,压缩因子图法的普适性较高。表1-5列出了在1.01325×10Pa时,用不同方 法计算出的N:的pVm/RT值。 表151.01325×10Pa时N,的登值 温度K 273.15 323.15 实脸伯 1.9285 按理想气体方程计算 十挥 1.00 -51.5 -48.1% 十 2.182 按Van der Waals方程i计算 2.426 17.6% 13.1% 计算值 2.10 1.95 用压缩因子图计算 误差 1.7% 1.1% 利用压缩因子图估算实际气体的性质是一种常用的简便方法,实践表明,压缩因子图 21·