
10Pa, 解:如果将气体作为理想气体处理,则 ==28.15p=s78×10pa 1.074> 与实验值的相对偏差为十14%。 由手册上查得CO,的Van der Waals常数a=o.364Pa·m·mol-,b- 4.27X10-m3·mol1.于是 p=-9 -0X027品1D-aX受p =5.02×10-8Pa 与实验值的相对偏差为一l.0%。由此可见,用Van der Waals方程计算出的结果远优于 理想气体状态方程 Van der Waals方程式可以写成 以.--品 根据式(1-6) [常21-x1 -[。-+员琴w-0 因为 所以 [。+员1-0 =- 于是 To -Rb (1-11) 每种气体都有各自的Boyle温度,但H,和He的Boyle温度远低于一般气体。由表 1-1可知,这是由它们的a值最低所致。气体的α催越大,分子间引力就起大,就越易于液 化,一般情况下具有较高的Boyle湿度 Van der Waals从理论上分析了实际气体与理想气体的区别,为实际气体建立了明 确的微观模型。对于处理实际气体做出了宝贵的贡献。实践证明,许多气体在中压范围内 (几百kPa到几千kPa)都能较好地服从Van der Waals方程。但如果气体压力很高,用此 方程会带来较大偏差。这主要是由于在方程的推证过程中,把α和b作为气体的物性参 数,对于指定的气体认为它们是不变的常数,这样处理过于粗糙。严格讲,和b与气体的 ◆12
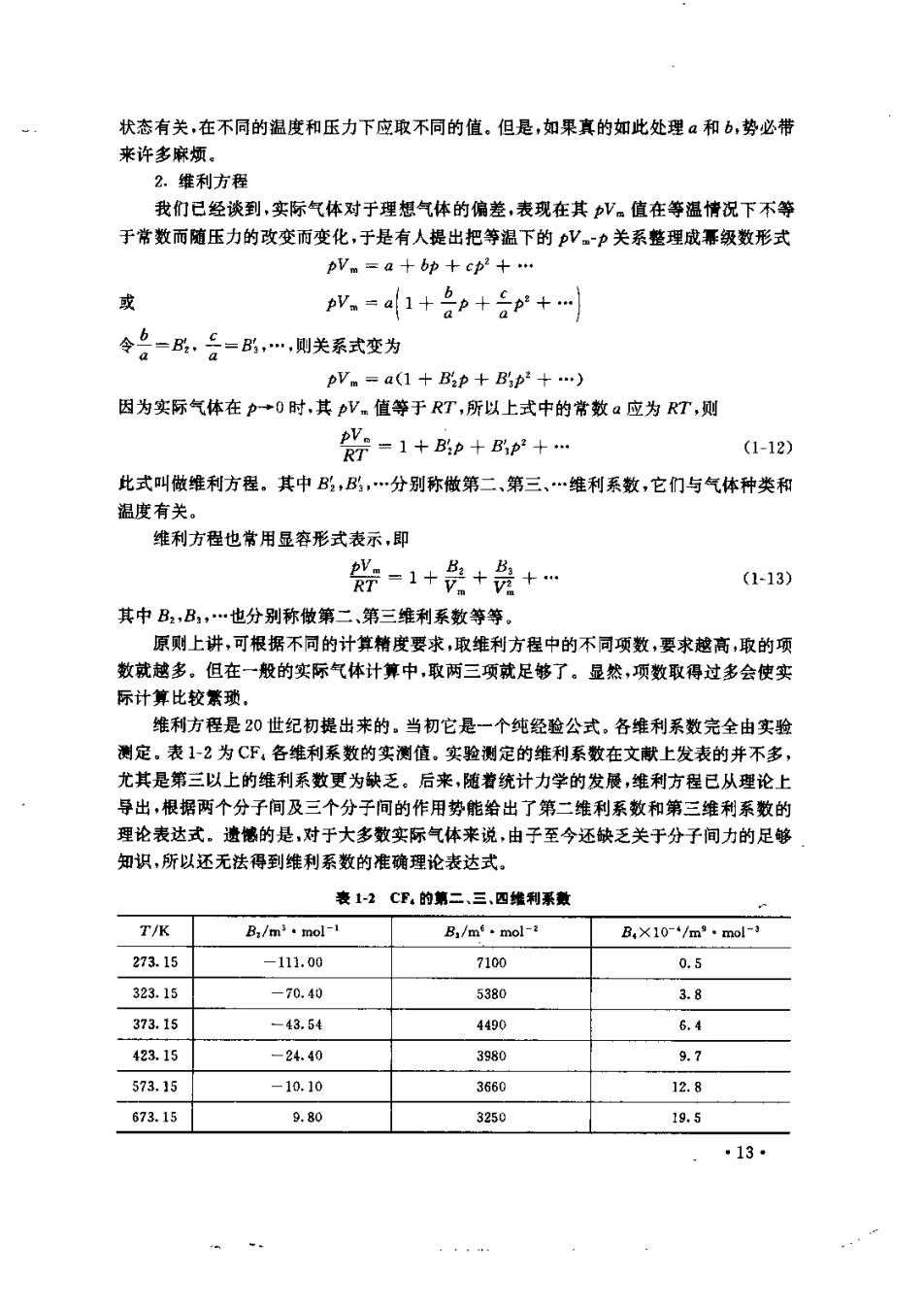
状态有关,在不同的温度和压力下应取不同的值。但是,如果真的如此处理和b,势必带 来许多麻烦。 2.维利方程 我们已经谈到,实际气体对于理想气体的偏整,表现在其V.值在等温情况下不等 于常数而随压力的改变而变化,于是有人提出把等温下的pV~p关系整理成幕级数形式 pVm=a十bp+cp2+… 或 v。=a1+p+ap+… 令名-品,台=…,则关系式变为 pVm=a(1十Bp+Bp2+…) 因为实际气体在p→0时,其pV.值等于RT,所以上式中的常数a应为RT,则 0=1+p+Bp+ (1-12) 此式叫做维利方程。其中,…分别称做第二、第三、…维利系数,它们与气体种类和 温度有关。 维利方程也常用显容形式表示,即 器-1+受+务+ (1-13) 其中B,B,…也分别称做第二、第三维利系数等等。 原则上讲,可根据不同的计算精度要求,取维利方程中的不同项数,要求越高,取的项 数就越多。但在一般的实际气体计算中,取两三项就足够了。显然,项数取得过多会使实 际计算比较素琐。 维利方程是20世纪初提出来的。当初它是一个纯经验公式。各维利系数完全由实验 测定。表1-2为C下,各维利系数的实测值,实验测定的维利系数在文款上发表的并不多, 尤其是第三以上的维利系数更为缺乏。后来,随着统计力学的发展,维利方程已从理论上 导出,根据两个分子间及三个分子间的作用势能给出了第二维利系数和第三维利系数的 理论表达式。遗够的是,对于大多数实际气体来说,由子至今还缺乏关于分子间力的足够 知识,所以还无法得到维利系数的准确理论表达式。 表1-2C里.的第二、三、四维利系数 T/K B/m.mol- B,/me·mol B.X10-+/m".mol-3 273.15 -112.00 7100 0.5 323.15 -70.40 5380 3.8 373.15 -43.54 4490 6.4 423.15 -24.40 3980 9.7 573.15 -10.10 3660 12.8 673.15 9.80 3250 19.5 13

3.其他状态方程 实际气体的状态方程常含有物性参数,例如Van der Waals方程中含a和b两个物 性参数。一般来讲,方程式中所含的物性参数越多,计算就越繁琐,但往往计算的精度起 高,普适性及适用的压力范围也越宽。随者计算机日益广泛的应用,人们已不再计较计算 工作量的大小,主要着眼于提高计算的精度。下面再介绍几个常用的状态方程: (I)R-K(RedIich-Kwong)方程 [p+v.w,46](W.-b)=RT (1-14) 其中,a和b为物性参数。它们的值与van der Waals数不同。R-K方程可在非常宽的 T,p范围内使用。 (2)Berthelot(贝塞罗)方程 (1-15) (3)Beattie(贝蒂)方程 V=a+1-)-导 (1-16) 式中 。=g日=B-名}=六A=A1-吕 其他类似的状态方程还有很多,其中有些确实具有各自的特点和长处但它们普遍的 问题是普适性不高,计算的精确度较差,有的甚至计算过于繁琐总之,至今尽管实际气体 的状态方程众多,但还没有哪一个让人们用起来得心应手,迫切需要普适性高,精确度高。 计算简单,使用方便的公式来满足实际生产和科学研究的器要 三、对比状态原理 1869年Andrew(安德鲁)通过实验研究了CO,气体的液化过程.将一定量的CO,气 体装入一个带有活塞的容器中,如图1-7所示,在一定沮度下,测量不同体积时容器内的 压力,然后再改变温度进行同样的测量,于是便得到各迅度下C0,的pV。等温线,如图 1-8所示,在较低的温度下,如286.25K,起初C0,气体的压力随体积压缩而逐浙增加,如 图中曲线HA。当压力增大到5,O66MPa时,容器中开始出现液态CO2,显然图中A点所 对应的体积是该温度时饱和CO,气体的摩尔体积。活塞继续缓慢下移,容器中的液态 CO2逐渐增加而气体逐渐减少,但容器的压力却保持5.O66MPa不变,直至B点C0,全 部变成液体为止,在图上形成水平直线AB。B点所对应的体积是该温度下饱和CO,液体 的摩尔体积。然后再继续压缩,则液态CO,的压力急剧升高,图上BM是一条很陡的曲 线,这反映了液体的难于压缩性。 水平直线AB上的每一个点都代表在286.25K时CO:液体和CO,气体共存的状态, 它们对应着同一个压力,即5.066MPa。人们把这个压力称做C0,在286.25K时的饱和 蒸气压。任何液体(甚至固体)都有饱和蒸气压,是指在一定条件下,能与液体平衡共存的 它的蒸气的压力,通常也称做蒸气压,燕气压是液体的属性,它代表液体气化的难易程度。 在指定温度下不同的液体相比,蒸气压越大,表明这种液体越容易挥发,同一种液体,其蒸 ·14
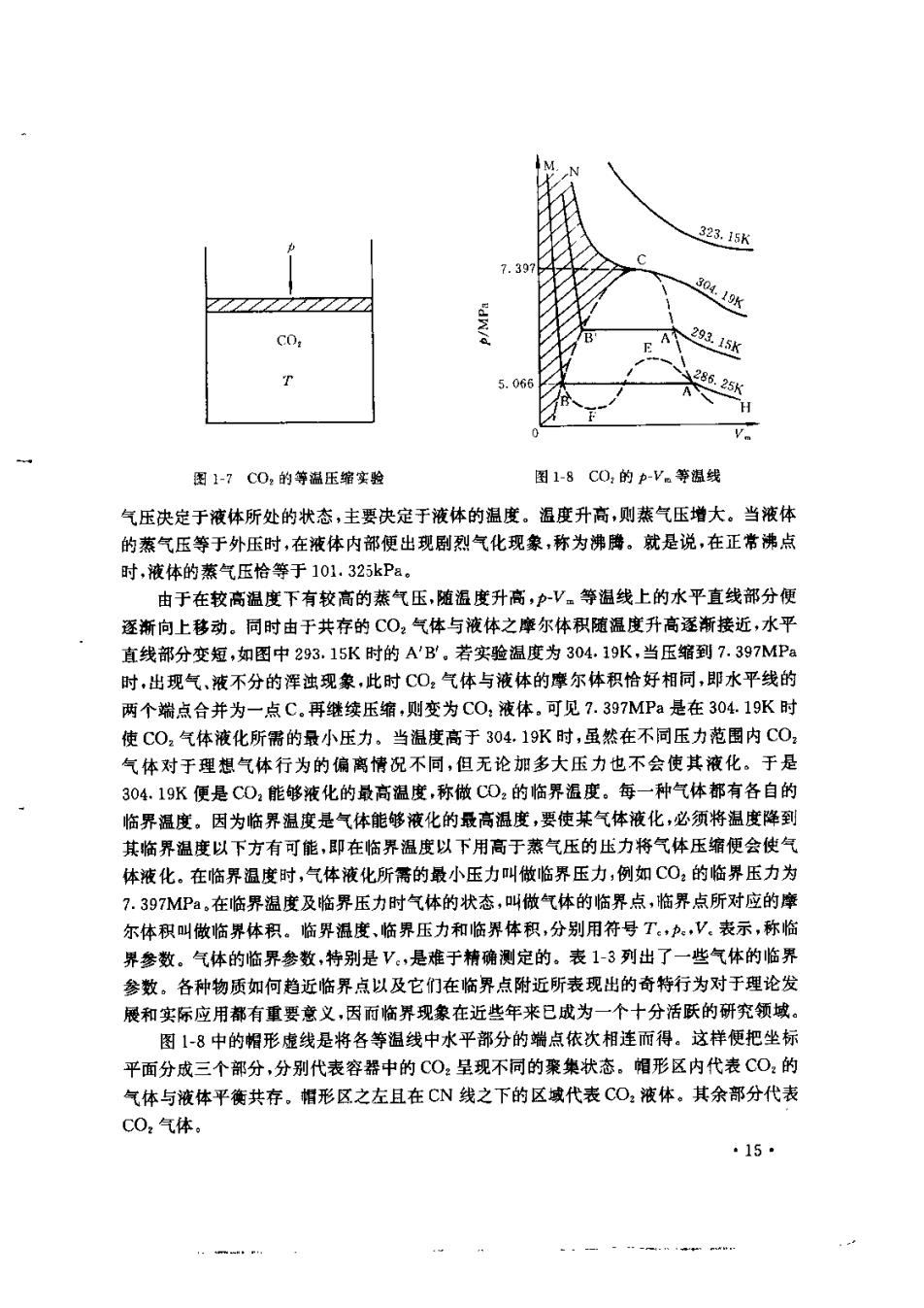
323.5K 7.39 30.19 293.15K 5.04 286.25K 图1-7C0,的等温压缩实验 图1-8C0,的p-V。等捆线 气压决定于液体所处的状态,主要决定于液体的温度。温度升高,则蒸气压增大。当液体 的蒸气压等于外压时,在液体内部便出现剧烈气化现象,称为沸腾。就是说,在正常沸点 时,液体的蒸气压恰等于101.325kPa 由于在较高温度下有较高的蒸气压,随温度升高,V。等温线上的水平直线部分便 逐渐向上移动。同时由于共存的CO,气体与液体之摩尔体积随温度升高逐渐接近,水平 直线部分变短,如图中293.15K时的A'B.若实验温度为304,19K,当压缩到7.397MP 时,出现气,液不分的浑浊现象,此时C0,气体与液体的摩尔体积恰好相同,即水平线的 两个端点合并为一点C.再继续压缩,则变为C0,液体,可见?.397MPa是在304.19K时 使C0,气体液化所需的最小压力,当温度高于304.19K时,虽然在不同压力范围内C0 气体对于理想气体行为的偏离情况不同,但无论加多大压力也不会使其液化。于是 304.19K便是CD,能够液化的最高温度,称做CD2的临界温度。每一种气体都有各自的 临界温度。因为临界温度是气体能够液化的最高温度,要使某气体液化,必须将温度降到 其临界温度以下方有可能,即在临界温度以下用高于蒸气压的压力将气体压缩便会使气 体液化。在临界温度时,气体液化所斋的最小压力叫做临界压力,例如CO,的临界压力为 7.397MPa,在临界温度及临界压力时气体的状态,叫做气体的临界点,临界点所对应的摩 尔体积叫做临界体积。临界温度,临界压力和临界体积,分别用符号T。,V。表示,称临 界叁数。气体的临界參数,特别是V,是难于精确测定的。表1-3列出了一些气体的临界 参数。各种物质如何趋近临界点以及它们在临界点附近所表现出的奇特行为对于理论发 展和实际应用都有重要意义,因而临界现象在近些年来已成为一个十分活跃的研究领域。 图18中的帽形虚线是将各等温线中水平部分的端点依次相连而得。这样便把坐标 平面分成三个部分,分别代表容器中的CO2呈现不同的聚集状态。帽形区内代表CO,的 气体与液体平衡共存。帽形区之左且在CN线之下的区域代表CO,液体。其余部分代表 C02气体。 15 m
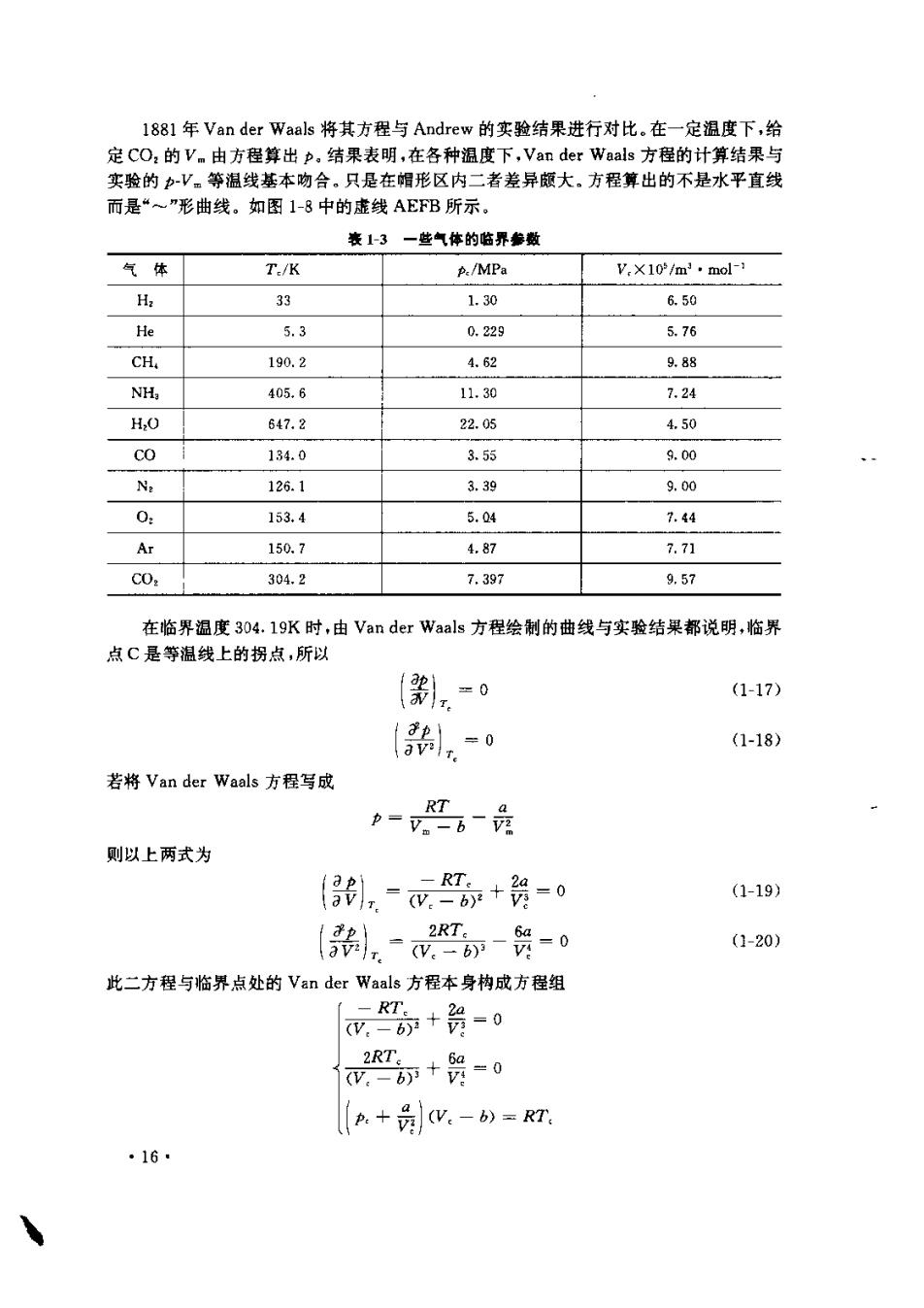
I88年Van der Waals将其方程与Andrew的实验结果进行对比.在一定温度下,给 定CO,的V.由方程算出p.结果表明,在各种温度下,Van der Waals方程的计算结果与 实验的PV等温线基本吻合。只是在帽形区内二者差异颇大。方程算出的不是水平直线 而是“~”形曲线。如图1-8中的虚线AEB所示 表13一些气体的临界参露 气体 T./K p./MPa V.X10/m3·mol-1 Ha 33 1.30 6.50 He 5.3 0.229 5.76 CH. 190,2 4.62 988 nh 405.6 11.30 7.24 H,0 647.2 22.05 4.50 CO 134.0 3.55 9.00 N: 126.1 3.39 9.00 0 153.4 5.04 7.44 Ar 150.7 4,87 7.71 C0. 304.2 7.397 9.57 在临界温度304.19K时,由Van der Waals方程绘制的曲线与实验结果都说明,临界 点C是等温线上的拐点,所以 器,=0 (1-17) 胎=0 (1-18) 若将Van der Waals方程写成 =网员 则以上两式为 0,-.+贺-0 -RT. (1-19) 员-0 (1-20 此二方程与临界点处的Van der Waals方程本身构成方程组 +员-0 ,-衍+哭-0 2RT. p.+号W.-b)=RT ·16·