
R=2=Jno1K- =8.314J·mol1,K- 在一毅温度下,分子总器不停地以很高的速摩无规则地运动着,同时分千之间存在差 相互作用,在通常情况下这种相互作用表现为相互吸引.固体和液体的分子会聚巢在一起 而不一个一个地分散开就是这种引力存在的有力证据。 气体之所以与固体和液体不同,能充满整个容器,是因为 气体分子间的引力很小,不足以抗衡分子的无规侧云动 分子之间不仅表现为吸引力,有时也表现为排斥力。图 1-2为分子间力f与分子闻距离,的关系曲线。可以看 出,当分子间距离<。(r,约在10~1m左右)时,分子间 力表现为斥力,并且随者r的诚小,斥力急剧增加,当 千力 r>r,时,分子间力表现为引力。超过A点之后,r越大则 引力小.我们知道,理想气体状态方程代表着实际气体 压力趋于零时的极限情况。气体的压力趋于零就意味着 图12分子间力与分子间 其体积无穷大,此时必有以下两个结论:①分子间距离 距离的关系 ©0,因此分子间没有相互作用:②分子本身所占的体 积与气体所占的无穷大体积相比可以忽略不计,即分子是没有体积的质点。于是,从微观 上讲,理想气体是分子之间没有相互作用且分子没有大小的气体.这就是理想气体的微观 特征。 二、分压定律 在日常的科学研究及生产活动中,遇到的气体绝大部分是气体混合物,在一个气体混 合物中,任意组分气体B的分压定义为 pa一xB力 (1-3) 式中x是混合气中气体B的物质的量分数(摩尔分数),P是混合气的压力,即混合气的 总压。于是,对子一个由种气体构成的气体混合物,则 p十p:+ …十p=(知十x十…十x)书 金 ∑Pe=p (1-4) 这就是说,在气体混合物中,所有组分气体的分压之和等于混合气的总压。所以可把分压 看作组分气体B对总压的贡献。 若构成混合气的种气体均是理想气体,而且混合气仍服从理想气体状态方程,则此 混合气称为理想气体混合物。设温度T时,某体积为V的刚体容器中,装有理想气体混合 物,混合气的总压为,物质的量为,则 p=nRT/V 将此式代入式(1-3),得 *74
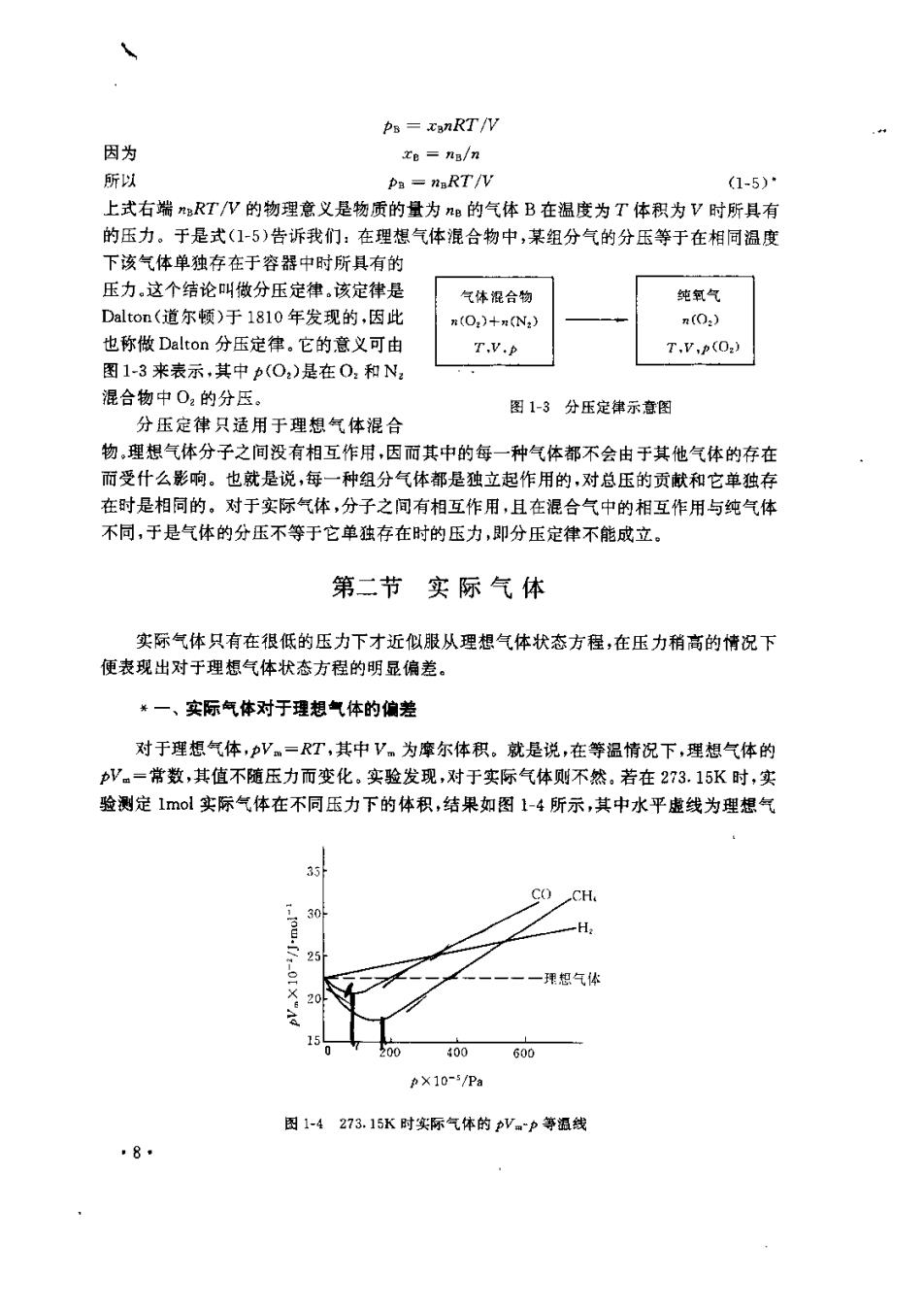
Ps=xsnRT/V 因为 te nB/n 所以 Pa-naRT/V (1-5) 上式右端RT八的物理意义是物质的量为m的气体B在温度为T体积为V时所具有 的压力。于是式(15)告诉我们:在理想气体混合物中,某组分气的分压等于在相同温度 下该气体单独存在于容器中时所具有的 压力。这个结论叫做分压定律,该定律是 气体混合物 纯氧气 Dalton(道尔顿)于1810年发现的,因此 n(O:)+n(N:) n(0:) 也称做Dalton分压定律,它的意义可由 T,v,(0) 图1-3来表示,其中p(O)是在0,和N 混合物中02的分压。 图1-3分压定律示查图 分压定律只造用于理想气体混合 物,理想气体分子之间没有相互作用,因而其中的每一种气体都不会由于其他气体的存在 而受什么影响。也就是说,每一种组分气体都是独立起作用的,对总压的贡献和它单独存 在时是相同的。对于实际气体,分子之间有相互作用,且在混合气中的相互作用与纯气体 不同,于是气体的分压不等于它单独存在时的压力,即分压定律不能成立。 第二节实际气体 实际气体只有在很低的压力下才近似服从理想气体状态方程,在压力稍高的情况下 便表现出对于理想气体状态方程的明显偏差。 一、实际气体对于理想气体的偏差 对于理想气体,pV。=RT,其中V,为摩尔体积。就是说,在等温情况下,理想气体的 V==常数,其值不随压力而变化。实验发现,对于实际气体则不然,若在273.15K时,实 验测定1ol实际气体在不同压力下的体积,结果如图-4所示,其中水平虚线为理想气 CH 0 H 一理您气体 400 600 pX10-5/P3 图1-4273.15K时实际气体的pV。p等祖线 8
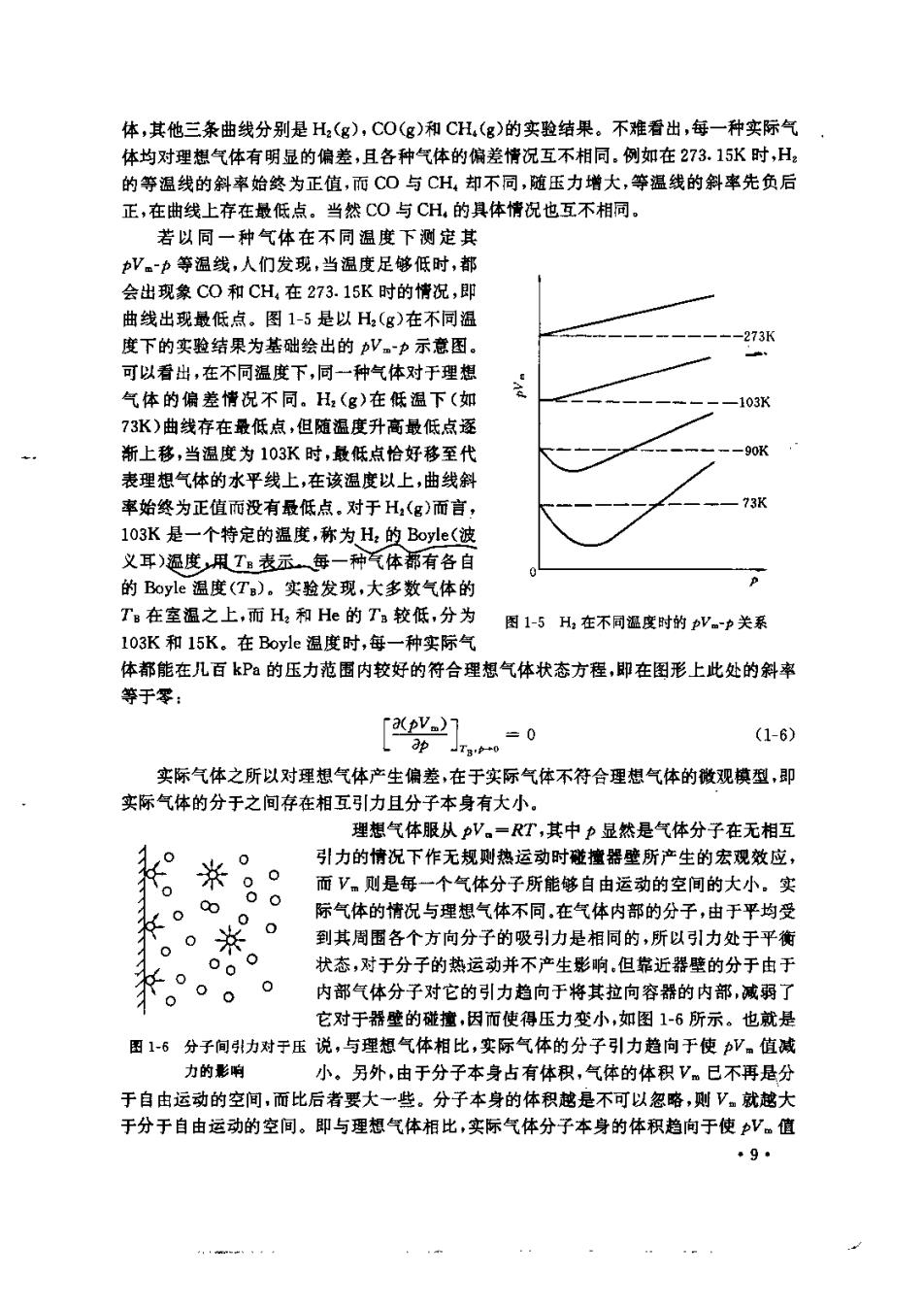
体,其他三条曲线分别是H,(g),C0(g)和CH(g)的实验结果。不难看出,每一种实际气 体均对理想气体有明显的偏差,且各种气体的偏差情况互不相同,例如在273.15水时,H 的等温线的斜率始终为正值,而C0与CH,却不同,随玉力增大,等温线的斜率先负后 正,在曲线上存在最低点。当然CO与CH,的具体情况也互不相同, 若以同一种气体在不同温度下测定其 V。p等温线,人们发现,当温度足够低时,都 会出现象C0和CH在273.15K时的情况,那 曲线出现最低点。图1-5是以H,(g)在不同温 度下的实验结果为基础绘出的V。力示意图。 73H 可以看出,在不同温度下,同一种气体对于理巷 气体的偏差情况不同。H2(g)在低温下(如 73K)曲线存在最低点,但随温度升高最低点逐 断上移,当祖度为103K时,最低点恰好移至代 表理想气体的水平线上,在该温度以上,曲线斜 率始终为正值而没有最低点,对于H,(g)而言, 103K是一个特定的温度,称为H,的Bole(波 义耳)度凡T表示每一种气体都有各自 的Boyle温度(T),实验发现,大多数气体的 T在室温之上,而H2和He的T较低,分为 图1-5H,在不同温度时的pV。p关系 103K和15K.在Bovle福度时,每一种实际气 体都能在几百kP的压力范围内较好的符合理想气体状态方程,即在图形上此处的斜率 等于零: 0 (1-6) 实际气体之所以对理想气体产生偏差,在于实际气体不符合理想气体的微观模型,即 实际气体的分于之间存在相互引力且分子本身有大小 理想气体服从pV。=RT,其中p显然是气体分子在无相互 。 并。 引力的情况下作无规则热运动时碰撞器壁所产生的宏观效应, 而V。则是每一个气体分子所能够自由运动的空间的大小。实 。 际气体的情况与理想气体不同,在气体内部的分子,由于平均受 到其周围各个方向分子的吸引力是相同的,所以引力处于平衡 0.0 状态,对于分子的热运动并不产生影响,但靠近器壁的分于由于 0 内部气体分子对它的引力趋向于将其拉向容器的内部,减弱了 它对于器壁的碰撞,因而使得压力变小,如图1-6所示。也就是 图1-6分子间力对于压说,与理想气体相比,实际气体的分子引力趋向于使。值减 力的影响 小。另外,由于分子本身占有体积,气体的体积Vm已不再是分 于自由运动的空间,而比后者要大一些。分子本身的体积越是不可以忽略,则V。就越大 于分于自由运动的空间。即与理想气体相比,实际气体分子本身的体积趋向于使V。值 。9

增大。可见,实际气体的分子引力效应和分子体积效应对于V。是两个相反的影响因素 在某一确定的温度和压力下,某气体对于理想气体的偏差情况如何,即实际的V,值比 理相的大环是小,取快于这两个因素的相对强弱。当T<T时,在低压范围内,贿压力增 大两种效应均要增强,但由于分子引力效应是矛盾的主要方面,致使随压力升高。值 减小。当压力增大到一定程度,矛盾双方发生转化,分子的体积效应变成矛盾的主要方面, 于是随压力升高Ψ值增大。当压力增大到某一个值时,两种效应势均力敌,相互抵消 表现为V。=T,这就是V。~中图中曲线与水平虚线的交点.当T>T时,分子体积效应 总是强于分子引力效应,因而始终表现为V。随压力升高而增大。 二、实际气体的状态方程 在工业生产中,实际气体的状态方程往往比理想气体状态方程有更高的实用价值。因 此,长期以来人们一直在为寻找裤意的实际气体状态方程而努力。到目前为止,这样的方 程已经提出近200个,大体可分为两类:①半理论半经验性的,这一类考虑到分子的相互 引力和分子的大小、具有一定的物理模型,但由此推导出的状态方程中的某些参量仍需要 通过实验夹测定;②纯经验性的。这一类是通过部分气体的实验结果归纳出来的。它 只适用于那些用于实验的特定气体,工业上这类方程为数众多。 1.Van der Waals(范德华)方程 荷兰科学家Van der Waals根据实际气体的具体情况,对理想气体状态方程进行了 修正,于1373年提出了Van der Waals方程他的基本思想是,实际气体的分子引力效应 使其压力变小,藏小值称为内压,如果将内压加到气体的实测压力上即得到当分子间 无引力时气体所应具有的压力,即(中+)为理想气体的压力,由于实际气体分子有大小, 所以从气体的体积V(即容器的容积)中扣除分于本身所占据的体积b,便得到气体分子 自由运动的空间,即(W。一h)可视为理想气体的体积。需要说明,严格讲b并不等于1mol 气体分子本身所占有的体积,而是分子相互碰撞时,分子间的斥力所排除的体积。而液体 中分子是紧密连在一起的,所以b粗略的等于液体的摩尔体积。于是通过以上两项措施便 修正了实际气体的两个不理想效应,即 (b+b.)(V.-b)-=RT (1.7) 内压是由子分子间引力而产生的,所以它一方面与气体内部分子数N成正比, 另一方面又与碰渔器壁的分子数N。成正比,即 pcNN 而N和N。都正比于气体的密度P,所以 1mol气体的密度p与体积成反比,子是 户心园 即 办一觉 (1-8) 式中4为比例常数。将上式代入式(1-7)得 ·10
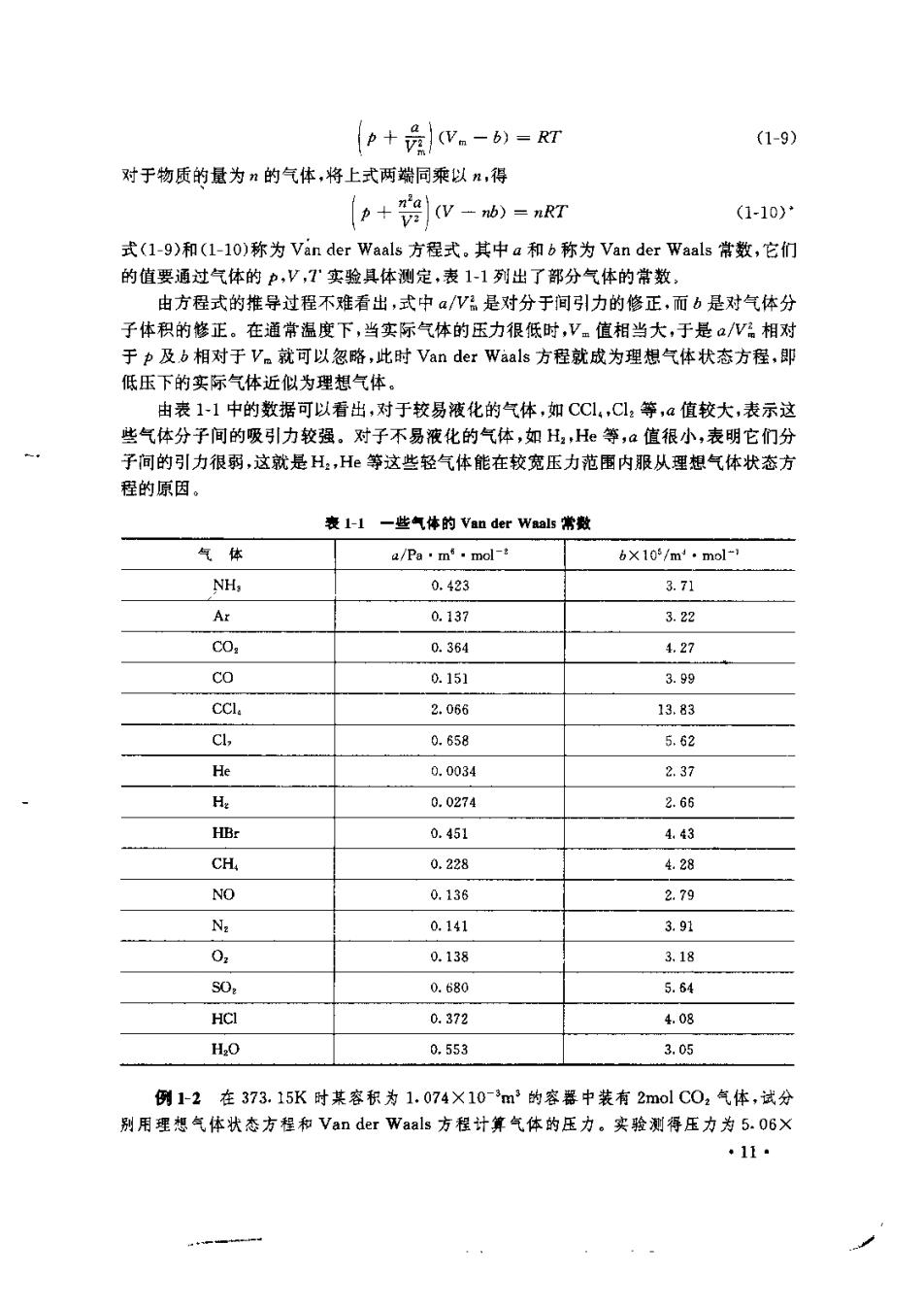
p+员(V。-b)=RI (1-9) 对于物质的危为n的气体,将上式两端同乘以”,得 ((V-n)-nRT (1-10) 式(1-9)和(1-l0)称为Vin der Waals方程式.其中a和b称为Van der Waals常数,它们 的值要通过气体的p,V,T实验具体测定,表11列出了部分气体的常数, 由方程式的推导过程不难看出,式中a/W品是对分于间引力的修正,而b是对气体分 子体积的修正。在通常温度下,当实际气体的压力很低时,V。值相当大,于是aW相对 于中及b相对于V。就可以忽略,此时Van der Waals方程就成为理想气体状态方程,即 低压下的实际气体近似为理想气体。 由表1-1中的数据可以看出,对于较易液化的气体,如CCl,Cl:等,@值较大,表示这 些气体分子间的吸引力较强。对子不易液化的气体,如H2,H等,a值很小,表明它们分 子间的引力很弱,这就是H:,H等这些轻气体能在较宽压力范围内服从理想气体状态方 程的原因。 表1-H一些气体的Van der Waals常数 气体 a/Pa·m·molt 6X103/m·mol- NH, 0.423 3.71 Ar 0.137 322 c0, 0.364 4.27 co 0.151 3.99 cCl. 2.086 13.83 Cl, 0.658 5.62 He 0.0034 237 0.0274 2.66 HBr 0.451 4,43 CH 0.228 4.28 NO 0.136 2.79 0.141 3.91 02 0.138 3.18 50: 0.680 5.64 HCI 0.372 4.08 H20 0.553 3.05 例1-2在373.15K时某容积为1.074×10-3m3的容器中装有2molC0,气体,试分 别用理想气体状态方程和Van der Waals方程计算气体的压力。实验测得压力为5.06× 11