
第三部分信号的处理和分析 广东工业大学机电工程学院 例设有两个周期信号x()和y() xt)=x,sin(ot+O) y(t)=yo sin (@t+0-p 试求其互相关函数R(x) 解:因为函数是周期信号,可以用一个共同周期内的平 均值代替其整个历程的平均值,故 R,()=7x)+)d in()sin(d xy%cos(ot-p) 此例可知,两个同频率的信号,其互相关函数保留了 圆频率、幅值、及相位差值信息
第三部分 信号的处理和分析 广东工业大学机电工程学院 解: 因为函数是周期信号,可以用一个共同周期内的平 均值代替其整个历程的平均值,故 0 0 0 0 0 0 1 lim 1 sin sin 1 cos 2 T xy T T R x t y t d t T x t t dt T x y 此例可知,两个同频率的信号,其互相关函数保留了 圆频率、幅值、及相位差值信息 tyty txtx sin sin 0 0 例 设有两个周期信号x(t) 和y (t) 。试求其互相关函数 Rxy

第三部分信号的处理和分析广东工业大学机电工程学院 例若两个周期信号的圆频率不等 试求其互相关函数 xd)=xsm(o,t+0) y(t)=yosin (@t+0-p 解:因为两信号不具有共同的周期,所以有 R()(+) so-0sito.(+r) lim 根据正余弦函数的正交性,可知 R(a)=0
第三部分 信号的处理和分析 广东工业大学机电工程学院 例 若两个周期信号的圆频率不等 试求其互相关函数 tyty txtx 0 2 0 1 sin sin 解:因为两信号不具有共同的周期,所以有 T T T T xy tyx t dt T tytx dt T R 0 00 1 2 0 0 sin sin 1 lim 1 lim 根据正余弦函数的正交性,可知 0 Rxy

第三部分信号的处理和分析广东工业大学机电工程学院 3.应用 1)测试系统的滞后时间; 2)相关滤波:应用相关分析来滤除信号中的噪声干扰、提 取有用信息的处理方法。 3)广泛地应用于各种测试中。 案例1:地下输油管道漏损位置的探测 S=-(vot)/2 互相关分析 中心线 x1(t) x2(t) 油 传感器1 传感器2 破损处
第三部分 信号的处理和分析 广东工业大学机电工程学院 案例 1:地下输油管道漏损位置的探测 3. 应用 1)测试系统的滞后时间; 2)相关滤波:应用相关分析来滤除信号中的噪声干扰、提 取有用信息的处理方法。 3)广泛地应用于各种测试中。 S=(v 0 τ)/2
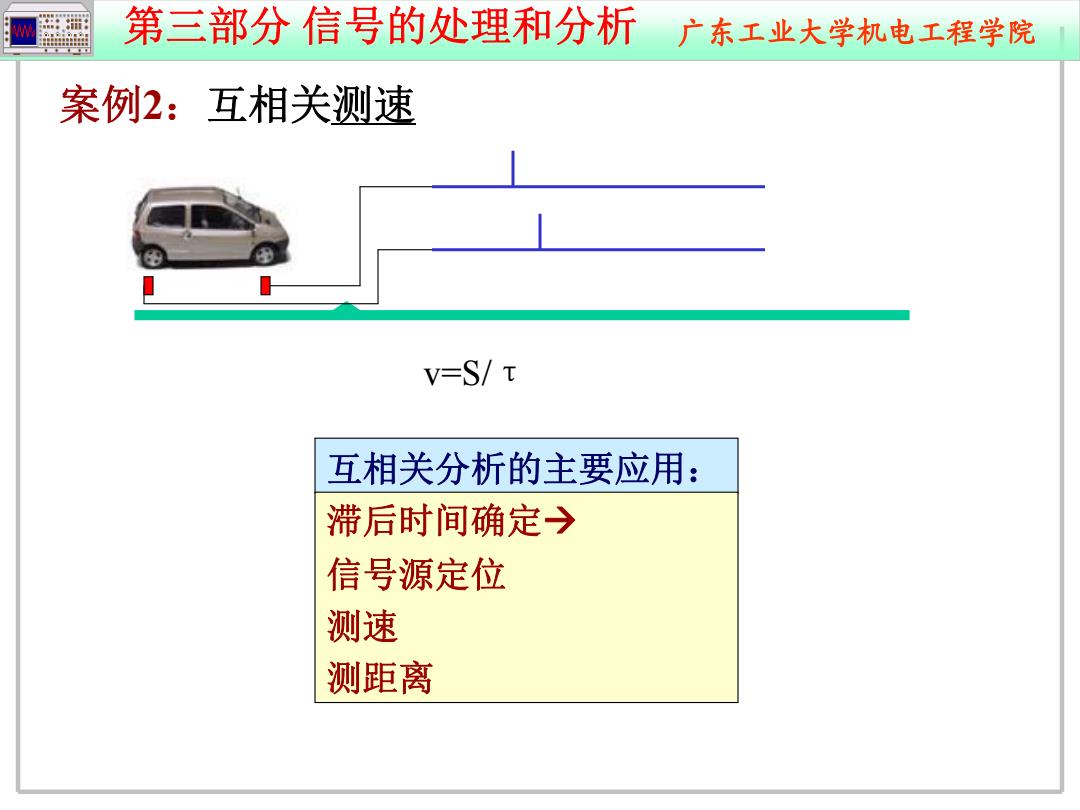
第三部分信号的处理和分析广东工业大学机电工程学院 案例2:互相关测速 v=S/t 互相关分析的主要应用: 滞后时间确定→ 信号源定位 测速 测距离
第三部分 信号的处理和分析 广东工业大学机电工程学院 案例 2 :互相关测速 互相关分析的主要应用: 滞后时间确定 信号源定位 测速 测距离 v=S/ τ

第三部分信号的处理和分析 广东工业大学机电工程学院 3.5信号的功率谱分析 3.5.1 自功率谱密度函数—相关函数的富里叶变换 1.定义:又称自谱密度函数或自谱 S,()=R,(ce rdr 闭=m子 x(t)y(t+r)dt 2.物理意义:是信号的功率沿频率轴的分 布,描述了信号功率随频率变化的分布关系
第三部分 信号的处理和分析 广东工业大学机电工程学院 3.5 信号的功率谱分析 3.5.1 自功率谱密度函数——相关函数的富里叶变换 2.物理意义 :是信号的功率沿频率轴的分 布,描述了信号功率随频率变化的分布关系 2 ( ) () j f x x S f Re d 1.定义:又称自谱密度函数或自谱 0 1 ( ) lim ( ) ( ) T xy T R x t y t dt T