
Signaling Games ● Signaling Requirement 3:For each m;in M,If there exists t;in T such that m*(t)=m;,then the Receiver's belief at the information set corresponding to m;must follow from Bayes rule and the Sender's strategy: (|m)= p4) p4) t,∈T Definition:A pure-strategy perfect Bayesian equilibrium is a signaling game is a pair of strategies m*(f)and a*(m) and a belief u(tm)satisfying Signaling Requirements (1),(2R),(2S),and(3) 16
Signaling Games • Signaling Requirement 3: For each mj in M, If there exists t i in T such that m*(t i )=mj , then the Receiver’s belief at the information set corresponding to mj must follow from Bayes’ rule and the Sender’s strategy: • Definition: A pure-strategy perfect Bayesian equilibrium is a signaling game is a pair of strategies m*(t i ) and a*(mj ) and a belief μ(t i |mj ) satisfying Signaling Requirements (1),(2R),(2S), and (3) ( ) ( | ) ( ) i i i j i t T p t t m p t = 16
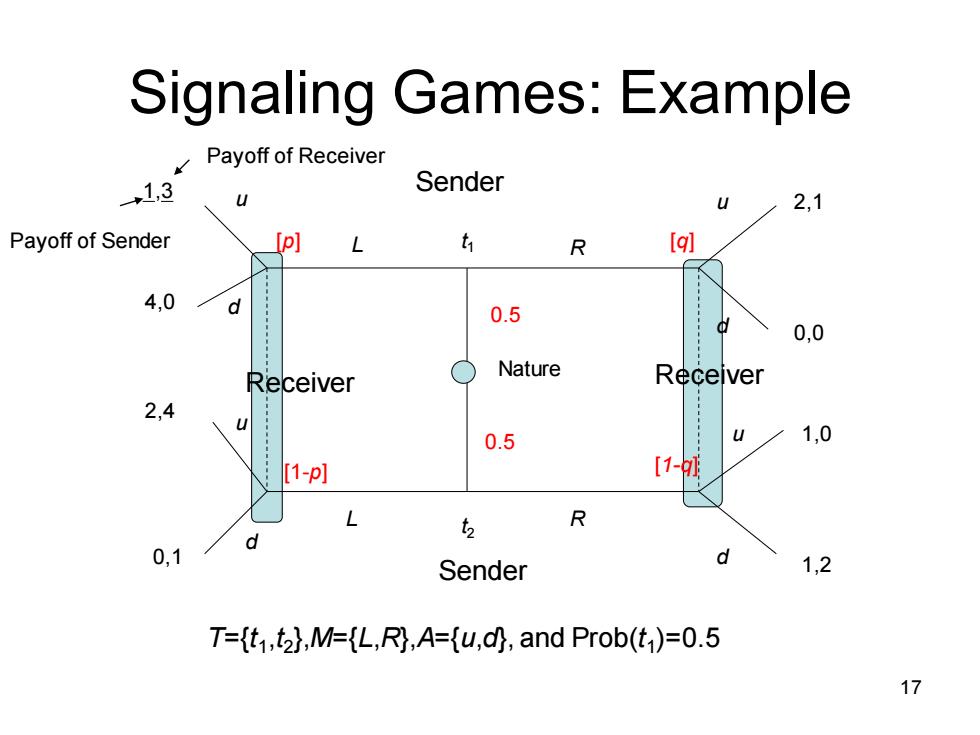
Signaling Games:Example Payoff of Receiver →1,3 Sender 2,1 Payoff of Sender [p] t R [ql 4,0 a 0.5 d 0,0 Receiver Nature Receiver 2,4 0.5 1,0 [1-p] [1-叫 t R 0,1 Sender 1,2 T=(t,t2),M=(L,R),A=(u,d),and Prob(t )=0.5 17
Signaling Games: Example u d u d L R L R u d d u Nature 0.5 0.5 t1 t2 Sender Sender Receiver Receiver T={t1 ,t2 },M={L,R},A={u,d}, and Prob(t1 )=0.5 1,3 4,0 2,4 0,1 2,1 0,0 1,0 1,2 [p] [1-p] [q] [1-q] Payoff of Sender Payoff of Receiver 17

Signaling Games Type t Type t2 ·Approach Given the Sender's strategy (m(t),m(t2)),derive the receiver's optimal strategy (a(L),a(R)) Signal L Signal R Given receiver's strategy,check whether the Sender's strategy is optimal 18
Signaling Games • Approach – Given the Sender’s strategy (m(t1 ), m(t2 )), derive the receiver’s optimal strategy (a(L), a(R)) – Given receiver’s strategy, check whether the Sender’s strategy is optimal Type t1 Type t2 Signal L Signal R 18

Signaling Games The Sender's strategy Strategy 1:m(t)=L and m(t2)=L(pooling) The Receiver's strategy:a(L)=u and a(R)=d,p=0.5,q<=2/3(PBE) If a(R)=u,then type f Sender will deviate to play R Condition for a(R)=d is g.0+(1-q).2>=q.1+(1-q).0 Strategy 2:m(t)=L and m(t2)=R(separating) The Receiver's strategy:p=1,q=0,a(L)=u and a(R)=d No equilibrium(the type f2 Sender will deviate to play L) Strategy 3:m(t)=R and m(t2)=L(separating) The Receiver's strategy:p=0,q=1,a(L)=u and a(R)=u,(PBE) Strategy 4:m(t)=R and m(t2)=R(pooling) The Receiver's strategy:q=0.5,a(R)=d,for all p,a(L)=u 0.5x0+0.5x2(play d)>0.5x1+0.5x0(play u) No equilibrium(the typet Sender will deviate to play L) 19
Signaling Games The Sender’s strategy – Strategy 1: m(t1 )=L and m(t2 )=L (pooling) • The Receiver’s strategy: a(L)=u and a(R)=d, p=0.5, q<=2/3 (PBE) • If a(R)=u, then type t1Sender will deviate to play R • Condition for a(R)=d is q.0+(1-q).2>=q.1+(1-q).0 – Strategy 2: m(t1 )=L and m(t2 )=R (separating) • The Receiver’s strategy: p=1, q=0, a(L)=u and a(R)=d • No equilibrium (the type t2 Sender will deviate to play L ) – Strategy 3: m(t1 )=R and m(t2 )=L (separating) • The Receiver’s strategy: p=0,q=1, a(L)=u and a(R)=u, (PBE) – Strategy 4: m(t1 )=R and m(t2 )=R (pooling) • The Receiver’s strategy: q=0.5, a(R)=d , for all p, a(L)=u 0.5x0+0.5x2 (play d)>0.5x1+0.5x0 (play u) • No equilibrium (the type t1 Sender will deviate to play L) 19