
Perfect Bayesian Equilibrium(cont') Requirement 3(Belief based on Bayes rule):At the information sets on the equilibrium path,beliefs are determined by Bayes'rule and the players'equilibrium strategies Requirement 4(Reasonable belief):At the information sets off the equilibrium path,beliefs are determined by Bayes'rule and the players equilibrium strategies where possible Definition:A perfect Bayesian equilibrium consists of strategies and beliefs satisfying requirement 1 through 4 6
Perfect Bayesian Equilibrium (cont’) • Requirement 3 (Belief based on Bayes’ rule): At the information sets on the equilibrium path, beliefs are determined by Bayes’ rule and the players’ equilibrium strategies • Requirement 4 (Reasonable belief): At the information sets off the equilibrium path, beliefs are determined by Bayes’ rule and the players’ equilibrium strategies where possible • Definition: A perfect Bayesian equilibrium consists of strategies and beliefs satisfying requirement 1 through 4 6
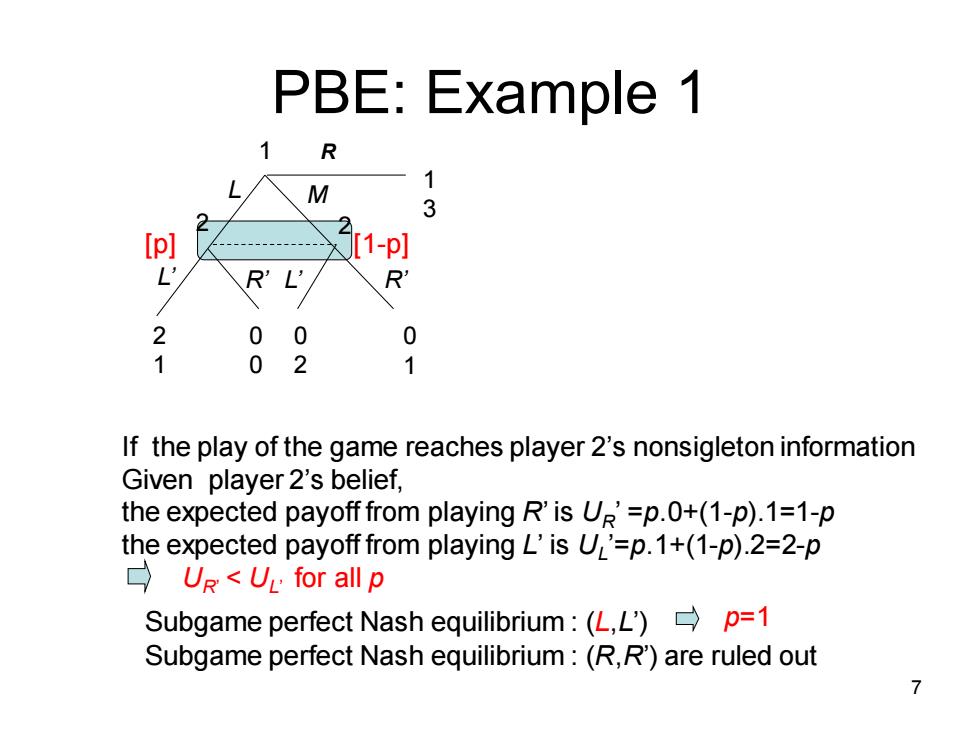
PBE:Example 1 R 1 M 3 2 1-p R 0 0 0 0 2 1 If the play of the game reaches player 2's nonsigleton information Given player 2's belief, the expected payoff from playing R'is UR=p.0+(1-p).1=1-p the expected payoff from playing L'is UL'=p.1+(1-p).2=2-p UR<UL:for all p Subgame perfect Nash equilibrium:(L,L')p=1 Subgame perfect Nash equilibrium:(R,R)are ruled out 7
PBE: Example 1 2 2 2 1 0 0 0 2 0 1 L M L’ R’ L’ R’ 1 1 3 R Subgame perfect Nash equilibrium : (L,L’) [p] [1-p] p=1 If the play of the game reaches player 2’s nonsigleton information Given player 2’s belief, the expected payoff from playing R’ is UR’ =p.0+(1-p).1=1-p the expected payoff from playing L’ is UL ’=p.1+(1-p).2=2-p UR’ < UL’ for all p Subgame perfect Nash equilibrium : (R,R’) are ruled out 7
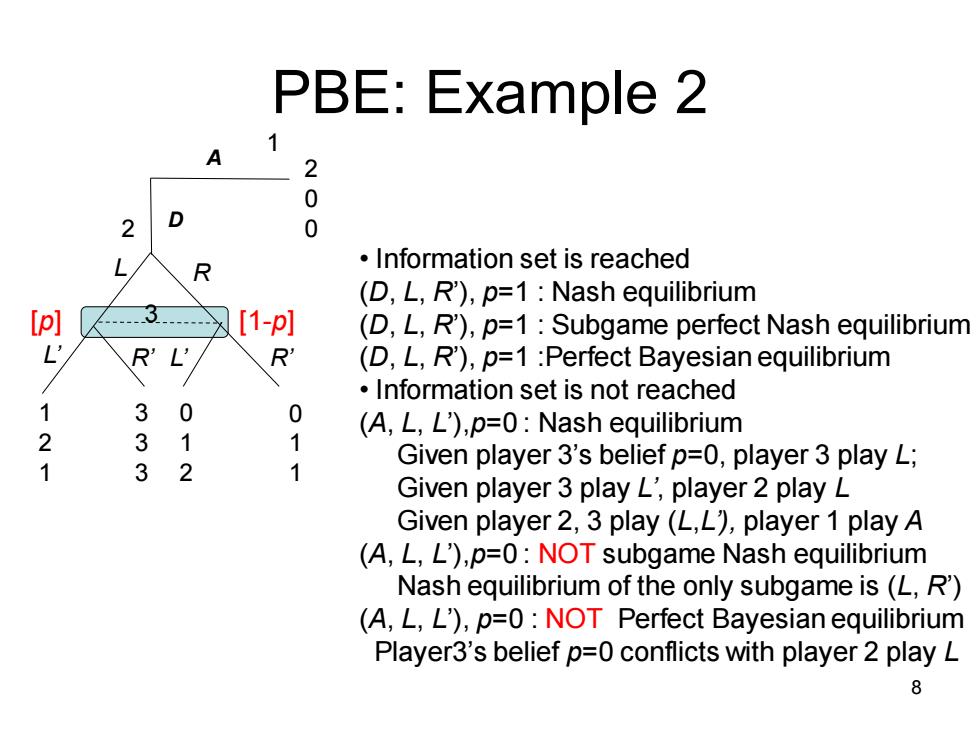
PBE:Example 2 1 2 0 2 D 0 L R Information set is reached (D,L,R'),p=1 Nash equilibrium [p] [1-p] (D,L,R'),p=1 Subgame perfect Nash equilibrium R (D,L,R),p=1 Perfect Bayesian equilibrium Information set is not reached 3 0 0 (A,L,L'),p=0:Nash equilibrium 2 3 1 3 2 1 Given player 3's belief p=0,player 3 play L; Given player 3 play L',player 2 play L Given player 2,3 play(L,L),player 1 play A (A,L,L'),p=0:NOT subgame Nash equilibrium Nash equilibrium of the only subgame is(L,R) (A,L,L'),p=0:NOT Perfect Bayesian equilibrium Player3's belief p=0 conflicts with player 2 play L 8
PBE: Example 2 3 1 2 1 3 3 3 0 1 2 0 1 1 L R L’ R’ L’ R’ 2 D [p] [1-p] A 1 2 0 0 • Information set is reached (D, L, R’), p=1 : Nash equilibrium (D, L, R’), p=1 : Subgame perfect Nash equilibrium (D, L, R’), p=1 :Perfect Bayesian equilibrium • Information set is not reached (A, L, L’),p=0 : Nash equilibrium Given player 3’s belief p=0, player 3 play L; Given player 3 play L’, player 2 play L Given player 2, 3 play (L,L’), player 1 play A (A, L, L’),p=0 : NOT subgame Nash equilibrium Nash equilibrium of the only subgame is (L, R’) (A, L, L’), p=0 : NOT Perfect Bayesian equilibrium Player3’s belief p=0 conflicts with player 2 play L 8

PBE:Example 3 1.If player 1's equilibrium strategy is A,requirement 4 may not determine 3's belief from player 2 strategy(the player 3's information set is off equilibrium path) D 2.If player 2's strategy is A'then requirement 4 puts 2 no restrictions on 3's belief(the player 3's R information set is off equilibrium path) 3.If 2's strategy is to play L with probability q,R [p] [1-p] with probability q2,and A'with probability 1-q-q2, R then requirement 4 dictates that 3's belief be p=q/(q+q2)(the player 3's information set is on equilibrium path) 9
PBE: Example 3 3 L R L’ R’ L’ R’ 2 D [p] [1-p] 1 A A’ 1. If player 1’s equilibrium strategy is A, requirement 4 may not determine 3’s belief from player 2 strategy (the player 3 ‘s information set is off equilibrium path) 2. If player 2’s strategy is A’ then requirement 4 puts no restrictions on 3’s belief (the player 3 ‘s information set is off equilibrium path) 3. If 2’s strategy is to play L with probability q1 , R with probability q2 , and A’ with probability 1-q1 -q2 , then requirement 4 dictates that 3’s belief be p=q1 /(q1+q2 ) (the player 3 ‘s information set is on equilibrium path) 9

Signaling Games A signaling game is a dynamic game of incomplete information involving two players:a Sender (S)and a Receiver (R) 。 Timing of the game is as follows: -1.Nature draws a type f;for the Sender from a set of feasible types T={f,...,t according to a probability distribution p(t), where p(t)>0 for every i and p(f)+...+p(t)=1 -2.The Sender observes t;and then chooses a message m;from a set of feasible M=tm,...,.m 3.The Receiver observes m;(but not t)and then chooses an action ak from a set of feasible actions A={a,...,a -4.Payoffs are given by Us(ti,miak)and UR(ti.mj,ak) 10
Signaling Games • A signaling game is a dynamic game of incomplete information involving two players: a Sender (S) and a Receiver (R) • Timing of the game is as follows: – 1. Nature draws a type t i for the Sender from a set of feasible types T={t1 ,…,t I } according to a probability distribution p(t i ), where p(t i )>0 for every i and p(t1 )+…+p(t I )=1 – 2. The Sender observes t i and then chooses a message mj from a set of feasible M={m1 ,…,. mJ } – 3. The Receiver observes mj (but not t i ) and then chooses an action ak from a set of feasible actions A={a1 ,…,aK} – 4.Payoffs are given by US (t i ,mj ,ak ) and UR(t i,mj ,ak ) 10