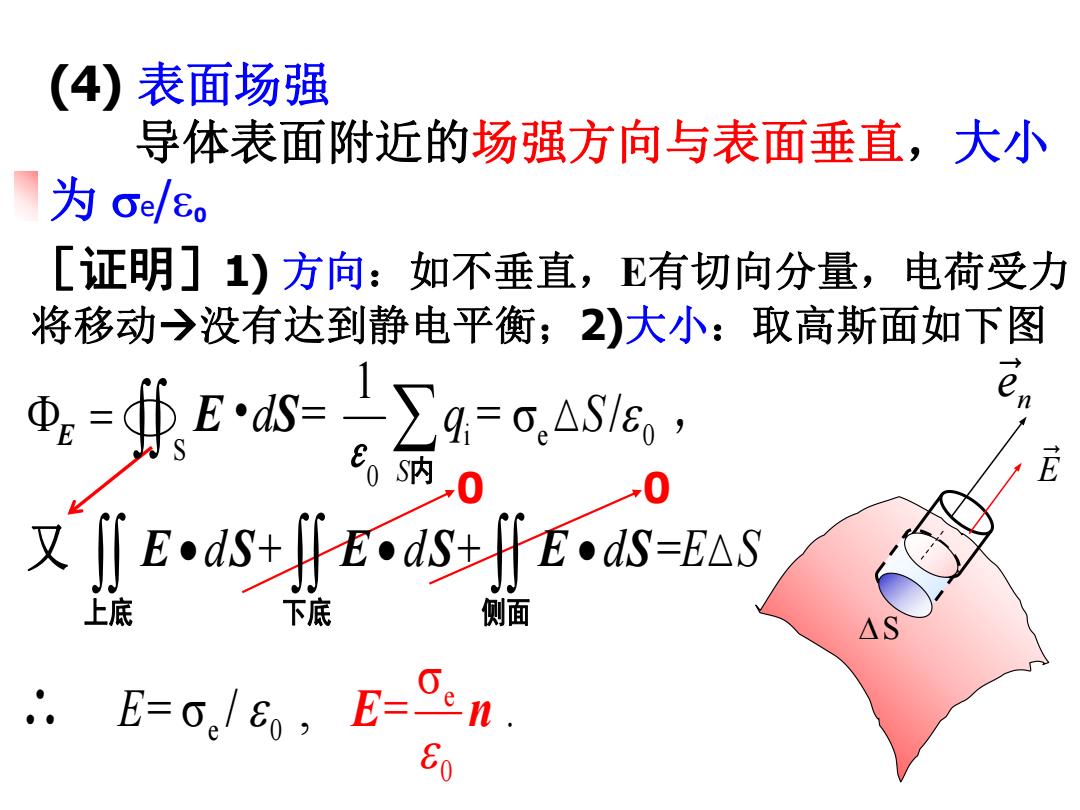
(4)表面场强 导体表面附近的场强方向与表面垂直,大小 为e/o [证明]1)方向:如不垂直,E有切向分量,电荷受力 将移动→没有达到静电平衡;2)大小:取高斯面如下图 =∯ES=。∑q=o,△S6, .0 又∬Ed5+Eds-fE.ds=-faS 上底 下底 侧面 E=。/,E= n
(4) 表面场强 导体表面附近的场强方向与表面垂直,大小 为 e/0 [证明]1) 方向:如不垂直,E有切向分量,电荷受力 将移动没有达到静电平衡;2)大小:取高斯面如下图 S n e r 0 0 e 0 i e 0 S 0 e 0 1 = = / + + = = / , = . S d q S d d d E S E E Ò E S , E S E S E E n S • ∴ 又 内 上底 下底 侧面 ε E r
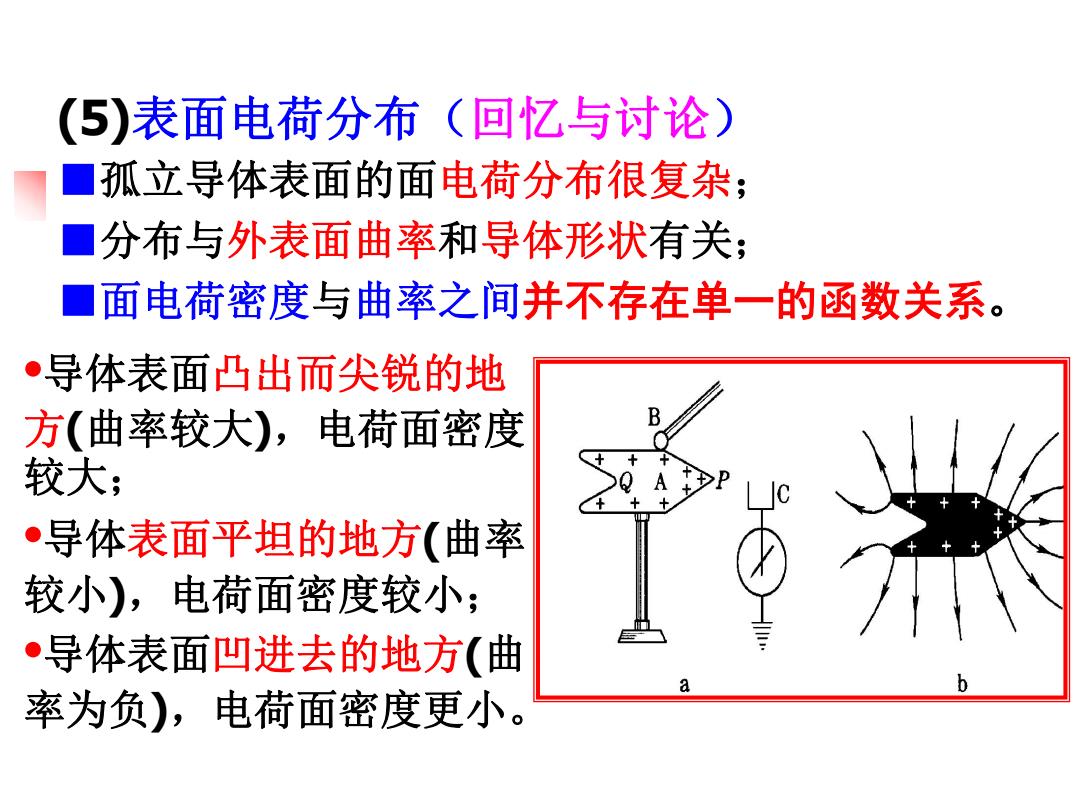
(5)表面电荷分布(回忆与讨论) 孤立导体表面的面电荷分布很复杂; ■分布与外表面曲率和导体形状有关; ■面电荷密度与曲率之间并不存在单一的函数关系。 ●导体表面凸出而尖锐的地 方(曲率较大),电荷面密度 较大; ·导体表面平坦的地方(曲率 较小),电荷面密度较小: ·导体表面凹进去的地方(曲 a b 率为负),电荷面密度更小
(5)表面电荷分布(回忆与讨论) ■孤立导体表面的面电荷分布很复杂; ■分布与外表面曲率和导体形状有关; ■面电荷密度与曲率之间并不存在单一的函数关系。 •导体表面凸出而尖锐的地 方(曲率较大),电荷面密度 较大; •导体表面平坦的地方(曲率 较小),电荷面密度较小; •导体表面凹进去的地方(曲 率为负),电荷面密度更小

[例]半径分别为R和r(R>r)导体球放置在相距无限远的 两个地方,中间用细导线连接。导体球分别带电Q和q, 求两球表面电荷面密度与曲率的关系。(思考题) [解]两个导体所组成的整体可看成是 一个孤立导体系,U相等,每个球可近似 的看作为孤立导体,球表面电荷分布均 匀,则两球的电势为: IR=Ur= 19 4π6R 4π80r R R 4πR'o= R 4π26, R 电荷面密度与半径成反比 R
[例]半径分别为R和r (R>r)导体球放置在相距无限远的 两个地方,中间用细导线连接。导体球分别带电Q和q, 求两球表面电荷面密度与曲率的关系。(思考题) [解] 两个导体所组成的整体可看成是 一个孤立导体系,U相等,每个球可近似 的看作为孤立导体,球表面电荷分布均 匀,则两球的电势为: R r Q q 0 0 2 2 1 1 , 4 4 4 , , 4 . R r R r R r Q q U U R r Q R R R q r r r r R 电荷面密度与半径成反比

讨论题: 设无穷远处电势U∞=0,与仪器的外 壳接地的电势U地=0是否相容?
讨论题: 设无穷远处电势U=0,与仪器的外 壳接地的电势U地 =0 是否相容?

3.导体在静电场中性质的应用(演示2.2-2.7) 尖端放电 曲率大,oe大,E=eJ大 避雷针 静电复印机 场致发射显微镜 范德格拉夫起电机 静电屏蔽空腔导体可以保护腔内空间不受腔 外带电体的影响 屏蔽室 带电作业 范德格拉夫起电机 库仑定律的精确验证 b
3. 导体在静电场中性质的应用(演示2.2-2.7) n 尖端放电 曲率大,e大,E = e /0 大 n 避雷针 n 静电复印机 n 场致发射显微镜 n 范德格拉夫起电机 n 静电屏蔽 空腔导体可以保护腔内空间不受腔 外带电体的影响 n 屏蔽室 n 带电作业 n 范德格拉夫起电机 n 库仑定律的精确验证