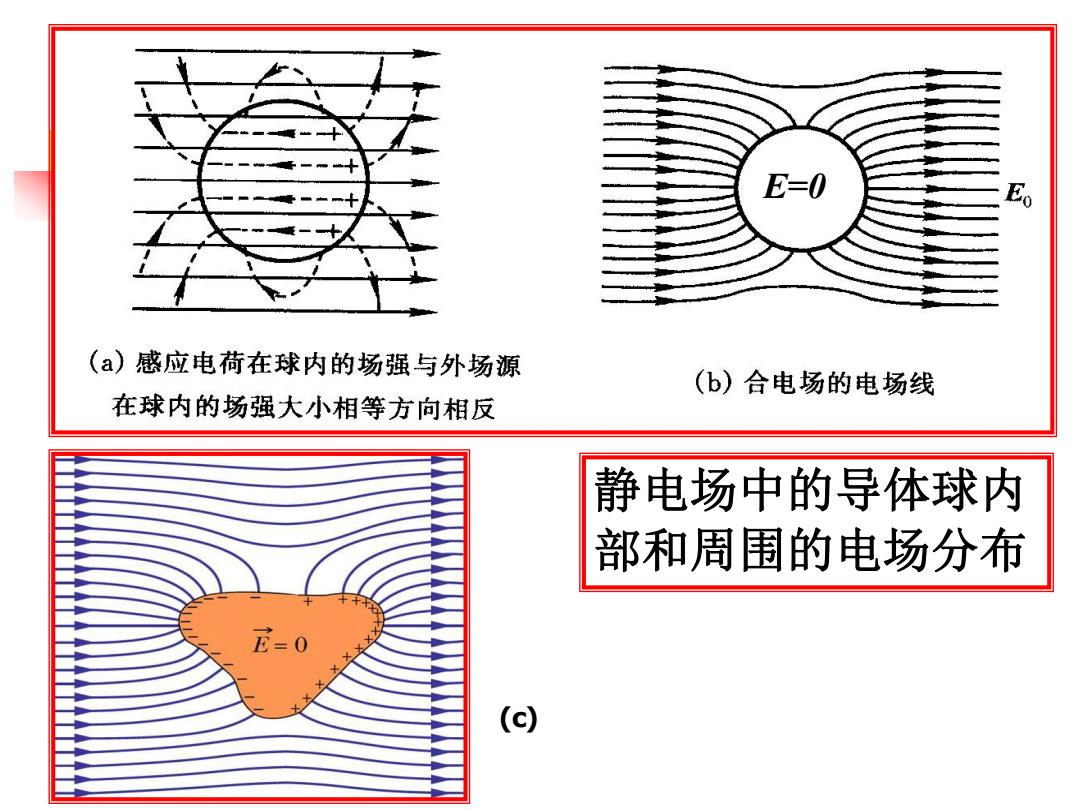
E=0 Eo (a)感应电荷在球内的场强与外场源 (b)合电场的电场线 在球内的场强大小相等方向相反 静电场中的导体球内 部和周围的电场分布 元=0 (c)
静电场中的导体球内 部和周围的电场分布 (c) E=0
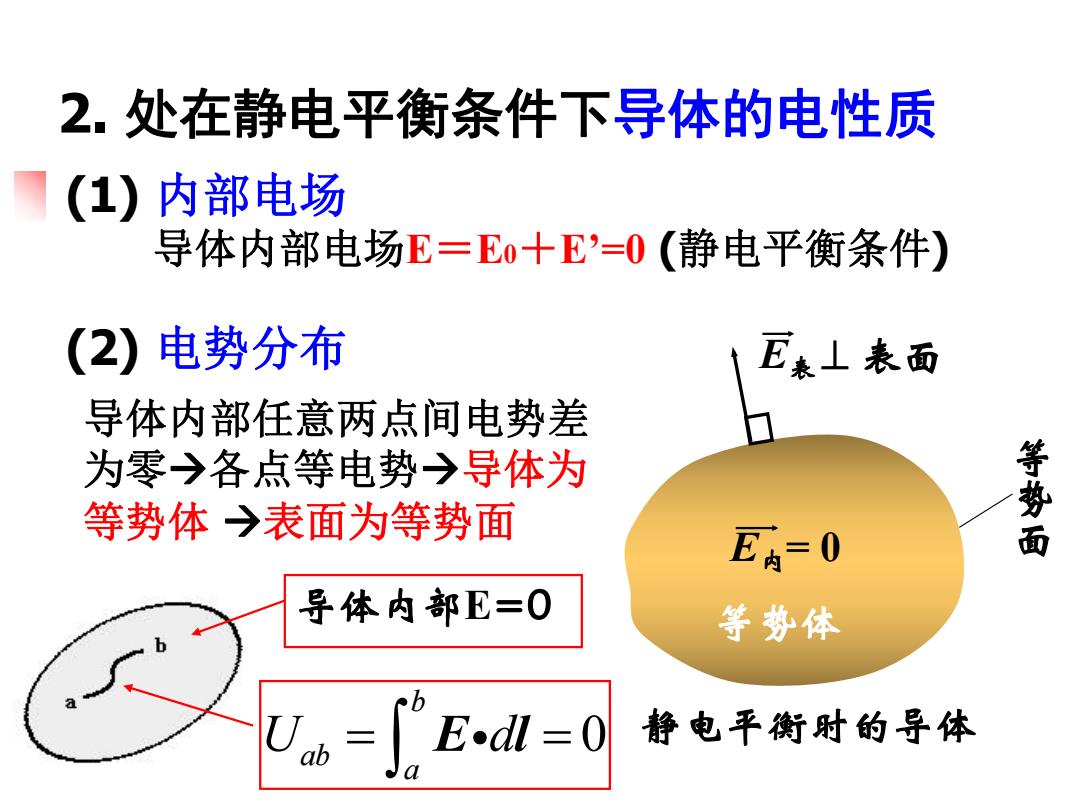
2.处在静电平衡条件下导体的电性质 (1)内部电场 导体内部电场E=E0+E'=0(静电平衡条件) (2)电势分布 E表上表面 导体内部任意两点间电势差 为零→各点等电势→导体为 等势体→表面为等势面 E内=0 等势面 导体内部E=0 等势体 )ab =Edl=0 静电平衡时的导体
2. 处在静电平衡条件下导体的电性质 (1) 内部电场 导体内部电场E=E0+E’=0 (静电平衡条件) E内= 0 静电平衡时的导体 等势体 E表 等 势 面 (2) 电势分布 表面 导体内部E=0 0 b ab a U d Eg l 导体内部任意两点间电势差 为零各点等电势导体为 等势体 表面为等势面

(3)整体电荷分布 实心导体:■当带电导体处于静电平衡状态时,导体内 部处处没有净电荷存在,电荷密度处处为零pe=0。 ■电荷只分布在导体表面。导体表面电荷 的电荷层一般只有1至2个原子的厚度。 【证明】:在导体内任取体积元dW,再 取任一闭合曲面S包围它,由高斯定理: &∯FS=∑4, :E±0,∴∑9=Jj川p.aW=0, .·体积元dW任取,即V任取 ∴.p。=0
(3) 整体电荷分布 实心导体: ■当带电导体处于静电平衡状态时,导体内 部处处没有净电荷存在,电荷密度处处为零ρe=0。 ■电荷只分布在导体表面。导体表面电荷 的电荷层一般只有1至2个原子的厚度。 【证明】:在导体内任取体积元dV,再 取任一闭合曲面S包围它,由高斯定理: 0 , 0, 0. 0. i S i i e V i e d q q dV V dV 体积元 任取,即 任取 E S Q E Q Ò dV S

导体空腔(腔内没有带电体情况) 包围导体空腔的导体壳内表面上处处没有电荷,电荷 分布在导体外表面,空腔内处处E=0,空腔内处处电势 相等。 【证明】在导体中包围空腔选取高斯面S, 则: fwds-o.fods-0 若0内≠0,则0丙必有正负, 便有E线从正电荷到负电荷 外 导体内表面出现了电势差。 这与导体为等势体矛盾, E 只能O内=0,且腔内无E线。 ·E为=0今AU=El=0
导体空腔(腔内没有带电体情况) ■ 包围导体空腔的导体壳内表面上处处没有电荷,电荷 分布在导体外表面,空腔内处处E=0,空腔内处处电势 相等。 d 0, S E导内 QÒ s S 【证明】在导体中包围空腔选取高斯面S, 则: d 0 S S 内 Ò 内 , 若内 0,则内必有正负, 便有E线从正电荷到负电荷, 导体内表面出现了电势差。 只能内 =0,且腔内无E线。 ∵ E内 = 0 这与导体为等势体矛盾,∴ 0. b a U d Eg l 0
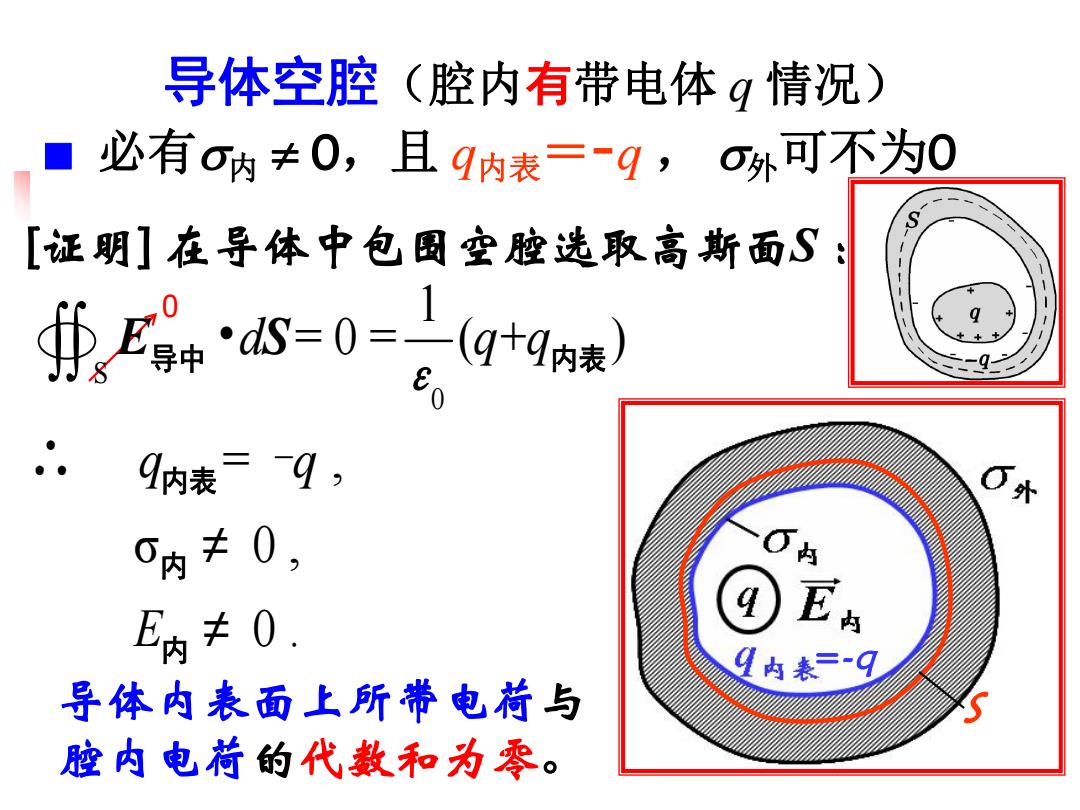
导体空腔(腔内有带电体q情况) 必有O内≠0,且q内表=-q,O外可不为0 [证明]在导体中包围空腔选取高斯面S ∯E写中·aS=0=。(g+9g装 9内表=9, 6* 0内0, 内 E内≠0. 9内表=-9 导体内表面上所带电荷与 腔内电荷的代数和为零
导体空腔(腔内有带电体 q 情况) ■ 必有内 0,且 q内表= ̵q , 外可不为0 [证明] 在导体中包围空腔选取高斯面S : S =-q 导体内表面上所带电荷与 腔内电荷的代数和为零。 0 S 0 1 = 0 = ( + ) = , σ 0 , 0 . d q q q q E Ò E • S ∴ – ≠ ≠ 导中 内表 内表 内 内 ε