
[例2.2] 右下图所示的电偶极子由一对相距 为1的等量异号电荷±q构成,两个电荷的位置 分别为r,相应电偶极矩为p=ql=9心-r) 求该电偶极子在外场E中所受的力F及所受的 力矩L。 [解]设在”与 处的外电场强度分 别为E和E2,则有 F=gE2-gE =gE(r)-gE(r)
[例2.2 ] 右下图所示的电偶极子由一对相距 为l 的等量异号电荷 构成,两个电荷的位置 分别为 ,相应电偶极矩为 。 求该电偶极子在外场E 中所受的力F 及所受的 力矩 L 。 q r q q( ) p l r r [解] 设在 与 处的外电场强度分 别为E1和E2,则有 r r 2 1 q q q ( ) q ( ). F E E E r E r

■设r为原点到电偶极子中点的矢径,且1<r 则由泰勒展开取头两项得(难点!) F=q[E(+1/2)-E(r-112]≈q(L:V)E(r) r=(r+1/2)=(x+△x/2,y+△y2,2+△z/2) ◆即 F=(p.V)E(r) (2.1.4) ■在外电场中受的力矩L(以电偶极子中点为参 考点):L=-)xg6,-)×g5≈g×E 即 L=p×E (2.1.5) 在推导中,近似取:E1=E2=E(中点处电场)
■设r 为原点到电偶极子中点的矢径,且 , 则由泰勒展开取头两项得(难点!) l r F q[E(r l / 2) E(r l / 2)] q(l )E(r) 即 F ( p )E (r) (2.1.4) ■在外电场中受的力矩L(以电偶极子中点为参 考点): 2 1 L(r r)qE (r r)qE ql E 即 L p E (2.1.5) 在推导中,近似取: E1 = E2 = E (中点处电场) . r+ =(r l / 2)= x x / 2, y y / 2, z z / 2

§2.2静电场中的导体 导体达到静电平衡的条件 导体的特点是体内有自由的戴流子,静电场 会改变导体内电荷的分布电荷分布的改 变将影响电场的分布>使得导体内电场强 度处处为零,则自由电荷不再运动我们 说导体达到静电平衡 这时导体内自由电荷分布以及导体内、外的 电场分布不再随时间变化。这个过程进行得 很快,大约在108-10-10 sec就完成了
§2.2 静电场中的导体 1. 导体达到静电平衡的条件 ■ 导体的特点是体内有自由的戴流子,静电场 会改变导体内电荷的分布 电荷分布的改 变将影响电场的分布 使得导体内电场强 度处处为零,则自由电荷不再运动 我们 说导体达到静电平衡。 ■ 这时导体内自由电荷分布以及导体内、外的 电场分布不再随时间变化。 这个过程进行得 很快,大约在 10 8 10 10 sec就完成了

对于不存在非静电力情况下的均匀、 各向同性导体,达到静电平衡的条件 是导体内部电场强度处处为零。 以上所采用的是演绎法!即从基本定律 出发,通过逻辑推理,得到导体达到静电 平衡的条件
■ 对于不存在非静电力情况下的均匀、 各向同性导体,达到静电平衡的条件 是导体内部电场强度处处为零。 以上所采用的是演绎法!即从基本定律 出发,通过逻辑推理,得到导体达到静电 平衡的条件
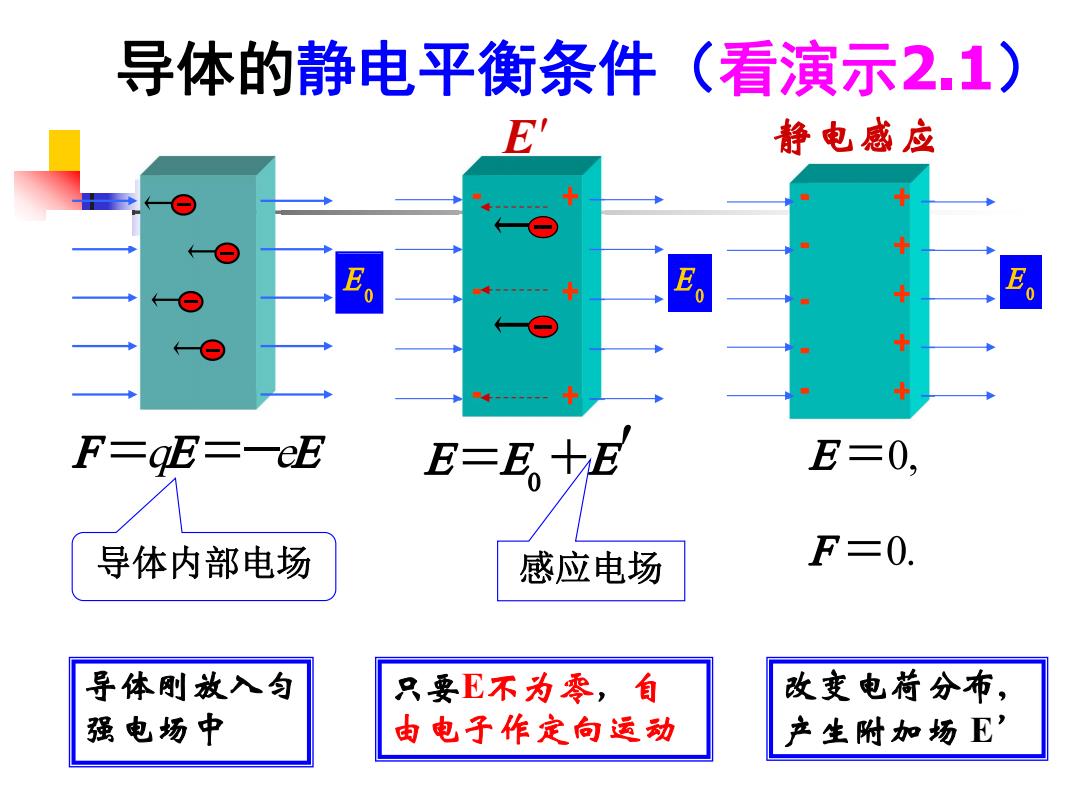
导体的静电平衡条件(看演示2.1) E' 静电感应 0 0 F=gE=一eE E-EE E=0, 导体内部电场 感应电场 F=0. 导体则放入匀 只要E不为零,自 改变电荷分布, 强电场中 由电子作定向运动 产生附加场E
0 E 0 E E E 0 E 0, 0. E F 0 E E 静电感应 导体的静电平衡条件(看演示2.1) 导体刚放入匀 强电场中 只要E不为零,自 由电子作定向运动 改变电荷分布, 产生附加场 E’ F qE eE 导体内部电场 感应电场