
第2,3次课程教学方案 周次 4 课时数8 第二章点、直线和平面的投影 章节第三章直线与平面、平面与平面的相对位置 教学了解投影的方法和分类、投影规律:举握点的三面投影规律及两点的相对位置和重影点:掌握三 目标 种投影面平行线和三种投影面垂直线的投影特性,掌握两直线各种相对位置(平行、相交、交叉) 和要 的投影特点:理解三种投影面平行面和三种投影面垂直面的投影特性, 教学正投影法的基本性质,三视图的投影规律:重影点的概念和两点的相对位置:各种位置直线的 重点投影特性:两直线各种相对位置(平行、相交、交叉)的投影特点;各种位置平面的投影特性。 三视图投影规律;两点、两直线的相对位置的判断 难点 主要 ☑课堂讲授 口小组活动 口实验演示 口难点答疑 ☑提问 教学 ☑作业讲评 口实践教学 口考试测验 口其他活动】 使用 ☑文字教材 ☑电子教案 ☑录像材料 口录音材料 口直播课堂 煤体 资源 ☑CAI课件 口IP课件 口其他资源: 作业 或练 配套习题册相关章节
第 2,3 次课程教学方案 周次 3、4 课时数 8 教学 章节 第二章 点、直线和平面的投影 第三章 直线与平面、平面与平面的相对位置 教学 目标 和要 求 了解投影的方法和分类、投影规律;掌握点的三面投影规律及两点的相对位置和重影点;掌握三 种投影面平行线和三种投影面垂直线的投影特性,掌握两直线各种相对位置(平行、相交、交叉) 的投影特点;理解三种投影面平行面和三种投影面垂直面的投影特性。 教学 重点 正投影法的基本性质 ;三视图的投影规律;重影点的概念和两点的相对位置;各种位置直线的 投影特性;两直线各种相对位置(平行、相交、交叉)的投影特点;各种位置平面的投影特性。 教学 难点 三视图投影规律;两点、两直线的相对位置的判断; 主要 教学 方式 课堂讲授 □ 小组活动 □ 实验演示 □ 难点答疑 提问 作业讲评 □ 实践教学 □ 考试测验 □ 其他活动 使用 媒体 资源 文字教材 电子教案 录像材料 □ 录音材料 □ 直播课堂 CAI 课件 □ IP 课件 □ 其他资源: 作业 或练 习 配套习题册相关章节
(空白不够可添加附页) 第二章点、直线和平面的投影 2.1投影方法概述 2.1.1投影法的基本概念 1.投影法 2.投影法的分类 (1)中心投影法 (2)平行投影油 2.1.2正投影法的投影特性 1.实形性 2.积聚性 3.类似性 机械图样采用正投影法绘制, 使所绘图形即反映物体的真实形状和大小,又简单易画。 本教材通常将 投影简称为投影 2.2三视图 物体在一个投影面上的投影不能完全表示其形状,在机械图样中常采用多面投影米表示物体 的形状。 2.2.1三视图的形成 采用互相垂直的三个投影面,建立一个三投影面体系。 把物体放在所建立的三个投影面中间,按正投影的方法,分别向各投影面投射。由前向后投 射,在正面投影面上得到的图形称为主视图,由上向下投射在H面上得到的视图称为俯视图,由 左向右投射在W面上得到的视图称为左视图。 2.2.2三视图的投影规律 板书 三视图的投影规律: 主视图与俯视图共同反映物体的长一称主俯视图长对正: 主视图与左视图共同反映物体的高一称主左视图高平齐: 计 俯视图与左视图共同反映物体的宽一 称俯左视图宽相等。 简言之:长对正、高平齐、宽相等。 2.3点的投影 点是构成物体表面的最基本的几何元素,掌握点的投影规律,是正确绘制三视图的基础。 2.3.1点的投影 1.立体上点的三面投影 2.点的投影规律 点的投影同样遵守长对正、高平齐、宽相等的规律: 点的正面投影和水平投影的连线垂直于X轴。即a'a⊥OX轴,a'a.=aa=x: 点的正面投影和侧面投影的连线垂直于Z轴。即a'a”⊥0Z轴,a'a,=a”a,=Z: 点的水平投影到X轴的距离等于侧面投影到Z轴的距离,即aa,=a”a,=y⅓
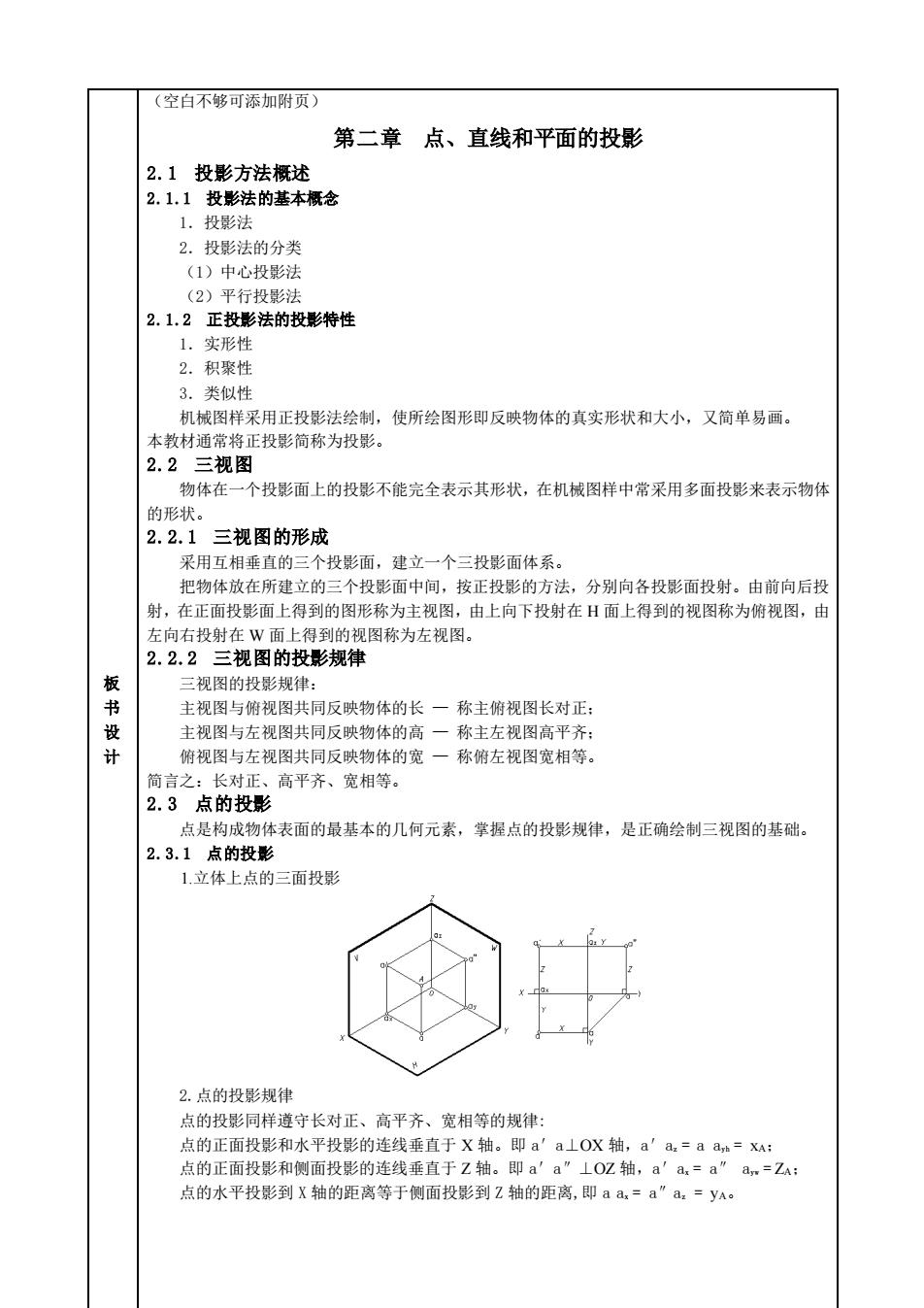
板 书 设 计 (空白不够可添加附页) 第二章 点、直线和平面的投影 2.1 投影方法概述 2.1.1 投影法的基本概念 1.投影法 2.投影法的分类 (1)中心投影法 (2)平行投影法 2.1.2 正投影法的投影特性 1.实形性 2.积聚性 3.类似性 机械图样采用正投影法绘制,使所绘图形即反映物体的真实形状和大小,又简单易画。 本教材通常将正投影简称为投影。 2.2 三视图 物体在一个投影面上的投影不能完全表示其形状,在机械图样中常采用多面投影来表示物体 的形状。 2.2.1 三视图的形成 采用互相垂直的三个投影面,建立一个三投影面体系。 把物体放在所建立的三个投影面中间,按正投影的方法,分别向各投影面投射。由前向后投 射,在正面投影面上得到的图形称为主视图,由上向下投射在 H 面上得到的视图称为俯视图,由 左向右投射在 W 面上得到的视图称为左视图。 2.2.2 三视图的投影规律 三视图的投影规律: 主视图与俯视图共同反映物体的长 — 称主俯视图长对正; 主视图与左视图共同反映物体的高 — 称主左视图高平齐; 俯视图与左视图共同反映物体的宽 — 称俯左视图宽相等。 简言之:长对正、高平齐、宽相等。 2.3 点的投影 点是构成物体表面的最基本的几何元素,掌握点的投影规律,是正确绘制三视图的基础。 2.3.1 点的投影 1.立体上点的三面投影 2.点的投影规律 点的投影同样遵守长对正、高平齐、宽相等的规律: 点的正面投影和水平投影的连线垂直于 X 轴。即 a′a⊥OX 轴,a′az = a ayh = xA; 点的正面投影和侧面投影的连线垂直于 Z 轴。即 a′a″⊥OZ 轴,a′ax = a″ ayw = ZA; 点的水平投影到 X 轴的距离等于侧面投影到 Z 轴的距离,即 a ax = a″az = yA

2.3.2两点的相对位置及重影点 1。两占的相时位置 空间两点的相对位置是指空间两个点的上下、左右、前后关系,也可以由他们的坐标差确定, x坐标值大的在左:y坐标值大的在前:z坐标值大的在上。 2.重影点 当空间两点相对于投影面的在同一条投射线上时,这两点在该投影面上的投影重合,这两点 称为该投影面的面影点。 2.4直线的投影 两点确 “条直线 将两点的同名投影用直线连接,就得到直线的同名投影。 2.4.1各种位置直线的投 在三面投影体系中,直线对投影面的相对位置有一般位置直线、投影面的平行线和投影 面的垂直线三种位置直线,后两种直线统称为特殊位置直线。 1.投影面平行线 平行于一个投影面,而顿斜于另两个投影面的直线,称为投影面的平行线。 正平线、水平线、侧平线。 投影面平行线的投影特性是:投影面的平行线他们所平行的那个投影面上的投影领斜投影轴,反 映直线的实长,直线的另外两面投影平行于相应的投影轴,且投影长度变短。 2.投影面垂直线 垂直于一个投影面,而与另外两个投影面平行的直线称为投影面垂直线: 正垂线、铅垂线、侧垂线 投影面垂直线的投影特性是:直线在所垂直的那个投影面上的投影积聚成为一个点,其他两 投影都反映直线实长,且垂直于相应投影轴。 3。一般位置直线 与三个投影面都处于倾斜位留的直线,称为一般位置直线 一般位置直线的投影特性是:直线的三面投影都与投影轴倾斜:三个投影都小于真长:各个 投影与投影轴的夹角都不反映直线与投影面夹角的真实大小。 2.4.2直线上点的投影 1.从属性若点在直线上,则点的投影必在直线的同名投影上。 2,定比性由于投射线互相平行,直线上的点,分割线段之比等于其投影长度之比。 2.4.3两直线的相对位置 空间两直线的相对位置有:平行、相交、交叉三种情况。 1,平行两直线 如果空间两直线平行,则各组同名投影必定互相平行:反之,如果两直线的同名投影都互相 平行,则直线在空间一定互相平行。 2.相交两直线 如果空间两直线相交,则他们的同名投影也必定相交,而且交点的投影符合空间点的投影规 3.交叉两直线 空间两条既不平行又不相交的直线称为交叉两直线。交叉两直线的各面投影既不符合平行两 直线的投影,又不符合相交两直线的投影规律。 2.5平面的投影 2.5.1平面的表示法 2.5.2各种位置平面的投影 1.投影面的垂直面2.投影面的平行面3.一般位置平面 2.5.3平面内的点和直线 .平面内取直线
2.3.2 两点的相对位置及重影点 1.两点的相对位置 空间两点的相对位置是指空间两个点的上下、左右、前后关系,也可以由他们的坐标差确定。 x 坐标值大的在左;y 坐标值大的在前;z 坐标值大的在上。 2.重影点 当空间两点相对于投影面的在同一条投射线上时,这两点在该投影面上的投影重合,这两点 称为该投影面的重影点。 2.4 直线的投影 两点确定一条直线,将两点的同名投影用直线连接,就得到直线的同名投影。 2.4.1 各种位置直线的投影 在三面投影体系中,直线对投影面的相对位置有一般位置直线、投影面的平行线和投影 面的垂直线三种位置直线,后两种直线统称为特殊位置直线。 1.投影面平行线 平行于一个投影面,而倾斜于另两个投影面的直线,称为投影面的平行线。 正平线、水平线、侧平线。 投影面平行线的投影特性是:投影面的平行线他们所平行的那个投影面上的投影倾斜投影轴,反 映直线的实长,直线的另外两面投影平行于相应的投影轴,且投影长度变短。 2.投影面垂直线 垂直于一个投影面,而与另外两个投影面平行的直线称为投影面垂直线。 正垂线、铅垂线、侧垂线。 投影面垂直线的投影特性是:直线在所垂直的那个投影面上的投影积聚成为一个点,其他两 投影都反映直线实长,且垂直于相应投影轴。 3.一般位置直线 与三个投影面都处于倾斜位置的直线,称为一般位置直线。 一般位置直线的投影特性是:直线的三面投影都与投影轴倾斜;三个投影都小于真长;各个 投影与投影轴的夹角都不反映直线与投影面夹角的真实大小。 2.4.2 直线上点的投影 1.从属性 若点在直线上,则点的投影必在直线的同名投影上。 2.定比性 由于投射线互相平行,直线上的点,分割线段之比等于其投影长度之比。 2.4.3 两直线的相对位置 空间两直线的相对位置有:平行、相交、交叉三种情况。 1.平行两直线 如果空间两直线平行,则各组同名投影必定互相平行;反之,如果两直线的同名投影都互相 平行,则直线在空间一定互相平行。 2.相交两直线 如果空间两直线相交,则他们的同名投影也必定相交,而且交点的投影符合空间点的投影规 律。 3.交叉两直线 空间两条既不平行又不相交的直线称为交叉两直线。交叉两直线的各面投影既不符合平行两 直线的投影,又不符合相交两直线的投影规律。 2.5 平面的投影 2.5.1 平面的表示法 2.5.2 各种位置平面的投影 1.投影面的垂直面 2.投影面的平行面 3.一般位置平面 2.5.3 平面内的点和直线 1.平面内取直线

从立体几何可知,直线在平面上的条件是: (1)若一直线过平面上的两点,则此直线必在该平面内。 (2)若一直线过平面上的一点,且平行于该平面上的另一直线,则此直线也在该平面内, 久2线在平有上名起 平面内取点 点在平面内的直线上,则此点必位于该平面内。所以要在平面上取点,应先在在平面内取直 线作为辅助线,然后再在该直线上取点。 第三章直线与平面、平面与平面的相对位置 3.1平行问题 3.1.1直线与平面平行 几何条件: 若直线平行于平面上任意直线,则线、面平行 上战平 则过平面内任一点必能在平面内作一直线平行于己知直线 3.1.2两平面互相平行 几何条件: 两平面内各有一对相交直线分别对应平行。 3.2相交问题 3.2.1宜线与平面相交 交点的性质: 1.是直线与平面的公有点: 2.是可见与不可见的分界点 3.2.2平面与平面相衣 交线是两平面的公有线。(凡两平面的公有点都在交线上) 2.交线的投影是直线,可由其上两个(公有)点的投影确定 3。求一平面内的一直线与另一平面的交点来确定公有点(转化为线、面交点问题)。 3.3垂直问题 3.3.1直线与特殊位置平面垂直 当直线垂直于特殊位置平面时,平面的积聚性投影垂直于直线的同面投影。 3.3.2两特殊位置平面垂直 两特殊位置平面互相垂直时,它们具有积聚性的同面投影互相垂直
从立体几何可知,直线在平面上的条件是: (1)若一直线过平面上的两点,则此直线必在该平面内。 (2)若一直线过平面上的一点,且平行于该平面上的另一直线,则此直线也在该平面内。 2.平面内取点 从立体几何可知,直线在平面上的条件是: 点在平面内的直线上,则此点必位于该平面内。所以要在平面上取点,应先在在平面内取直 线作为辅助线,然后再在该直线上取点。 第三章 直线与平面、平面与平面的相对位置 3.1 平行问题 3.1.1 直线与平面平行 几何条件: 1. 若直线平行于平面上任意直线,则线、面平行。 2. 若线、面平行,则过平面内任一点必能在平面内作一直线平行于已知直线。 3.1.2 两平面互相平行 几何条件: 两平面内各有一对相交直线分别对应平行。 3.2 相交问题 3.2.1 直线与平面相交 交点的性质: 1. 是直线与平面的公有点; 2. 是可见与不可见的分界点。 3.2.2 平面与平面相交 1. 交线是两平面的公有线。(凡两平面的公有点都在交线上) 2. 交线的投影是直线,可由其上两个(公有)点的投影确定。 3. 求一平面内的一直线与另一平面的交点来确定公有点(转化为线、面交点问题)。 3.3 垂直问题 3.3.1 直线与特殊位置平面垂直 当直线垂直于特殊位置平面时,平面的积聚性投影垂直于直线的同面投影。 3.3.2 两特殊位置平面垂直 两特殊位置平面互相垂直时,它们具有积聚性的同面投影互相垂直

第4次课程教学方案 周次 课时数4 教学 第四章投形变换 章节 学了解几何元素的一般位置和特殊位置分析:理解投影变换的橛念及内容:攀握换面法求直线或平 目标 面对投影面外 般位置时,求其实长、实形、夹角、距离等度量值。 和要 求 教学投形变换的概念及内容:掌握换面法求直线或平面对投影面处于一般位置时,求其实长、实形、 重点夹角、距离等度量值。 用换面法求解一般位置直线、平面的实形,及相对投影面的夹角 难点 主要 ☑课堂讲授 口小组活动 口实验演示 口难点答疑 ☑提问 教学 方式 ☑作业讲评 口实践教学 口考试测验 口其他活动】 使用 ☑文字教材 ☑电子教案 ☑录像材料 口录音材料 口直播课堂 煤体 资源 ☑CAI课件 口IP课件 口其他资源: 作业 配套习题册相关章节 习
第 4 次课程教学方案 周次 5 课时数 4 教学 章节 第四章 投影变换 教学 目标 和要 求 了解几何元素的一般位置和特殊位置分析;理解投影变换的概念及内容;掌握换面法求直线或平 面对投影面处于一般位置时,求其实长、实形、夹角、距离等度量值。 教学 重点 投影变换的概念及内容 ;掌握换面法求直线或平面对投影面处于一般位置时,求其实长、实形、 夹角、距离等度量值。 教学 难点 用换面法求解一般位置直线、平面的实形,及相对投影面的夹角; 主要 教学 方式 课堂讲授 □ 小组活动 □ 实验演示 □ 难点答疑 提问 作业讲评 □ 实践教学 □ 考试测验 □ 其他活动 使用 媒体 资源 文字教材 电子教案 录像材料 □ 录音材料 □ 直播课堂 CAI 课件 □ IP 课件 □ 其他资源: 作业 或练 习 配套习题册相关章节