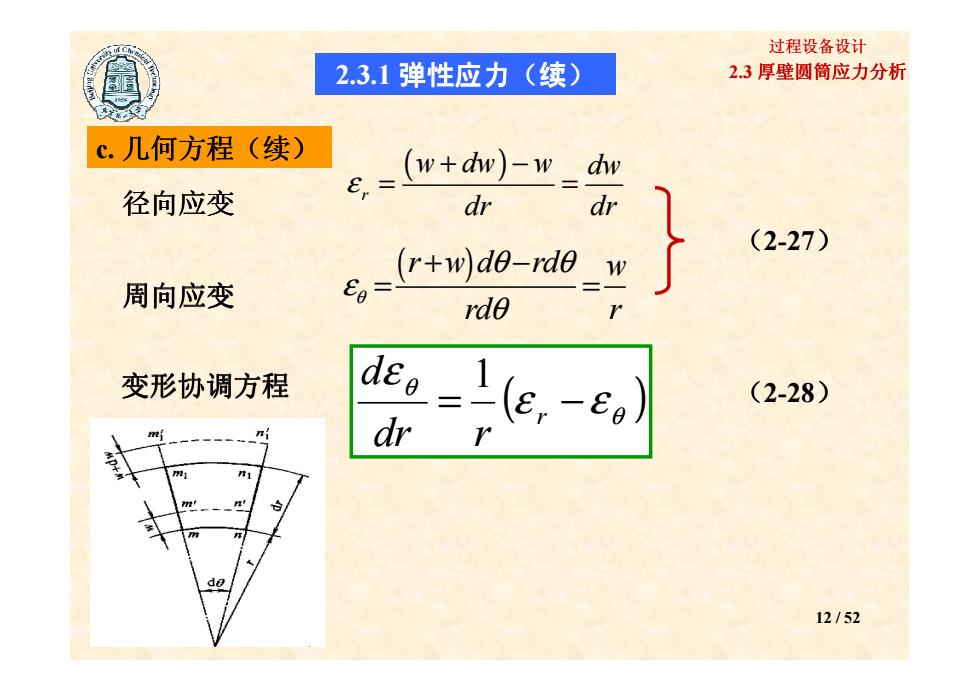
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 c.几何方程(续) (w+dw)-w dw 径向应变 dr dr )do-rdo (2-27) 周向应变 rde 变形协调方程 (2-28) 12/52
2.3 厚壁圆筒应力分析 过程设备设计 c. 几何方程(续) 径向应变 周向应变 ( ) r w dw w dw dr dr ε + − = = (r w d rd ) w rd r θ θ θ ε θ + − = = (2-27) 2.3.1 弹性应力(续) 12 / 52 变形协调方程 ( ) θ θ ε ε ε = r − dr r d 1 (2-28)

过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 d.物理方程 e=言a,-4+a月 (2-29) e,=o。-4a,+a〗 13/52
2.3 厚壁圆筒应力分析 过程设备设计 d. 物理方程 [ ] ( ) [ ( )] r r z E ε = σ − µ σ θ +σ 1 1 (2-29) 2.3.1 弹性应力(续) 13 / 52 [ ( )] r z E ε θ = σ θ − µ σ +σ 1 (2-29)

过程设备设计 2.3.1弹性应力(续)》 2.3厚壁圆筒应力分析 e.平衡、几何和物理方程综合 ◆ 求解应力的微分方程 将式(2-28)中的应变换成应力 =0 并整理得到: dr2 dr 解该微分方程,可得0,的通解。将O,再代入式(2-26) 得09。 B O,=A- B r2 0g=A+ (2-33) 14/52
2.3 厚壁圆筒应力分析 过程设备设计 e. 平衡、几何和物理方程综合 、几何和物理方程综合 求解应力的微分方程 将式(2-28)中的应变换成应力 )中的应变换成应力 并整理得到: 3 0 2 2 + = dr d dr d r σ r σ r 解该微分方程,可得 σ r的通解。将 σ r 再代入式(2-26) 2.3.1 弹性应力(续) 14 / 52 2 r B σ r = A− 2 r B σ θ = A + 解该微分方程,可得 的通解。将 再代入式(2-26) 得 。 σ r σ r σ θ (2-33)
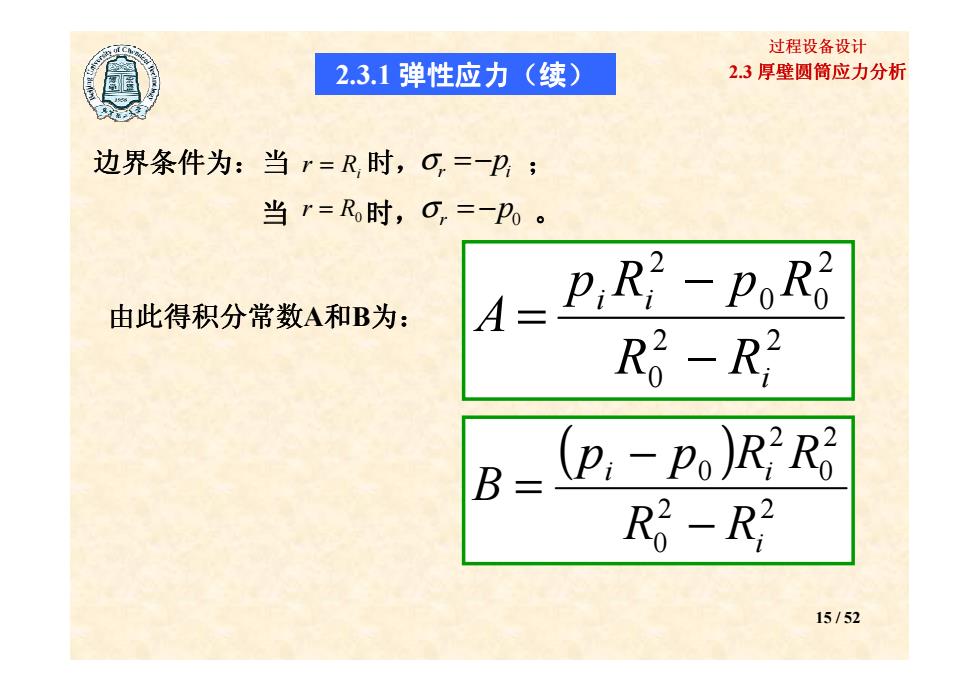
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 边界条件为:当r=R时,O,=一P; 当r=R时,O,=一P0。 PiR2-PoRo 由此得积分常数A和B为: Ro-R2 B (P:-Po)R2Ro Ro-R2 15/52
2.3 厚壁圆筒应力分析 过程设备设计 边界条件为:当 时, ; 当 时, 。 Ri r = σr =−pi R0 r = σr = −p0 由此得积分常数A和B为: 2 2 2 0 0 2 i i R R p R p R A −− = 2.3.1 弹性应力(续) 15 / 52 2 2 R0 − Ri ( ) 2 2 0 2 0 2 0 i i i R R p p R R B − − =
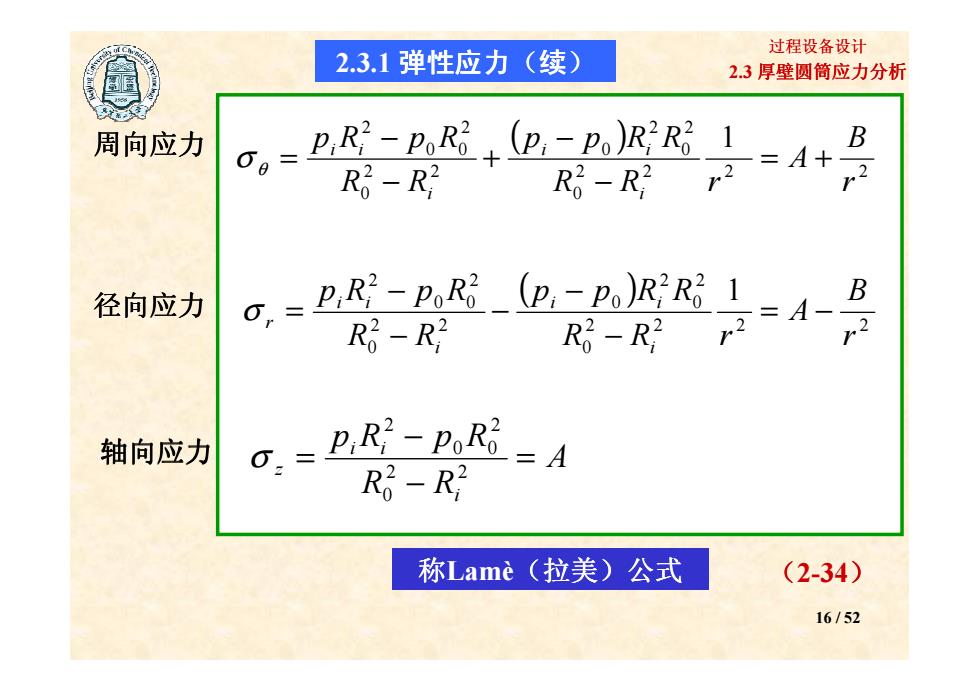
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆简应力分析 周向应力 0o= P.Ri-PoRi (p-Po)R'R:1 B Ro-R2 Ro-R2 + 径向应力 =PRi-Poki_(p.-Po)RRi1 Ro-R2 Ro-R2 轴向应力 P.Ri-PoRi=A Ro-R2 称Lame(拉美)公式 (2-34) 16/52
2.3 厚壁圆筒应力分析 过程设备设计 周向应力 径向应力 ( ) 2 2 2 2 0 2 0 2 0 2 2 0 2 0 0 2 1 r B A R R r p p R R R R p R p R i i i i i i = + − − + −− σ θ = ( ) 2 2 2 2 0 2 0 2 0 2 2 0 2 0 0 2 1 r B A R R r p p R R R R p R p R i i i i i i r = − − − − −− σ = 2.3.1 弹性应力(续) 16 / 52 轴向应力 0 0 R R R R r r − i − i A R R p R p R i i i z = −− = 2 2 0 2 0 0 2 σ 称Lamè(拉美)公式 (2-34)