过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 当仅有内压或外压作用时,拉美公式可以简化,此时,厚壁 圆筒应力值和应力分布分别如表2一1和图2一17: 表21厚壁圆筒的筒壁应力值 受力情况 仅受内压 仅受外压 Po=0 P=0 任意半径r 内壁处 外壁处 任意半径r 内壁处 外壁处 析 处 r=Ri I=Ro 处 r=Ri =R。 -卫K 1 -Pi 0 K2-12 0 -Po e 是 PoK2 2-
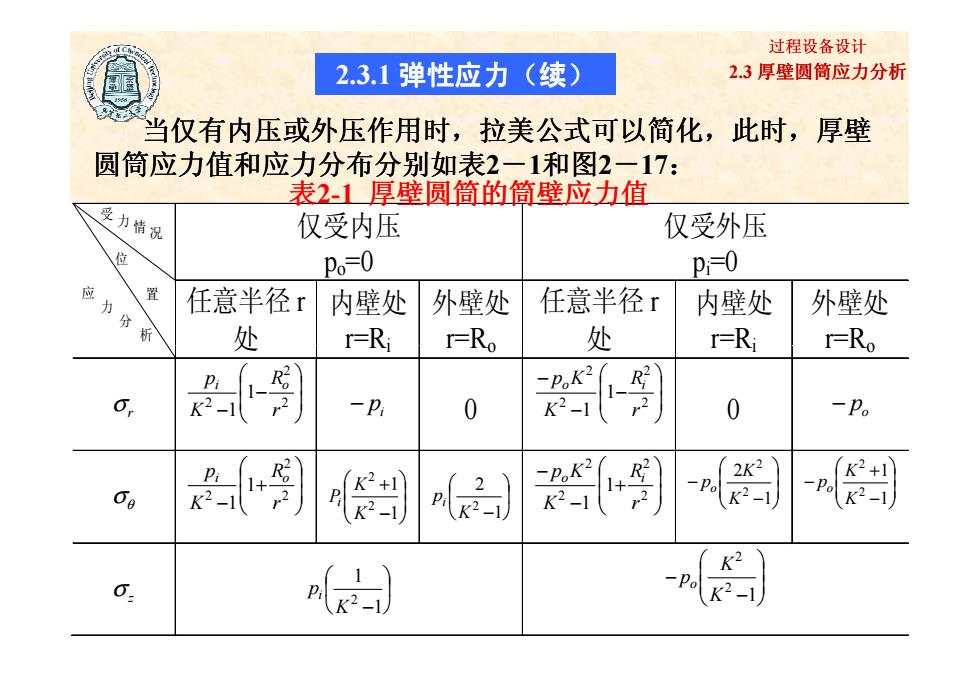
2.3 厚壁圆筒应力分析 过程设备设计 仅受内压 po=0 仅受外压 pi=0 任意半径 r 处 内壁处 r=Ri 外壁处 r=Ro 任意半径 r 处 内壁处 r=Ri 外壁处 r=Ro 受 力 情 况 位 应 置 力 分 析 表2-1 厚壁圆筒的筒壁应力值 当仅有内压或外压作用时,拉美公式可以简化 ,拉美公式可以简化,此时,厚壁 圆筒应力值和应力分布分别如表2-1和图2-17: 2.3.1 弹性应力(续) 17 / 52 处 r=Ri r=Ro 处 r=Ri r=Ro σ r − − 22 2 1 1 rR Kpi o i − p 0 − − − 22 2 2 1 1 rR KpoK i 0 o − p σθ + − 22 2 1 1 rR Kpi o −+11 22 KK Pi −1 22 K pi + − − 22 2 2 1 1 rR KpoK i − − 1 22 2 KK po −+ − 11 22 KK po σ z −1 12 K pi − − 1 2 2 KK po
2.3.1弹性应力(续) 过程设备设计 2.3厚壁圆简应力分析 K2+1 =P K2-1 2 0= Pi ‘emin=p, 2- K2- Ormin =0 K2 0:=-P0 K2-1 Ormax =-Pi Ormax =-Po 6 =-Po K2+1 k2-1 2K2 omax=-Po k2-1 (a)仅受内压 (b)仅受外压 图2-17厚壁圆筒中各应力分量分布
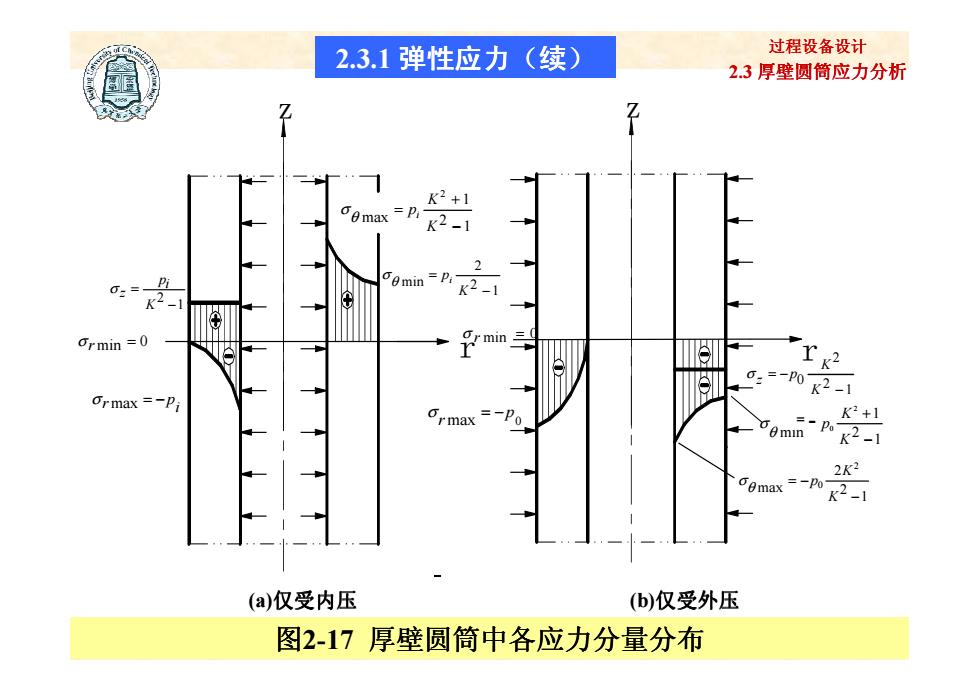
2.3 厚壁圆筒应力分析 过程设备设计 r z r z 1 2 − = K pi σ z min = 0 σ r 1 2 1 max 2 −+ = KK σ θ pi 1 2 2 min − = K p σ θ i min = 0 σ r 2.3.1 弹性应力(续) 2.3 厚壁圆筒应力分析 过程设备设计 18 / 52 r r min = 0 σ r i σ rmax = − p max 0 p r σ = − 1 2 2 0 − = − K K p z σ 1 2 1 min 2 0 −+ = KK p θ σ 1 2 2 max 2 0 − = − K K p θ σ 图2-17 厚壁圆筒中各应力分量分布 (a)仅受内压 (b)仅受外压 =--
过程设备设计 2.3.1弹性应力(续) 2.3厚壁圆筒应力分析 从图2-17中可见, 仅在内压作用下,筒壁中的应力分布规律: ①周向应力O。及轴向应力·:均为拉应力(正值), 径向应力O,为压应力(负值)。 K+1 =P 2-1 2 2 9 x2+1 -x2-1 19/52 (a)仅受内压 (b)仅受外压
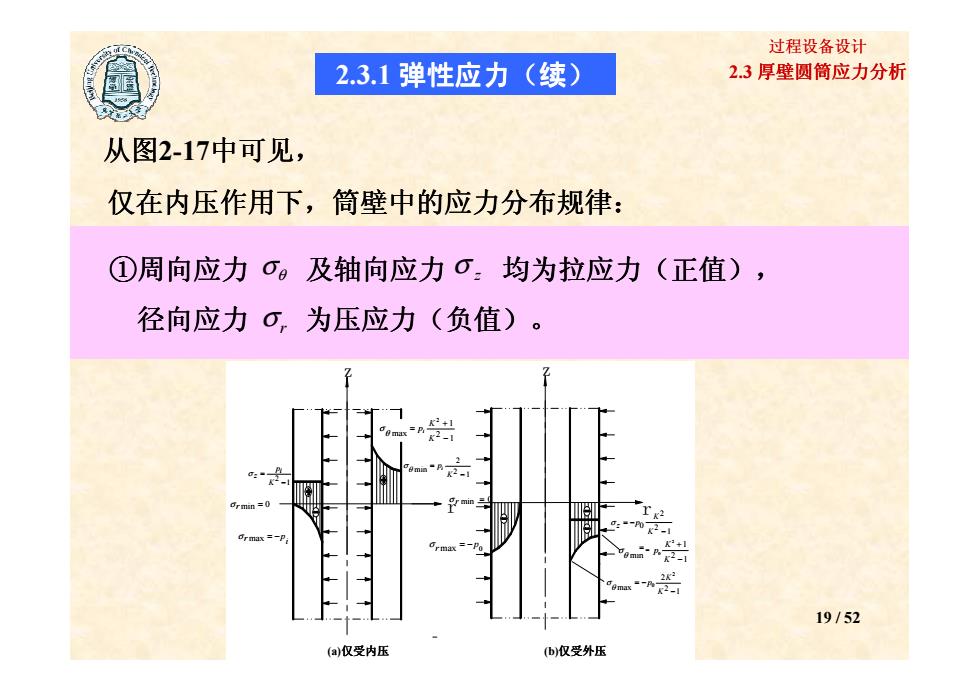
2.3 厚壁圆筒应力分析 过程设备设计 从图2-17中可见, 仅在内压作用下,筒壁中的应力分布规律 ,筒壁中的应力分布规律: ①周向应力 及轴向应力 均为拉应力(正值), 径向应力 为压应力(负值)。 σθ σ z σ r 2.3.1 弹性应力(续) 19 / 52 r z r z 1 2 − = K i p σ z min = 0 σ r i p σ r max = − 1 2 1 max 2 −+ = KK p σ θ i 1 2 2 min − = K p σ θ i σ r min = 0 max 0 p r σ = − 1 2 2 0 − = − K K p z σ 1 2 1 min 2 0 −+ = KK p θ σ 1 2 2 max 2 0 − = − K K p θ σ (a)仅受内压 (b)仅受外压 =-- r z r z 1 2 − = K i p σ z min = 0 σ r i p σ r max = − 1 2 1 max 2 −+ = KK p σ θ i 1 2 2 min − = K p σ θ i σ r min = 0 max 0 p r σ = − 1 2 2 0 − = − K K p z σ 1 2 1 min 2 0 −+ = KK p θ σ 1 2 2 max 2 0 − = − K K p θ σ (a)仅受内压 (b)仅受外压 =--