
computational complexity X[k=G[k+Hk ◆TwoN/2-point DFTs 2(N/2)2 complex multiplications eactly2-l) 2(N/2)2 complex additions xo一 W G[1川 x2I0→ Combining the DFT outputs 2-point WN G[2] x[4]0→ DFT w G[3] 4 N complex multiplications x句o→ w x[1]o→ X[4] 6 ◆N complex additions HIO] x[3]o+ X[5 2-point H1] Total complexity N=8 N=210 DFT H2] 40N2/+N complex multiplicati H 40N2/2+N complex additions. xactly:2+- More efficient than direct DFT when N>2 19
◆Two N/2-point DFTs ◆2(N/2)2 complex multiplications 18 computational complexity ◆Combining the DFT outputs ◆N complex multiplications ◆N complex additions ◆Total complexity ◆N2/2+N complex multiplications ◆N2/2+N complex additions. ◆More efficient than direct DFT when N>2 ◆2(N/2)2 complex additions ( ) 2 exactly: 2 1 2 2 2 N N N − + = N exactly: 2 1 ( ) 2 2 N N − k X k G k W H k N = + N-point DFT computational complexity: ; N=8 40 64 56 40 N=210 32
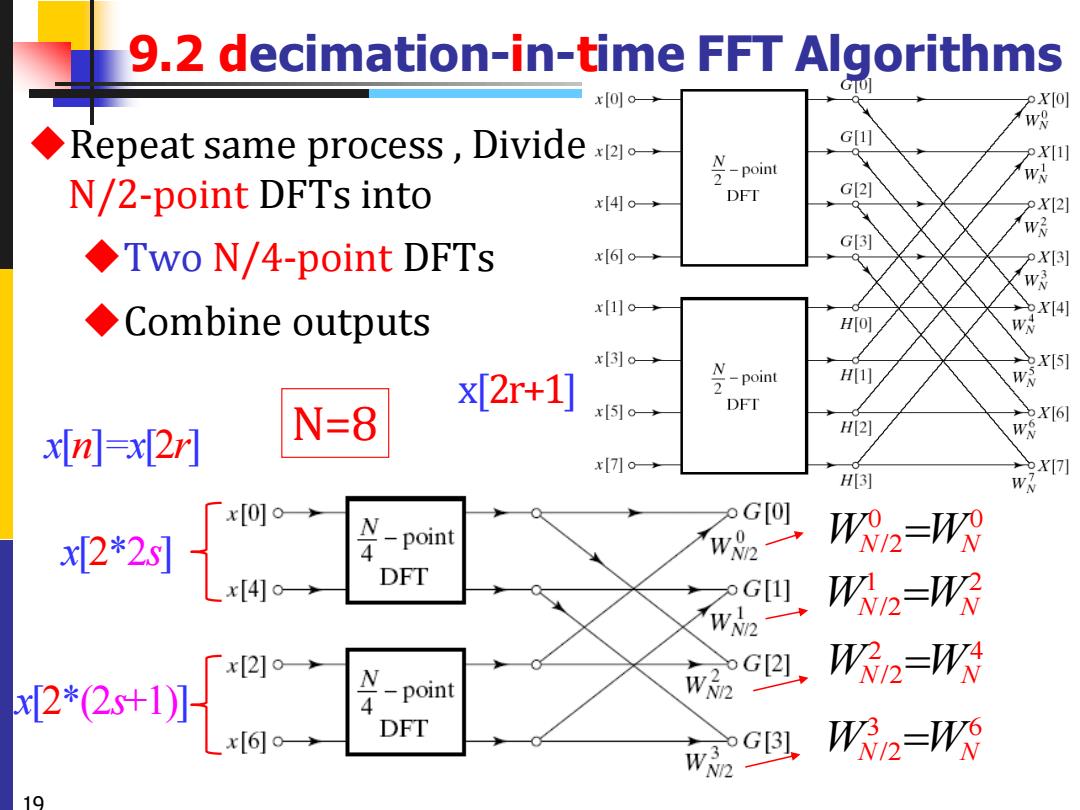
9.2 decimation-in-time FFT Algorithms G0 x00→ X[O] WS ◆Repeat same process,Divide。 G -Point N PX[1] WN N/2-point DFTs into G[2] x[4。→ DFT X[2] w ◆TwoN/4-point DFTs G[3] x[6。→ X[3] w ◆Combine outputs x10→ X[4] H[o] w x3o→ N X5] x[2r+1] 2 -point H DFT N=8 x[5)o→ X6 x[n]=x[2r] H(2] x7]0→ X7列 H(3] x[0]o¥ 2*2列 N G[0] 4 -point w92→ WN2-WS DFT W2=W吹 「x[2] 2*2+1 4 -point w Gel.WR=WN WNR ⑥。→ DFT WNR=WN 10
19 9.2 decimation-in-time FFT Algorithms ◆Repeat same process , Divide N/2-point DFTs into ◆Two N/4-point DFTs ◆Combine outputs N=8 0 0 W W N N /2= 1 2 W W N N /2= 2 4 W W N N /2= 3 6 W W N N /2= x[n]=x[2r] x[2*2s] x[2*(2s+1)] x[2r+1]

9.2 decimation-in-time FFT Algorithms After two steps of decimation in time x[0]o→ X[O] 4-point WR x[40→ DFT →PXT1川 WN x[2]0→ pX[2] 4-point W WR N=8 x[6]o→ DFT X[3] WN N/4=2 x[1]o→ X[4] 4 -point WN DFT x[5]o→ →Xx0]o W x[3]o→ bX0 W四=W吸 N -point w x[7]0→ DFT X[x[4] W-WA2 Repeat until we're left with two-point DFT's 20
20 9.2 decimation-in-time FFT Algorithms ◆After two steps of decimation in time ◆Repeat until we’re left with two-point DFT’s 0 0 W W2 = N 1 /2 2 N W W= N N=8 N/4=2

9.2 decimation-in-time FFT Algorithms flow graph for 8-point decimation in time binary code: x[0] X[O] nnno x[4]o PX[1] WN N=8=23 WR w及 x[2] 3 stages: w时 PX[2] w x[6]o PX[3] N=2m m=log2N x[1叫 X[4] w WN m级:每级乘法 x[5]o →bX[5] 和加法个数为N w x [3]o bX[6] w Computational x[7] X[7] Complexity: WN w WN Nlog2N complex multiplications and additions Nm
21 9.2 decimation-in-time FFT Algorithms ◆flow graph for 8-point decimation in time ◆Computational Complexity: ◆Nlog2N complex multiplications and additions N=2m m=log2N N=8=23 binary code: 2 1 0 n n n 3 stages: m级: 每级乘法 和加法个数为N Nm

9.2 decimation-in-time FFT Algorithms DIT flow graph for 8-point decimation in time x0] XO] N=8=23 we generalized to x[4] X[1] w N=2m x[2] X[2] w m=1og2N x[6]o- W W x 1 X[4] m级:每级乘法 和加法个数为N WOWWB2-WN x[3] 6X[6 Complexity: x S-x17I Nlog2N complex multiplications and Nlog2N additions Nm Nm D?
22 9.2 decimation-in-time FFT Algorithms ◆DIT flow graph for 8-point decimation in time ◆Complexity: Nlog2N complex multiplications and Nlog2N additions 2 WN 0 WN 4 WN 6 WN N=2m m=log2N N=8=23 3 WN 7 WN generalized to m级: 每级乘法 和加法个数为N 3 /2 N =W WN N 2 /2 N W WN N = 0 WN 0 4 / 2= N N W W NWN Nm Nm