
Second Order Goertzel Filter 除n=0时y[0]=xf0],ym对每 实现极点因式 个n有2个实数乘,4个实数加 -+2cos0.1. 实现零点因式: ylN]yN]WyN-1]=Xk,k=0,1,...,N-1 same Complexity for one x[k](x[n],y[n]is complex). yAnl=-yAn-2+2cos2z(N-Kyin-I+xfn.n-0.1N total:2(N+2)real X and 4(N+1)real + 乘N 12 Complexity for all N X[k] 近似 Each pole is used for X[k],X[N-k],k=0.1.... Approximately N2 real multiplications and 2N2 real additions.More efficient than the direct method. 4N2 real X N(4N-2)real
12 Second Order Goertzel Filter ◆Complexity for one X[k] ( x[n], y[n] is complex). ◆Poles: 2N real multiplications and 4N real additions ◆Zeros: computed only once: 4 real ×and 4 real + . 2 y n y n y n x n [ ] [ 2] 2cos [ 1] [ ], 0,1,..., N n N k =− − + − + = [ ] [ ] [ 1] N k y y W k N = − − N Ny =Xk, k=0,1,..., -1 N total: 2(N+2) real ×and 4(N+1) real + . ◆Complexity for all N X[k] ◆Each pole is used for X[k], X[N-k] ◆Approximately N2 real multiplications and 2N2 real additions. 2 ( ) y n y n y n x n [ ] [ 2] 2cos [ 1] [ ], 0,1,..., N N k n N − =− − + − + = same ◆More efficient than the direct method. 除n=0时y[0]=x[0], y[n]对每 个n有2个实数乘, 4个实数加 乘 N , 0,1,..., -1 2 N k = 实现极点因式: 实现零点因式: /2 4N2 real × N(4N-2) real + Complexity of first Order Goertzel Filter for one X[k]: all 近似

9.2 Decimation-in-Time FFT Algorithms Makes use of periodicity and symmetry ofW Consider special case of N=2v:integer v power of 2 Separatexn]into two sequences of length N/2 Even-numbered sequence N:Length of x[n] Odd-numbered sequences. N-point DFT X[k-∑nke/NKn ejexlN)=W n=( =∑n]W+∑]W收 n even n odd 14
14 9.2 Decimation-in-Time FFT Algorithms ◆Makes use of periodicity and symmetry of ◆Consider special case of N=2ν : integer ν power of 2 ◆Separate x[n] into two sequences of length N/2 ◆Even-numbered sequence ; ◆Odd-numbered sequences . ( ) 1 0 2 / [ ] , N n j kn N X k x n e − = − = n even [ ] kn = + x nWN =WN j(2 /N) e − kn WN n odd [ ] kn x nWN N: Length of x[n] N-point DFT

9.2 decimation-in-time FFT Algorithms X[-芝=∑n+∑ n=0 n even n odd Substitute variables n=2r for n even and n=2r+1 for odd N/2 X[F∑, 2r]+∑2r+H7 WW吹 N/2-point DFT 二 灯2r]W+W 灯2r+1]W2 N/21 G[]=∑gr]W g(r] r=0 hr] r=0 =-Gk猴H[=e及2-eā=mn N/2-1 H[∑h r=( G[k]and H[k]are the N/2-point DFTs ofeach subsequence: g[n]=x[2n]and h(n]=x2n1].0
15 9.2 decimation-in-time FFT Algorithms 2 (2 1) /2 1 /2 1 r 0 r 0 [ ] [ ] 2 2 1 N k N r r N N k X k x W x W r r − − = = + = + + ◆Substitute variables n=2r for n even and n=2r+1 for odd ◆G[k] and H[k] are the N/2-pointDFTs of each subsequence: g[n]=x[2n] and h[n]=x[2n+1] n even n odd 1 0 [ ] [ ] [ ] N N kn kn N kn n X k x nW x nW x nWN − = = = + , k = + G k H k WN 1 1 r 0 r /2 / 0 / / 2 2 2 [ ] ] 2 1 [2 rk k rk N N N N N x W W x W r r − − = = = + + 2 / 2 2 /2 2 2 N N N j j W W e e N − − = = = , 0,1,..., -1 2 N n= 1 0 /2 /2 r [ ] N r N k G g k r W − = = N/2-pointDFT g[r] h[r] 2r N k k W WN , 0,1,.. - . ., 1 2 N k= 1 0 /2 /2 r [ ] N r N k H h k r W − = = N=2r

9.2 decimation-in-time FFT Algorithms r=0 -G(》]+[]。 k-N ,N-1 >k=0,1.,N-1 Xk+ck++]=G网+H个 Nm-eǎnN四-e杨-袋 G+今G内,4+于个 G[k]and H[k]are the N/2-point DFTs ofeach subsequence: g[n]=x[2n]andh[n]=x[2n+1] n=01,-1,k=01
16 9.2 decimation-in-time FFT Algorithms N , k = + G W k H k /2 /2 / 2 1 1 r 0 r 0 / 2 [2 ] [2 1] N rk N N N k kr X x r W W W k N x r − − = = = + + / 2 2 ( ) / 2 /2 ( /2) r N k N j r k N N W e + − + = , 2 G k N G k = + 2 k k N H H = + 0,1,..., 1 2 N k= − ,..., -1 2 N k N = 2 2 2 2 k N N X k G k W H N N k + N + + + = + 2 k N N G k W H k + = + (( )) (( )) 2 2 , k G k H k N N WN = + /2 2 /2 N rk j rk e N W − = = ◆G[k] and H[k] are the N/2-pointDFTs of each subsequence: g[n]=x[2n] and h[n]=x[2n+1] k N =0,1,..., -1 g[r] h[r] , 0,1,..., -1 2 N n= , 0,1,.. - . ., 1 2 N k = , k =0,1,...,N-1
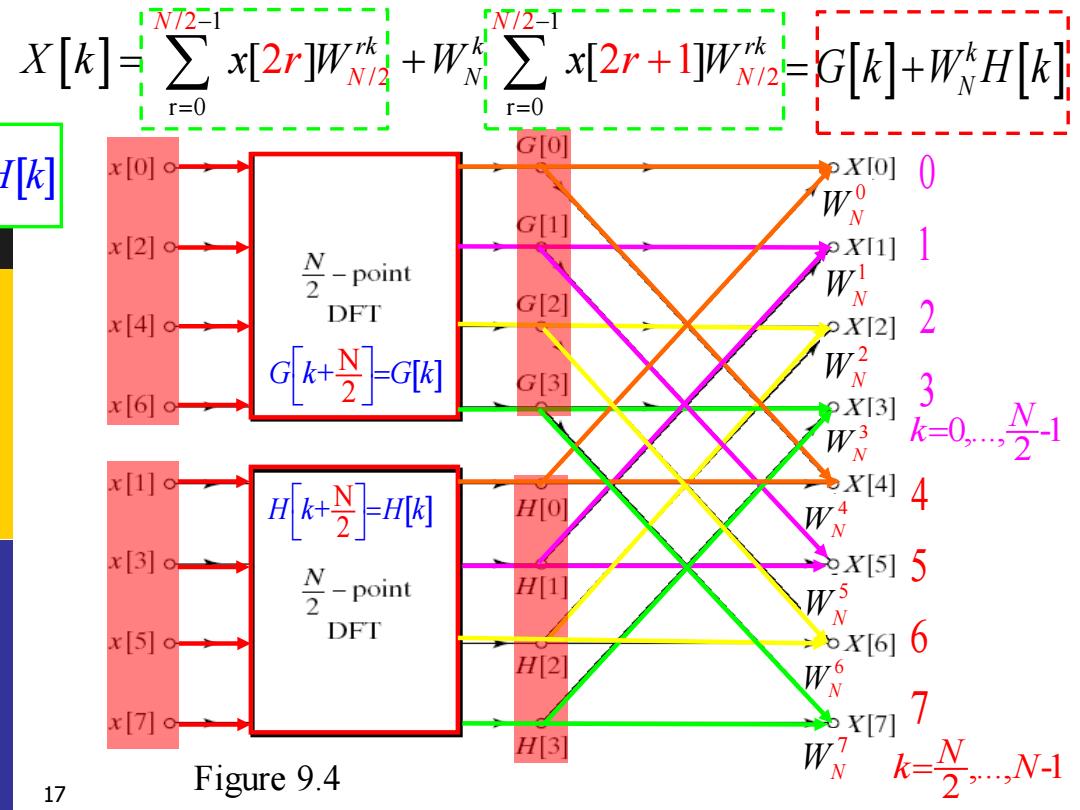
1N7221 N/2-I X[个之2r]w+w∑2r+G[+WH[k I r=0 r=0 GIo] L 咽 0 x[2]o 1 x[4]o DFT 2 x[61o Gk+o啊 明 X3] 3 0 x[1]o k+斗 X[4] 4 x[3]o, N -point x[55 2 x[5]o DFT bX[6] 6 x[7]o [7] 7 17 Figure 9.4 N-
8-point DFT using DIT 17 Figure 9.4 /2 /2 /2 /2 1 1 r 0 r 0 [ ] 2 2[ ]1 N rk N N k r N k X k x W WN r x r W − − = = = + + k G k W H k N = + 0 1 2 3 4 5 6 7 2 2 k N N X k G k W H k N + + = + N 2 G k G k + = N 2 H k H k + = 0 WN 1 WN 2 WN 3 WN 4 WN 5 WN 6 WN 7 WN ,..., -1 2 N k N = 0,..., -1 2 N k=