
§5灵敏度分析 在线性规划问题中,目标函数、约束条件的系数以及资 源的限制量等都当作确定的常数,并在这些系数值的基础 求得最优解。但是实际上,这些系数或资源限制量并非一成 不变的,它们是一些估计或预测的数字,比如价值系数随着 市场的变化而变化,约束系数随着工艺的变化或消耗定额的 变化而变化,计划期的资源限制量也是经常变化的。当这些 系数发生变化时,最优解会受到什么影响?最优解对哪些参 数的变动最敏感?搞清这些问题会使我们在处理实际问题时 具有更大的主动性和可靠性。 分析线性规划模型的某些系数或限制数的变动对最优解。 的影响,被称作灵敏度分析。 灵敏度分析主要解决两个问题: (I)这些系数在什么范围内变化时,原先求出的最优解或 最优基不变?即最优解相对参数变化的稳定性。 (2)如果系数的变化引起了最优解的变化,如何用最简便 的方法求出新的最优解
§5 灵敏度分析 在线性规划问题中,目标函数、约束条件的系数以及资 源的限制量等都当作确定的常数,并在这些系数值的基础上 求得最优解。但是实际上,这些系数或资源限制量并非一成 不变的,它们是一些估计或预测的数字,比如价值系数随着 市场的变化而变化,约束系数随着工艺的变化或消耗定额的 变化而变化,计划期的资源限制量也是经常变化的。当这些 系数发生变化时,最优解会受到什么影响?最优解对哪些参 数的变动最敏感?搞清这些问题会使我们在处理实际问题时, 具有更大的主动性和可靠性。 分析线性规划模型的某些系数或限制数的变动对最优解 的影响,被称作灵敏度分析。 灵敏度分析主要解决两个问题: ⑴这些系数在什么范围内变化时,原先求出的最优解或 最优基不变?即最优解相对参数变化的稳定性。 ⑵如果系数的变化引起了最优解的变化,如何用最简便 的方法求出新的最优解

下面分别介绍各类参数变化的灵敏度分析。 5.1目标函数中价值系数C的分析 分别就非基变量和基变量的价值系数两种情况来讨论: 1.设非基变量x的价值系数c,有增量△c其它参数不 变,求△c的范围使原最优解不变。 由于℃是非基变量的价值系数,因此它的改变仅仅影响 检验数σ的变化,而对其它检验数没有影响。 由o=C;+△C;-CgBP,=o+△c≤0 知,当△C≤-o时,原最优解不变。 2.设基变量Xr的价值系数CBr有增量△Cr,其它参数 变,求△C的范围使原最优解不变。 由于C是基变量的价值系数,因此它的变化将影响所 有非基变量检验数的变化。 由新的非基变量检验数:可=C,C。+0AC0p-, -0(0.△Cr0)B-1P0aj△Cgr≤0,可知,当 max{c,/arj arj>0}≤△Cr≤min{o,/ari arj<0}时,原 最优解不变
下面分别介绍各类参数变化的灵敏度分析。 5.1 目标函数中价值系数C的分析 分别就非基变量和基变量的价值系数两种情况来讨论: ⒈设非基变量xj的价值系数cj,有增量△cj,其它参数不 变,求△cj的范围使原最优解不变。 由于cj是非基变量的价值系数,因此它的改变仅仅影响 检验数σj的变化,而对其它检验数没有影响。 由 σj+△cj≤0 知,当△cj≤-σj 时,原最优解不变。 ⒉设基变量XBr的价值系数CBr有增量△CBr,其它参数不 变,求△CBr的范围使原最优解不变。 由于CBr是基变量的价值系数,因此它的变化将影响所 有非基变量检验数的变化。 由新的非基变量检验数: =σj-(0…△CBr…0)B -1Pj =σj-arj△CBr≤0,可知,当 max{σj /arj│arj>0}≤△CBr≤min{σj /arj│arj<0}时,原 最优解不变。 j j j σ c - C ΔC B P 1 B Br − = + 0 0 = + − = j 1 j j j B σ c Δc -C B P
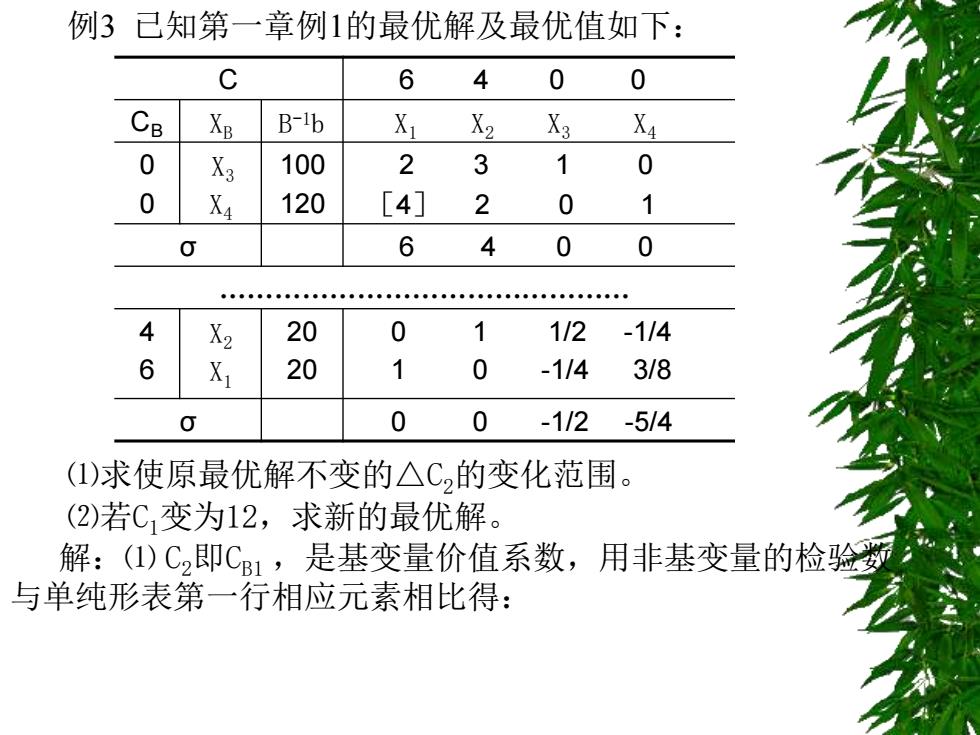
例3 已知第一章例1的最优解及最优值如下: C 6 4 0 0 CB X B-16 X1 X2 X3 X4 0 X3 100 2 3 1 0 0 X4 120 [4] 2 0 1 0 6 4 0 0 4 X2 20 112 -1/4 6 X 20 0 -1/4 3/8 O 0 0 -112 -5/4 (1)求使原最优解不变的△C,的变化范围。 (2)若C1变为12,求新的最优解。 解:(I)C即C1,是基变量价值系数,用非基变量的检验数 与单纯形表第一行相应元素相比得:
例3 已知第一章例1的最优解及最优值如下: C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 0 0 X3 X4 100 120 2 3 1 0 [4] 2 0 1 σ 6 4 0 0 ……………………………………… 4 6 X2 X1 20 20 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4 ⑴求使原最优解不变的△C2的变化范围。 ⑵若C1变为12,求新的最优解。 解:⑴ C2即CB1 ,是基变量价值系数,用非基变量的检验数 与单纯形表第一行相应元素相比得:
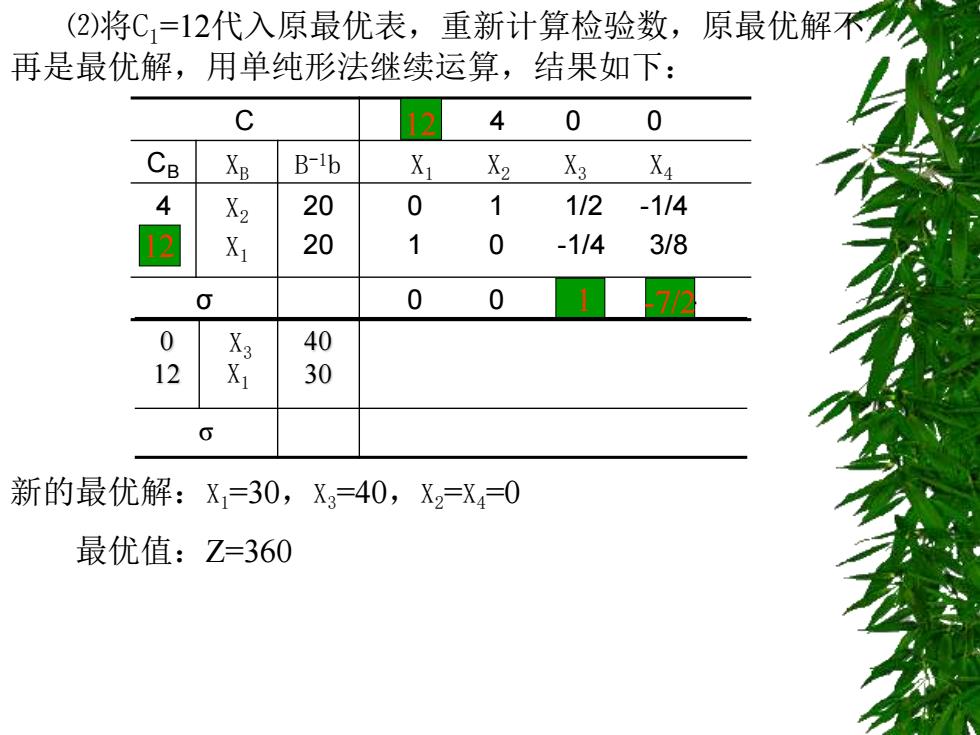
(2)将C,=12代入原最优表,重新计算检验数,原最优解不 再是最优解,用单纯形法继续运算,结果如下: C 4 0 0 CB X B-ib X X2 X3 X4 4 X2 20 0 1 1/2 -1/4 12 X 20 1 0 -1/4 3/8 0 0 0 0 X3 40 12 X 30 新的最优解:X1=30,X3=40,X2=X4=0 最优值:Z=360
⑵将C1=12代入原最优表,重新计算检验数,原最优解不 再是最优解,用单纯形法继续运算,结果如下: C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 4 6 X2 X1 20 20 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4 12 12 1 -7/2 0 12 X3 X1 40 30 σ 新的最优解:X1=30,X3=40,X2 =X4=0 最优值:Z=360

5.2资源系数b的分析 设b:有增量△b,其它参数不变,则b:的变化将影响基变 量所取的值,但对检验数没有影响,记新的基变量为X。,则 又=B-b+0,ab0=Bb+Bab 这里BB是原最优基逆阵B的第列。如果变化后仍存 X≥0,则原最优基不变。由此可知,当△b满足 B 时,原最优基不变。 结果说明,△b:的变化范围是由原基变量的相反数与B1的 第列元素的比值所确定的。 如果△b:不在上述范围变动,则变化后的基变量所取值 区,肯定会出现负分量,但由于△b:不影响检验数的变化,因 此可以用X取代原最优解XBb,以该解为初始解,用对偶 单纯形法继续求解
5.2 资源系数b的分析 设bi有增量△bi,其它参数不变,则bi的变化将影响基变 量所取的值,但对检验数没有影响,记新的基变量为 ,则 这里 是原最优基逆阵B-1的第i列。如果变化后仍有 ≥0,则原最优基不变。由此可知,当△bi满足 ≤△bi≤ 时,原最优基不变。 结果说明 ,△bi的变化范围是由原基变量的相反数与B-1的 第i列元素的比值所确定的。 如果△bi不在上述范围变动,则变化后的基变量所取值 肯定会出现负分量,但由于△bi不影响检验数的变化,因 此可以用 取代原最优解XB =B -1b ,以该解为初始解,用对偶 单纯形法继续求解。 i -1 mi -1 1i -1 i 1 XB B b 0, ,Δb , ,0 B b B B •Δb − = + = + T T ,, B X T -1 mi -1 1i B ,,B B X − − − − B 0 B B b max 1 1 ki ki k 1 k − − − − B 0 B B b min 1 1 ki ki k 1 k B X B X