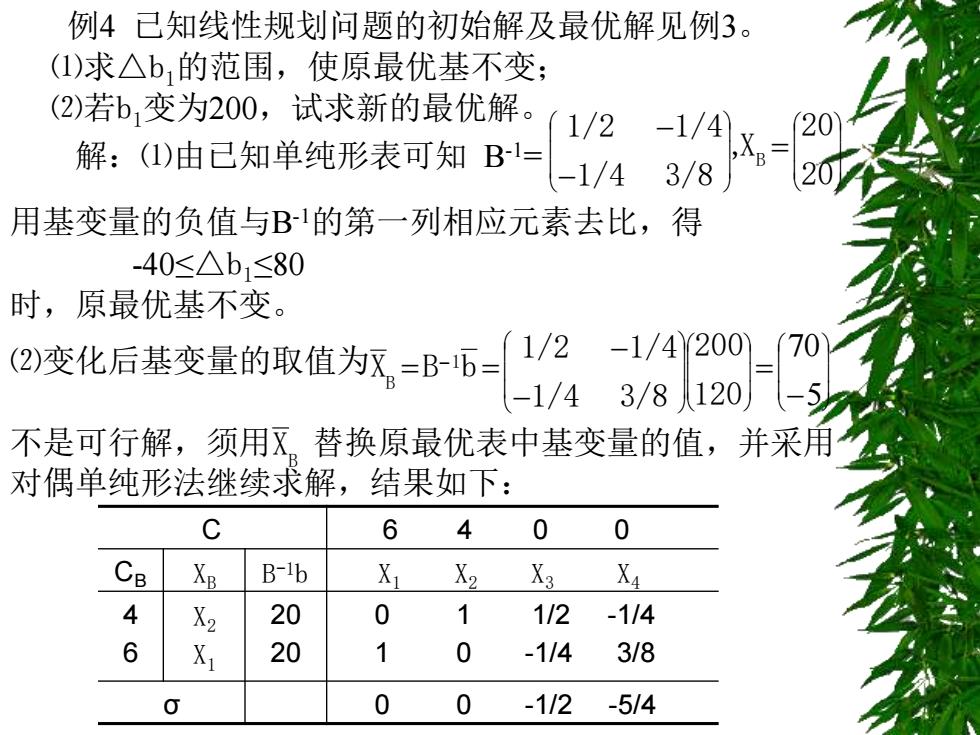
例4已知线性规划问题的初始解及最优解见例3。 (1)求△b,的范围,使原最优基不变; (2)若b,变为200,试求新的最优解。 (1/2 20 解:(I)由己知单纯形表可知B1= -1/4 3/8 20 用基变量的负值与B的第一列相应元素去比,得 40≤△b1≤80 时,原最优基不变。 (2)变化后基变量的取值为X=B-6= 1/2-1/4200)(70 -1/4 3/8120 -5 不是可行解,须用区替换原最优表中基变量的值,并采用 对偶单纯形法继续求解,结果如下: C 6 4 0 0 CB XB B-ib X X2 X3 X4 4 X2 20 0 1 1/2-114 6 X1 20 1 0 -114 3/8 g 0 0 -112 -5/4
例4 已知线性规划问题的初始解及最优解见例3。 ⑴求△b1的范围,使原最优基不变; ⑵若b1变为200,试求新的最优解。 解:⑴由已知单纯形表可知 B-1= = − − 20 20 ,X 1/4 3/8 1/2 1/4 B 用基变量的负值与B-1的第一列相应元素去比,得 -40≤△b1≤80 时,原最优基不变。 ⑵变化后基变量的取值为 − − = − − = = 5 70 120 200 1/4 3/8 1/2 1/4 X B b 1 B 不是可行解,须用 替换原最优表中基变量的值,并采用 对偶单纯形法继续求解,结果如下: B X C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 4 6 X2 X1 20 20 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4
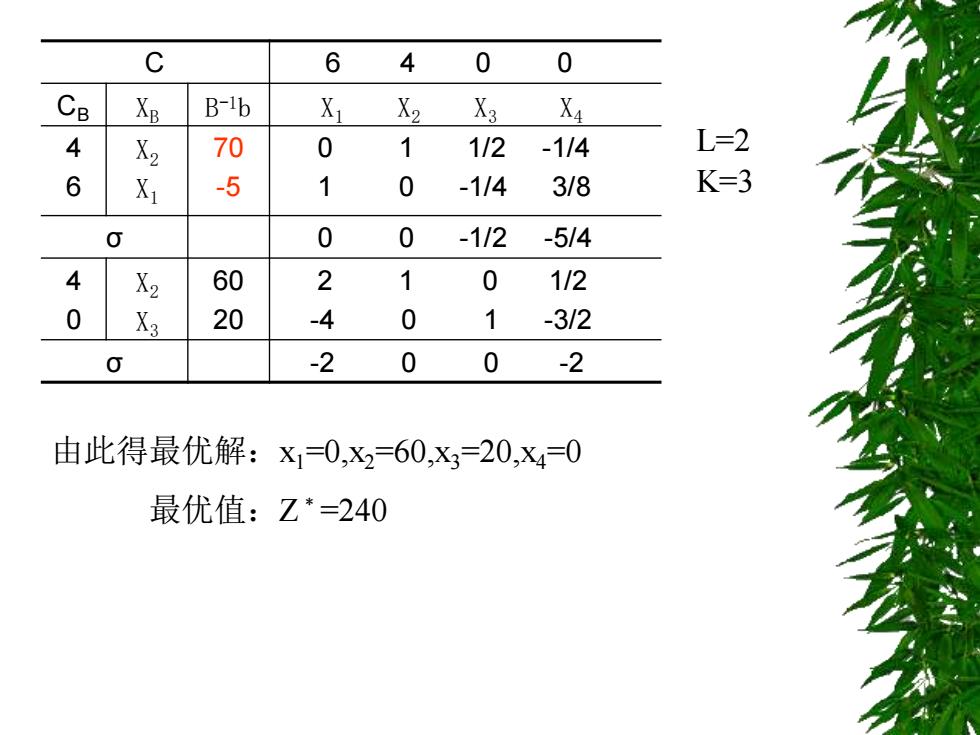
C 6 4 0 0 CB Xs B-ib X X2 X3 X4 4 X2 70 0 1 1/2-1/4 L=2 6 X1 -5 1 0 -1/4 3/8 K=3 O 0 0 -1/2 -5/4 4 X2 60 2 1 0 1/2 0 20 -4 0 -3/2 O -2 0 0 -2 由此得最优解:X1=0,x2=60,x3=20,x40 最优值:Z*=240
C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 4 6 X2 X1 70 -5 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4 4 0 X2 X3 60 20 2 1 0 1/2 -4 0 1 -3/2 σ -2 0 0 -2 L=2 K=3 由此得最优解:x1=0,x2=60,x3=20,x4=0 最优值:Z﹡=240

5.3系数矩阵A的分析 以下分4种情况讨论系数矩阵的变化。 1.增加一个新变量的分析 设X+1是新增加的变量,其对应的系数列向量为Pn+1, 值系数为C1,试讨论原最优解有无改变?及如何尽快地求 出新的最优解。 如果原问题增加一个新变量,则系数矩阵增加一个列; 注意到新增加的列在以B为基的单纯形表中应变为BPn+1, 所以可先计算BP1及o+=Cn+1CB-Pn1,若oH10,则原最 优解不变,反之可将BP+1增填到原最优表的后面,用单纯 形法继续迭代。 例5设第一章例1的原线性规划问题中考虑生产Ⅲ型计 算机,已知生产每台Ⅲ型计算机所需原料4个单位,工时3 个单位,可获利润8个单位。试问该厂是否应该生产Ⅱ型 计算机?如果生产,应该生产多少?
5.3 系数矩阵A的分析 以下分4 种情况讨论系数矩阵的变化。 1.增加一个新变量的分析 设xn+1是新增加的变量,其对应的系数列向量为Pn+1,价 值系数为Cn+1,试讨论原最优解有无改变?及如何尽快地求 出新的最优解。 如果原问题增加一个新变量,则系数矩阵增加一个列, 注意到新增加的列在以B为基的单纯形表中应变为B -1Pn+1 , 所以可先计算B -1Pn+1及σn+1 =Cn+1-CBB -1Pn+1,若σn+1≤0,则原最 优解不变,反之可将B -1Pn+1增填到原最优表的后面,用单纯 形法继续迭代。 例5 设第一章例1的原线性规划问题中考虑生产Ⅲ型计 算机,已知生产每台Ⅲ型计算机所需原料4个单位,工时3 个单位,可获利润8个单位。试问该厂是否 应该生产 Ⅲ型 计算机?如果生产,应该生产多少?