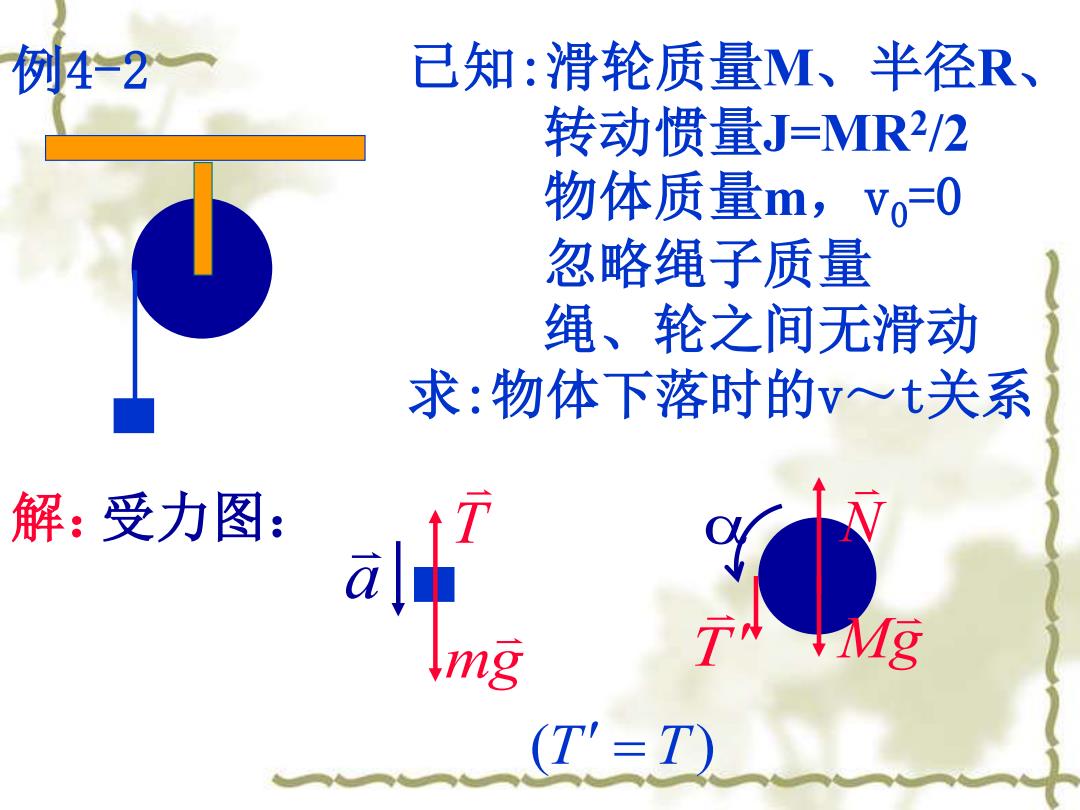
例4-2一 已知:滑轮质量M、半径R、 转动惯量J=MR2/2 物体质量m,v0=0 忽略绳子质量 绳、轮之间无滑动 求:物体下落时的v~t关系 解:受力图: Img (T'=T)
例4-2 已知:滑轮质量M、半径R、 转动惯量J=MR2 /2 物体质量m,v0=0 忽略绳子质量 绳、轮之间无滑动 求:物体下落时的v~t关系 解:受力图: T a mg (T = T) T Mg N

对物体:ng-T=ma ① 对滑轮:TR=MR2·&=MRa ② ①②→a=2mg/(2m+M) .·a=const. v=at =2mgt/(2m+M) Note: 绳中张力T<mg
对物体: mg −T = ma ① 对滑轮: TR MR 1 2 MRa ② 2 2 1 = = ①②→ a = 2mg /(2m + M ) a = const. v = at = 2mgt /(2m+ M) Note: 绳中张力 T mg

例4-3己知:圆盘转动惯量J,初角速度o 阻力矩M=-kO(k为正的常量) 求:o从Q,变为0/2所需的时间 解:转动定律:-ko=Jdo/dt 00 do 2 0 JIn 2 >1 k [思考]o从任意值变为其一半值所需的时间?
例4-3 已知: 圆盘转动惯量J,初角速度0 阻力矩M=-k (k为正的常量) 求: 从0变为0/2所需的时间 解:转动定律: -k=Jd/dt → − = 2 0 0 0 d dt J t k k J t ln 2 → = [思考]从任意值变为其一半值所需的时间?
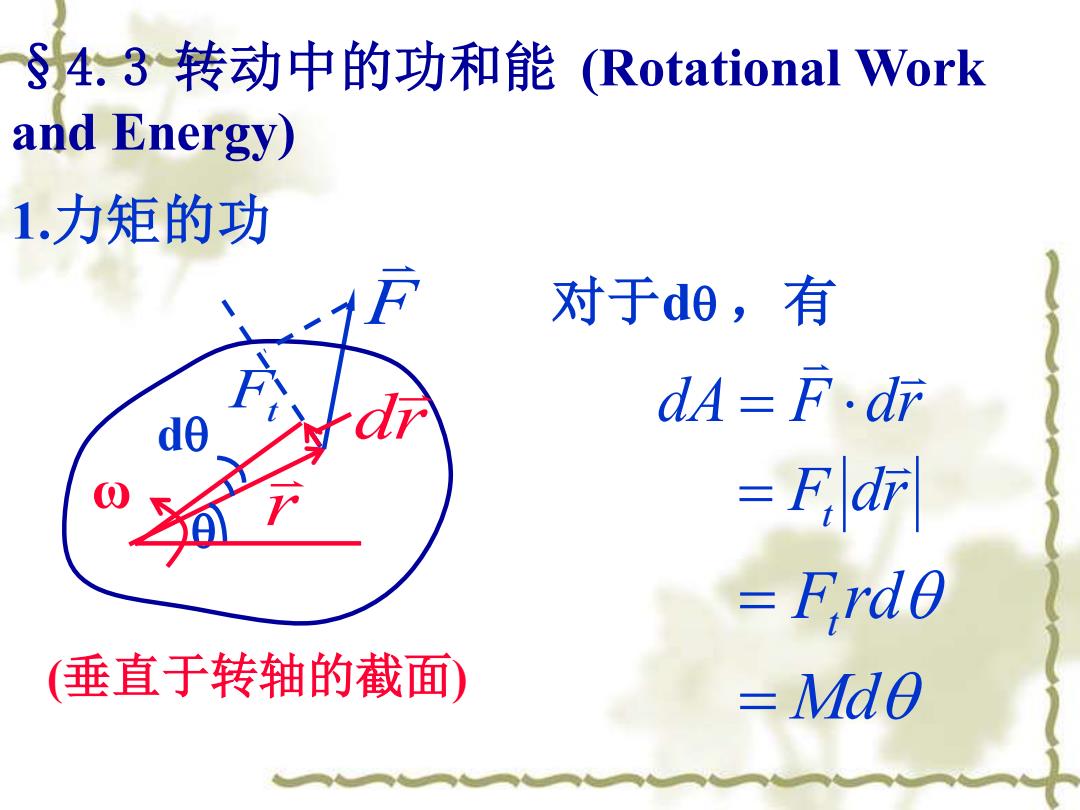
S4.3转动中的功和能(Rotational Work and Energy) 1.力矩的功 对于d旧,有 dA=F.dr =Fdr =F,rde (垂直于转轴的截面) Md0
§4.3 转动中的功和能 (Rotational Work and Energy) 1.力矩的功 对于d ,有 dA F dr = = Md = Ft rd F dr t = (垂直于转轴的截面) d ω r dr F Ft