S4.2定轴转动定律(The Law of Rotation About a Fixed Axis) M=Ja 合外 转动 角加 力矩 惯量 速度 Notes: ①M=∑M=∑F4r=∑Frr;sin M,可正可负
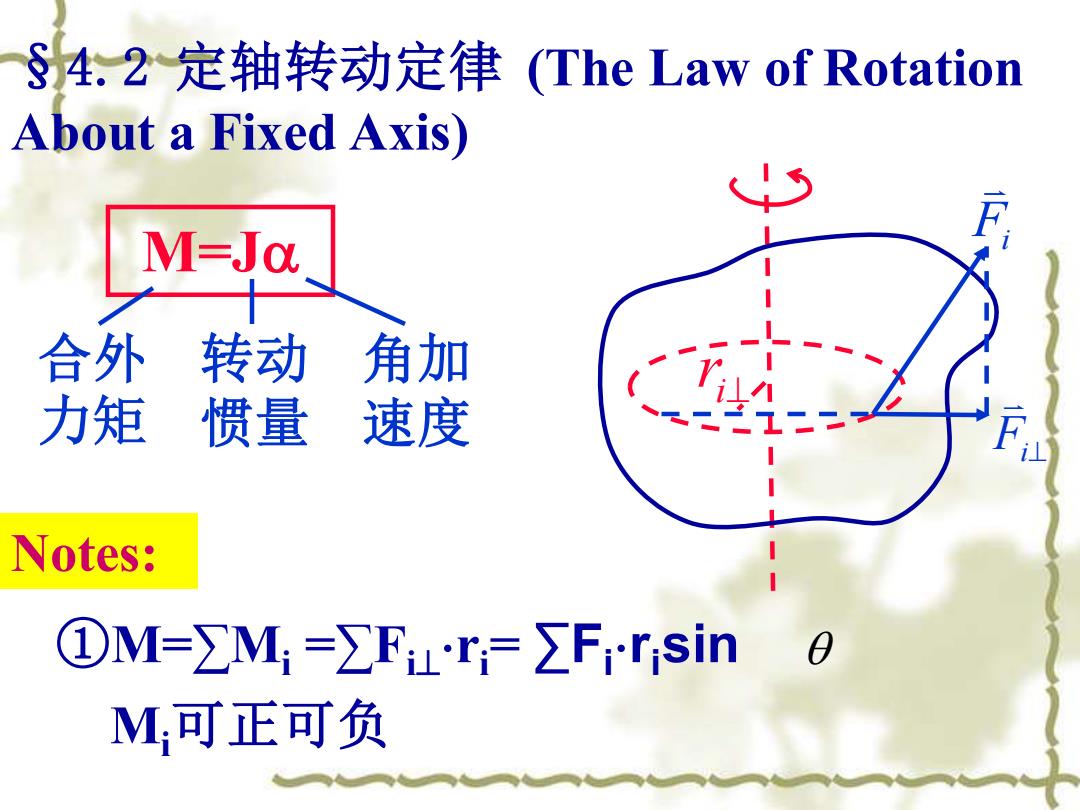
§4.2 定轴转动定律 (The Law of Rotation About a Fixed Axis) M=J ①M=∑Mi =∑Fi⊥ ri= ∑Fi risin 合外 力矩 转动 惯量 角加 速度 Notes: i⊥ r Fi Fi⊥ Mi可正可负
②刚体的重力矩等于刚体全部质量集中于 质心时所产生的重力矩 e.g.细杆质量m,长L 50 mg 重力短:M=mg2 cos 0
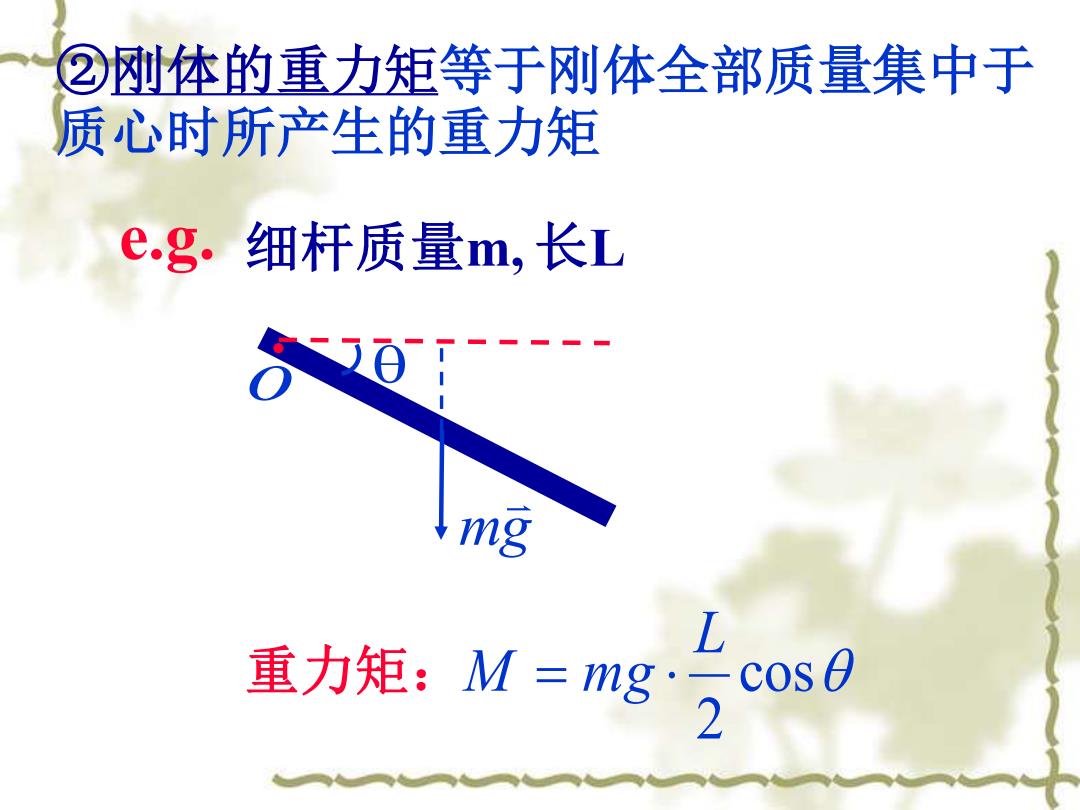
②刚体的重力矩等于刚体全部质量集中于 质心时所产生的重力矩 o mg 重力矩: cos 2 L M = mg e.g. 细杆质量m, 长L
③J=∑△mr2(Rotational inertia) 第i质元的质量 第i质元到转轴的距离 SI单位:kgm2 e.g. n 2m 02 对00'轴:J=m(径L)2+2m(3L)} 子mL乃
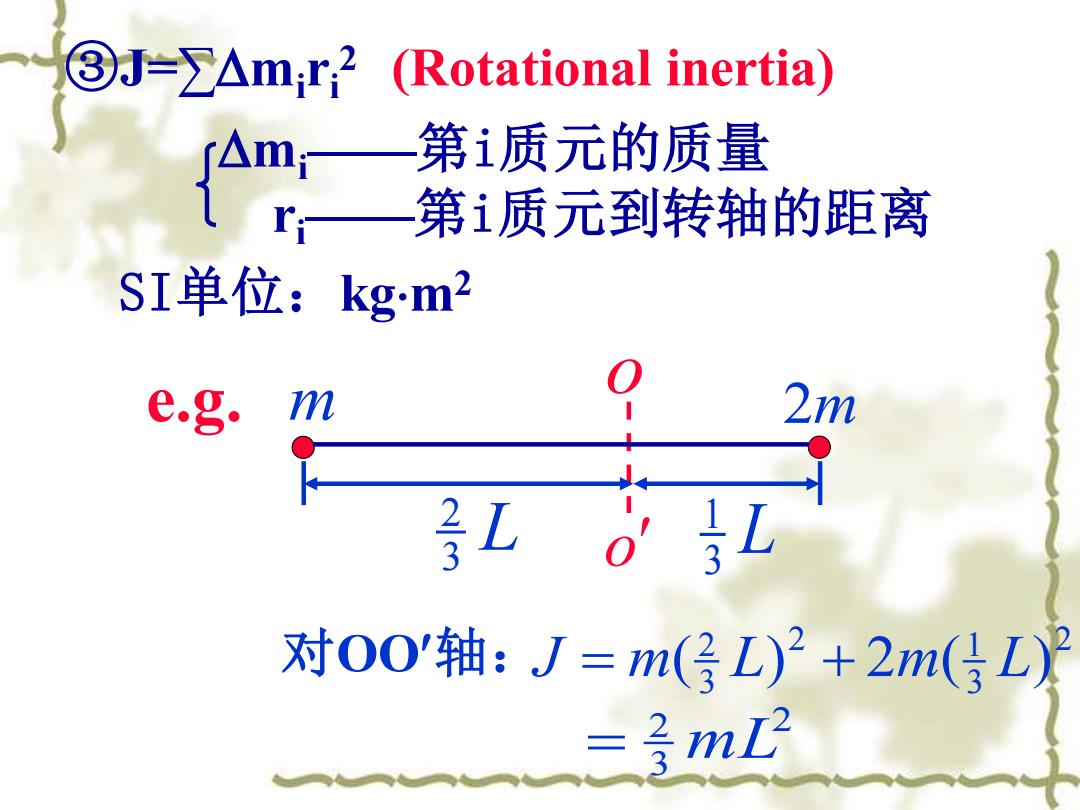
③J=∑mi ri 2 (Rotational inertia) mi——第i质元的质量 ri——第i质元到转轴的距离 e.g. o o m 2m L3 2 L3 1 2 3 = 2 mL 2 3 2 1 3 2 对OO轴: J = m( L) + 2m( L) SI单位:kgm2
)J的大小依赖于刚体质量相对于转轴的 分布 e.g. 细杆质量m,) 长L 则对于00轴,J=mL23 对于CC'轴,J=mL2/12 ii)平行轴原理 J=J。+mR2
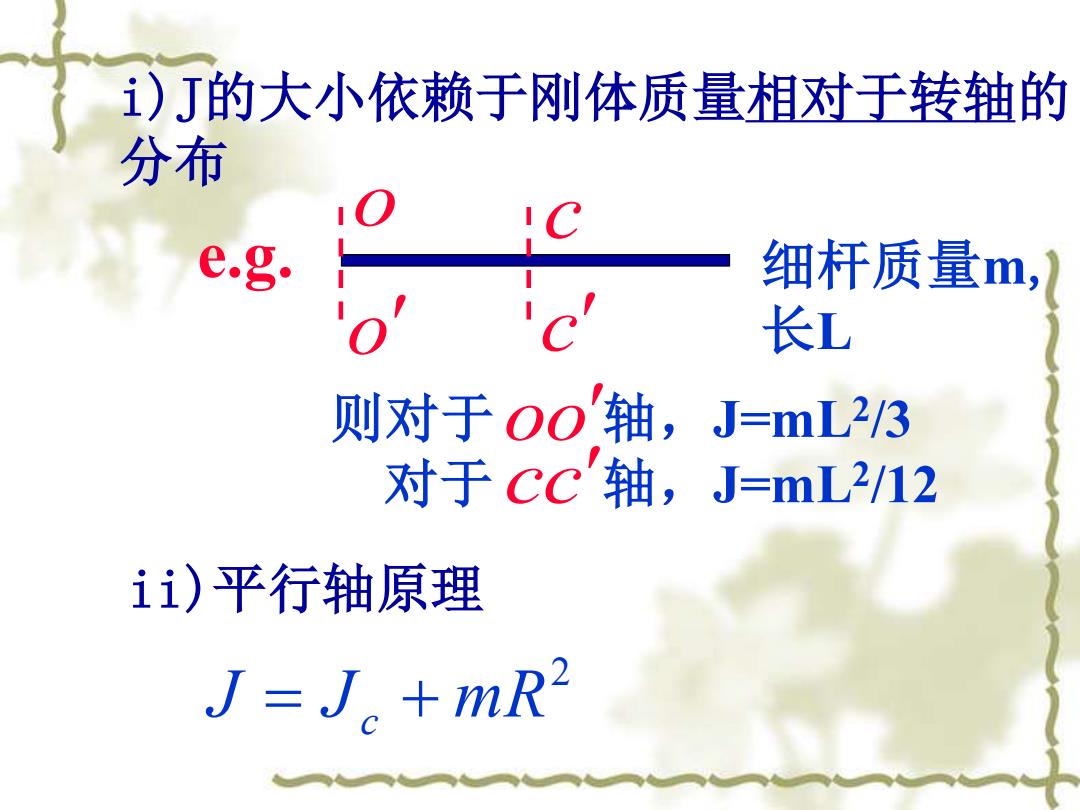
i)J的大小依赖于刚体质量相对于转轴的 分布 o o c c 细杆质量m, 长L 则对于 轴,J=mL2 /3 对于 轴,J=mL2 cc /12 oo e.g. ii)平行轴原理 2 J = Jc + mR

iii)J量度了刚体转动惯性的大小 ④转动定律与牛Ⅱ比较: F ma & ik Sis M=Ja
iii)J量度了刚体转动惯性的大小 ④转动定律与牛Ⅱ比较: M~ J ~ ~ F a m F ma = M = J