
国家重点实验室 4.1.4残留边带调制(VSB) 残留边带调制是介于SSB与DSB之间的一种调制方式, 它既克服了DSB信号占用频带宽的缺点,又解决了SSB信号 实现上的难题。在VSB中,不是完全抑制一个边带(如同 S$B中那样),而是逐渐切割,使其残留一小部分,如图4- 8(d)所示。 用滤波法实现残留边带调制的原理如图4·9(a)所示。 图中,滤波器的特性应按残留边带调制的要求来进行设计。 现在我们来确定残留边带滤波器的特性。假设HVs(o)是 所需的残留边带滤波器的传输特性。由图4-9(a)可知,残留 边带信号的频谱为
4.1.4残留边带调制(VSB) 残留边带调制是介于SSB与DSB之间的一种调制方式, 它既克服了DSB信号占用频带宽的缺点,又解决了SSB信号 实现上的难题。在VSB中,不是完全抑制一个边带(如同 SSB中那样),而是逐渐切割,使其残留一小部分,如图 4 - 8(d)所示。 用滤波法实现残留边带调制的原理如图 4 - 9(a)所示。 图中, 滤波器的特性应按残留边带调制的要求来进行设计。 现在我们来确定残留边带滤波器的特性。假设HVSB(ω)是 所需的残留边带滤波器的传输特性。由图 4 - 9(a)可知,残留 边带信号的频谱为
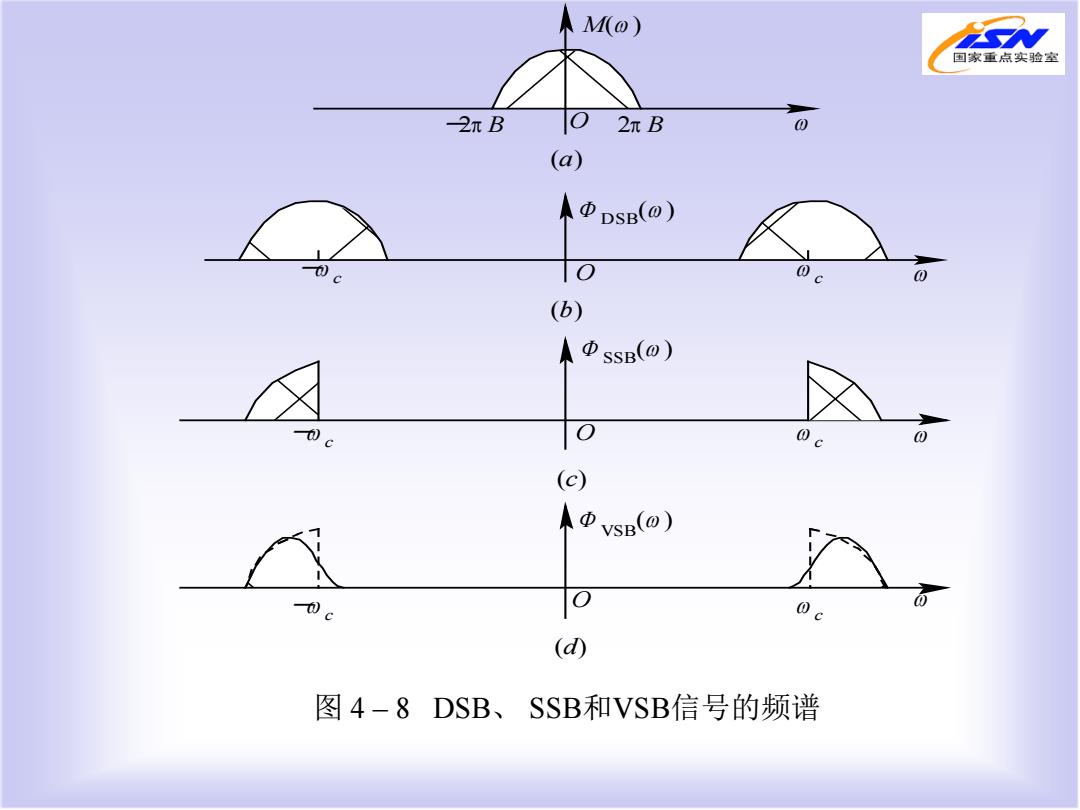
M(@) 国家重点实验室 2πB 102B (a) ADSB(O) O 00 (b) 人ΦsSB(O) o 0。 (c) ADVSB(0) @c (d) 图4-8 DSB、SSB和VSB信号的频谱
图 4 – 8 DSB、 SSB和VSB信号的频谱 M(ω ) -2π B O 2π B ω Φ DSB(ω ) -ω c O ω c (a) (b) Φ SSB(ω ) -ω c O ω ω c ω -ω c ω c Φ VSB(ω ) O ω (c) (d)
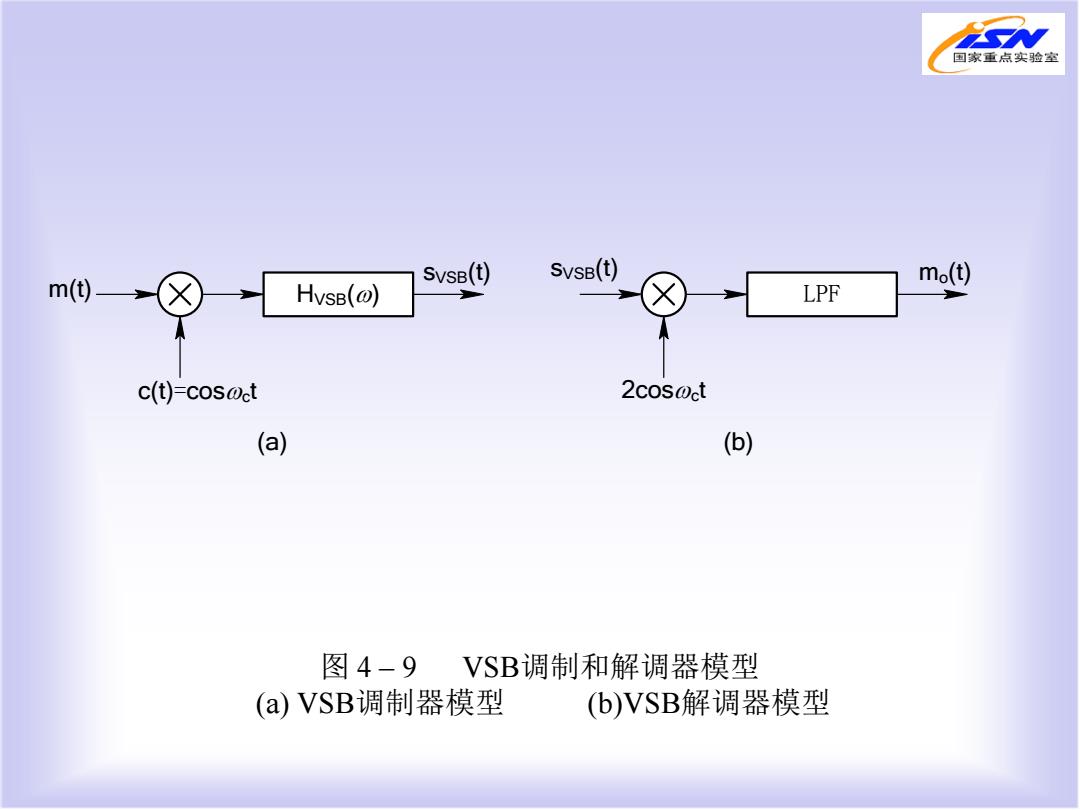
国家重点实验室 SvsB(t) SvsB(t) mo(t) m(t) HvsB(@) LPF c(t)=cos@ct 2cos@ct (a) (b) 图4-9VSB调制和解调器模型 (a)VSB调制器模型 (b)VSB解调器模型
图 4 – 9 VSB调制和解调器模型 (a) VSB调制器模型 (b)VSB解调器模型 m HVSB(ω) (t) c(t)=cosωct sVSB(t) LPF mo(t) 2cosωct sVSB(t) (a) (b)

国家重点实验室 现在我们来确定残留边带滤波器的特性。假设HVs(@)是所 需的残留边带滤波器的传输特性。由图4-9(a)可知,残留边带 信号的频谱为 Ss(@)=[M(@+0.)+M(@-0.)Hiso(0) 为了确定上式中残留边带滤波器传输特性Hvs(O)应满足 的条件,我们来分析一下接收端是如何从该信号中恢复原基带 信号的。 VSB信号显然也不能简单地采用包络检波,而必须采用如 图4-9b)所示的相干解调。图中,残留边带信号svs()与相干 载波2c0so,的乘积为
现在我们来确定残留边带滤波器的特性。假设HVSB(ω)是所 需的残留边带滤波器的传输特性。由图 4 - 9(a)可知,残留边带 信号的频谱为 为了确定上式中残留边带滤波器传输特性HVSB(ω)应满足 的条件,我们来分析一下接收端是如何从该信号中恢复原基带 信号的。 VSB信号显然也不能简单地采用包络检波, 而必须采用如 图 4 - 9(b)所示的相干解调。图中,残留边带信号sVSB(t)与相干 载波2cosωct的乘积为 1 ( ) [ ( ) ( )] ( ) 2 S M MH VSB ω ωω ωω ω = ++ − c c VSB

国家重点实验室 2svsB(t)cos@t LSvsB(@+@)+SvsB(@-@)] 将式(4.1-12)代入上式,选择合适的低通滤波器的截止频 率,消掉士2o处的频谱,则低通滤波器的输出频谱 M,(o)=M(o)[H,(o+@)+Hm(a-o,】 式告诉我们,为了保证相干解调的输出无失真地重现调 制信号m()一M(o),必须要求 Hvss(O+0。)+Hvs(O-0)=常数,O≤@g(4.1-13) 式中,Q1是调制信号的最高频率。 式(4.1-13)就是确定残留边带滤波器传输特性Hvs(o)所 必须遵循的条件。满足上式的Hvs(o)的可能形式
2sVSB(t) cosωct [SVSB(ω+ωc)+SVSB(ω-ωc)] 将式(4.1 - 12)代入上式,选择合适的低通滤波器的截止频 率,消掉±2ωc处的频谱,则低通滤波器的输出频谱 式告诉我们,为了保证相干解调的输出无失真地重现调 制信号m(t) M(ω),必须要求 HVSB(ω+ωc)+HVSB(ω-ωc)=常数,|ω|≤ωH (4.1 - 13) 式中,ωH是调制信号的最高频率。 式(4.1 - 13)就是确定残留边带滤波器传输特性HVSB(ω)所 必须遵循的条件。满足上式的HVSB(ω)的可能形式 ( ) ( ) ( ) ( ) 1 2 M MH H o ω ω ωω ωω = VSB c VSB c ++ − ⇔