
国家重点实验室 由以上表示式可见,对于幅度调制信号,在波形上,它的 幅度随基带信号规律而变化;在频谱结构上,它的频谱完全是 基带信号频谱结构在频域内的简单搬移(精确到常数因子)。由 于这种搬移是线性的,因此幅度调制通常又称为线性调制。 图4·1之所以称为调制器的一般模型,是因为在该模型 中,适当选择滤波器的特性H(©),便可以得到各种幅度调制信 号。例如,调幅(AM)、双边带(DSB)、单边带(SSB)及残留 边带(VSB)信号,下面分别介绍
由以上表示式可见,对于幅度调制信号,在波形上,它的 幅度随基带信号规律而变化;在频谱结构上,它的频谱完全是 基带信号频谱结构在频域内的简单搬移(精确到常数因子)。 由 于这种搬移是线性的,因此幅度调制通常又称为线性调制。 图 4 - 1 之所以称为调制器的一般模型, 是因为在该模型 中,适当选择滤波器的特性H(ω),便可以得到各种幅度调制信 号。例如,调幅(AM)、双边带(DSB)、单边带(SSB)及残留 边带(VSB)信号,下面分别介绍

国家重点实验室 4.1.1调幅(AM0 在图4-1中,假设h(t)=δ(t),即滤波器(H(o)=1)为全通网络, 调制信号()先叠加直流A后再与载波相乘(见图4-2),就可形成 调幅(A)信号,其时域和频域表示式分别为 Su (t)=Ao +m(t)cos@.t (4.1-3) =Aocos@t +m(t)cosot su(@)=πA,[δ0+a.)+6o-a)] +2Lo+a+K0-a】 (4.1-4) 式中,A为外加的直流分量;()可以是确知信号,也可以是 随机信号(此时,已调信号的频域表示必须用功率谱描述),但通常 认为其平均值m()=0。其波形和频谱如图4-3所示
4.1.1调幅(AM) 在图 4 - 1 中,假设h(t)=δ(t),即滤波器(H(ω)=1)为全通网络, 调制信号m(t)先叠加直流A0后再与载波相乘(见图 4 - 2), 就可形成 调幅(AM)信号,其时域和频域表示式分别为 (4.1 - 3) (4.1 - 4) 式中,A0为外加的直流分量; m(t)可以是确知信号,也可以是 随机信号(此时,已调信号的频域表示必须用功率谱描述),但通常 认为其平均值m(t) =0。其波形和频谱如图 4 - 3 所示。 ( ) ( ) ( ) AM 0 c 0 c c s t A m t cos t =A cos t m t cos t ω ω ω = + + AM ( ) 0 c c c c S A( )( ) 1 M( ) M( ) 2 ω π δω ω δω ω ωω ωω = ++ − + ++ −
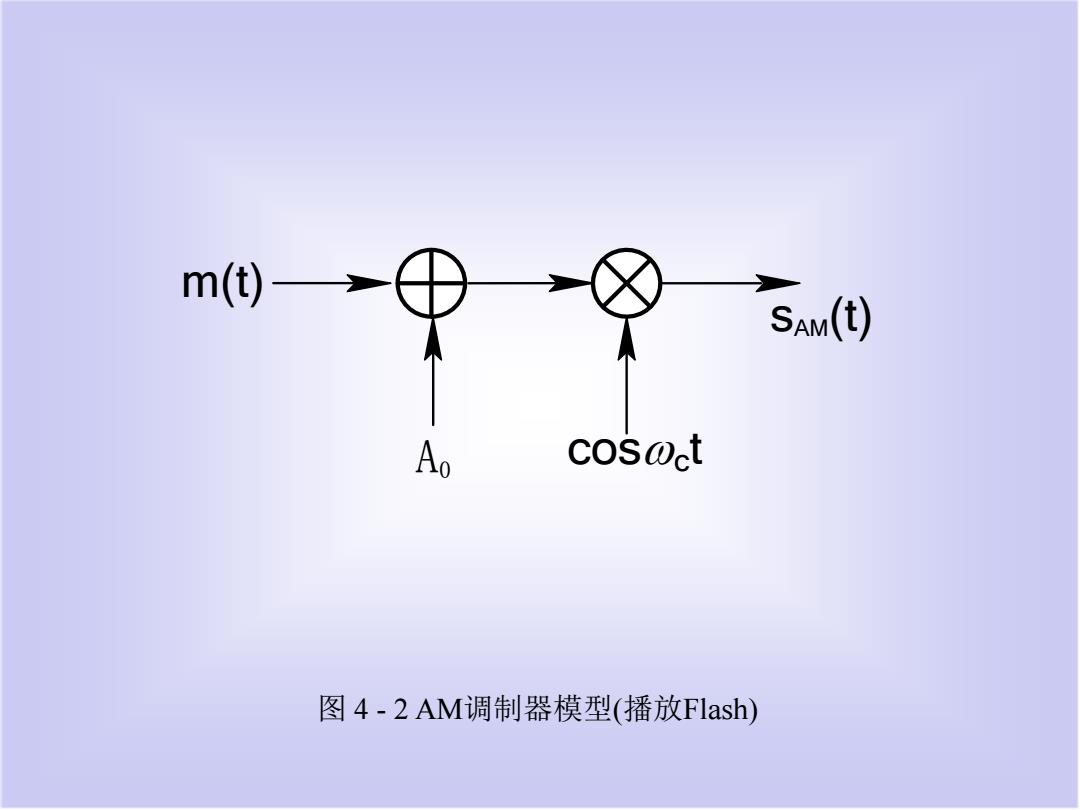
SAM(t) cos@ct 图4-2AM调制器模型(播放Flash)
图 4 - 2 AM调制器模型(播放Flash) m(t) sAM(t) A cosωct 0
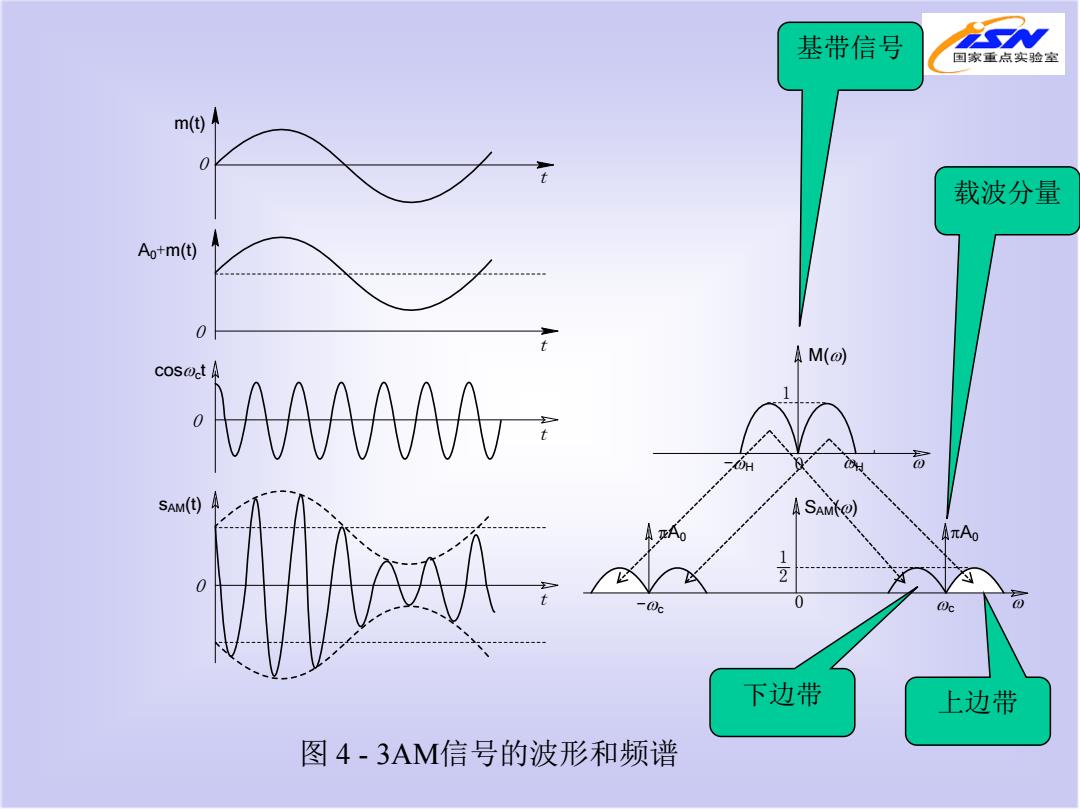
基带信号 国家重点实验室 m(t) 载波分量 Ao+m(t) AM(@) cos SAM(t) 下边带 上边带 图4-3AM信号的波形和频谱
图 4 - 3AM信号的波形和频谱 m(t) O t A0+m(t) O t O O t t cosωct sAM(t) 1 M(ω) πA0 -ωH ωH ω -ωc ωc πA0 SAM(ω) 0 2 1 ω 0 下边带 上边带 载波分量 基带信号

由图4-3的时间波形可知,当满足条件m(tma≤Ao时AM 信号的包络与调制信号成正比,所以用包络检波的方法很容易 恢复出原始的调制信号,否则,将会出现过调幅现象而产生包 络失真。这时不能用包络检波器进行解调,为保证无失真解调, 可以采用同步检波器。 由图4-3的频谱图可知,AM信号的频谱SM(o)由载频分 量和上、下两个边带组成,上边带的频谱结构与原调制信号的 频谱结构相同,下边带是上边带的镜像。因此,AM信号是带 有载波的双边带信号,它的带宽是基带信号带宽「的两倍,即 BAMF2fH
由图 4 - 3 的时间波形可知,当满足条件|m(t)|max≤A0 时AM 信号的包络与调制信号成正比,所以用包络检波的方法很容易 恢复出原始的调制信号,否则,将会出现过调幅现象而产生包 络失真。这时不能用包络检波器进行解调,为保证无失真解调, 可以采用同步检波器。 由图 4 - 3 的频谱图可知,AM信号的频谱SAM(ω)由载频分 量和上、下两个边带组成,上边带的频谱结构与原调制信号的 频谱结构相同,下边带是上边带的镜像。因此,AM信号是带 有载波的双边带信号,它的带宽是基带信号带宽fH的两倍,即 BAM =2fH