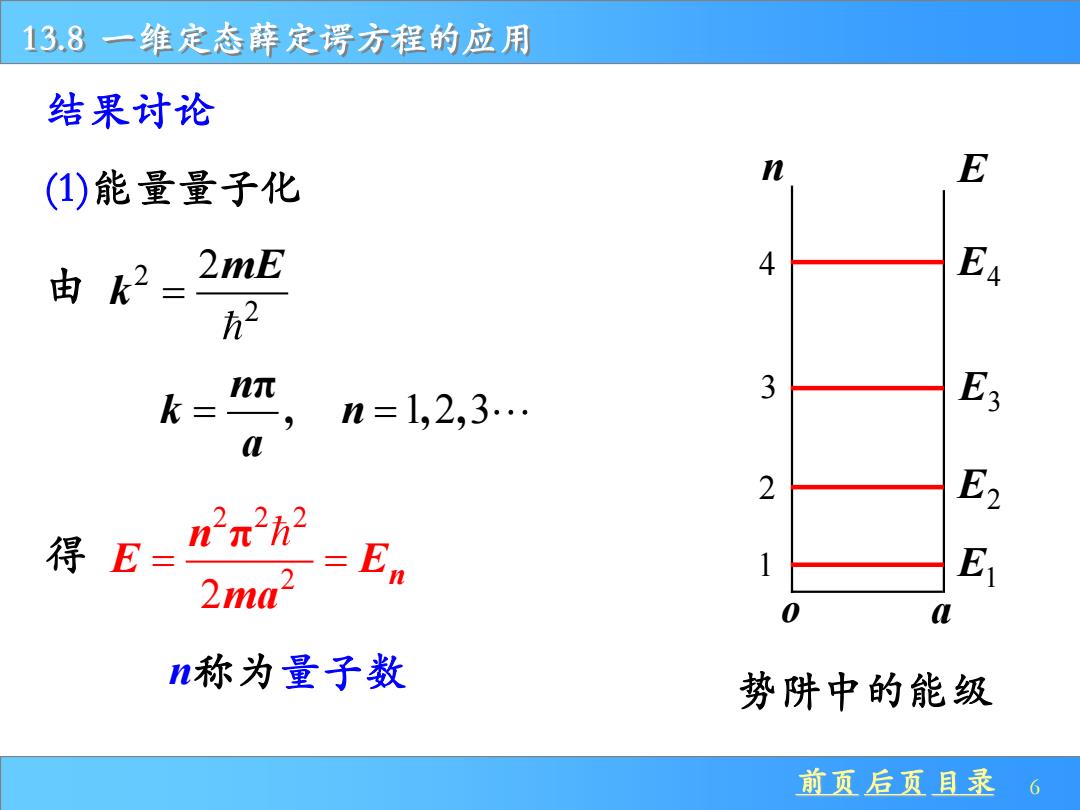
13.8一维定态薛定谔方程的应用 结果讨论 (1)能量量子化 E 由k2=2mE E 方2 k=mn 3 n=1,2,3… E E2 得E=nn2 2ma2=En E o n称为量子数 势阱中的能级 前页后页目录 6
前页 后页 目录 6 13.8 一维定态薛定谔方程的应用 结果讨论 (1)能量量子化 由 2 2 2mE k = 1 2 3 π , , , n k n a = = 得 2 2 2 2 2 π n n E E ma = = n称为量子数 E1 E2 E3 E4 o a n E 1 2 3 4 势阱中的能级

13.8一维定态薛定谔方程的应用 n2元2h2 En 2ma 能级的能量间隔 △E=Em+1-Em=(2n+l) π2h2 2 2m0 能级的能量相对间隔 △E(2n+1) →0 En n-→00 前页后页目录 7
前页 后页 目录 7 13.8 一维定态薛定谔方程的应用 能级的能量间隔 E E E = − n n +1 2 2 2 2 2 π n n E ma = 2 2 2 2 1 2 π ( ) n ma = + 能级的能量相对间隔 n E E 2 ( ) 2 1 n n + = 0 ⎯⎯⎯→ n→

13.8一维定态薛定谔方程的应用 n2π2h2 En= 2ma2 (②)最小能量不为零 E1= 元22 基态能或零点能 2ma (3)解为驻波形式 ,元 Et Ψ(x,t)= 二sin(x)eh,n=1,2,3,… 物质波在阱中形成驻波,阱壁处为波节。 前页后页目录8
前页 后页 目录 8 13.8 一维定态薛定谔方程的应用 (2)最小能量不为零 2 2 1 2 2 π E ma = 基态能或零点能 (3)解为驻波形式 物质波在阱中形成驻波,阱壁处为波节。 2 1 2 3 π ( , ) sin( )e , , , , i n Et Ψ x t x n a a − = = 2 2 2 2 2 π n n E ma =