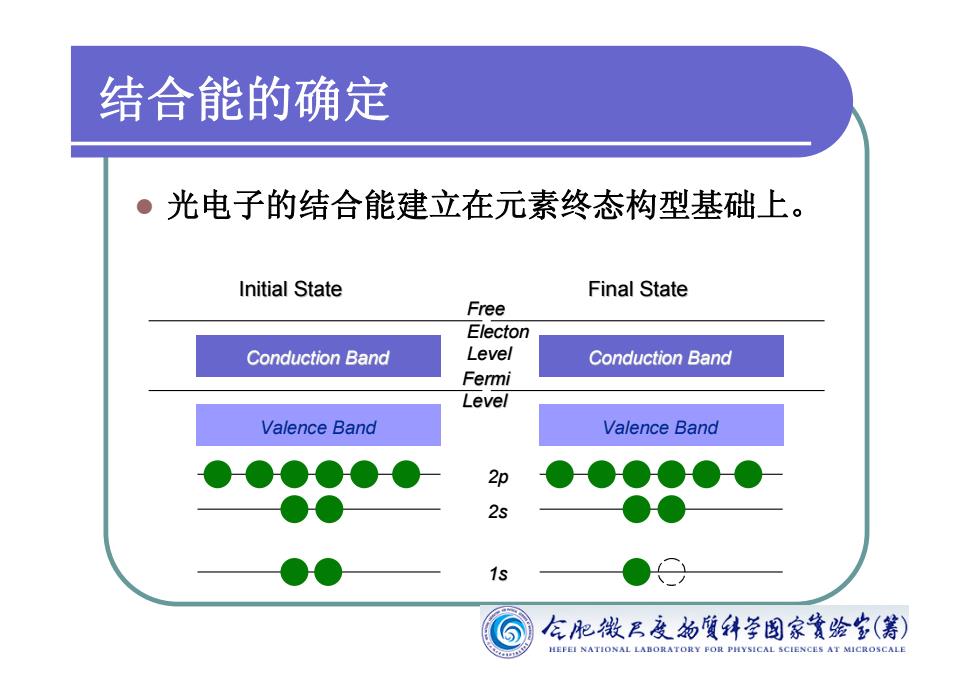
结合能的确定 。光电子的结合能建立在元素终态构型基础上。 Initial State Final State Free Electon Conduction Band Level Conduction Band Fermi Level Valence Band Valence Band 2p 2s 1s 名肥牧B度的質科学图家簧绘岁(筹) HEPEI NATIONAL LABORATOR¥FOPIHY51 CAL SCIENC里S AT MICROSCALI
结合能的确定 l 光电子的结合能建立在元素终态构型基础上。 Conduction Band Valence Band Fermi Level Free Electon Level Conduction Band Valence Band 1s 2s 2p Initial State Final State

2.1.2、结合能的理论计算 (1)、Koopmans定理(突然近似) 原子体系发射光电子后,原稳定的电子结构被破坏,这时求解状态 波函数和本征值遇到很大的理论困难。Koopmani认为在发射电子过 程中,发射过程是如此突然,以至于其它电子根本来不及进行重新 调整。即电离后的体系同电离前相比,除了某一轨道被打出一个电 子外,其余轨道电子的运动状态不发生变化,而处于一种“冻结状 态”(突然近似(Sudden Approximation))。这样,电子的结合能应 是原子在发射电子前后的总能量之差。由于终态-1个电子的能量和 空间分布与电子发射前的初态相同,则 EkT (n,L,j)=-EScF (n,1,) 此即Koopmans?定理。 ●测量的E值与计算的轨道能量有10-30eV的偏差,这是因为这种近 似完全忽略了电离后终态的影响,实际上初态和终态效应都会影响 测量的E值。这种方法只适用于闭壳层体系。 左肥微耳度的質锌学图家簧绘岁(筹) HEFEE NATIONAL LADORATORY
2.1.2、结合能的理论计算 (1)、Koopman定理(突然近似) l 原子体系发射光电子后,原稳定的电子结构被破坏,这时求解状态 波函数和本征值遇到很大的理论困难。Koopman认为在发射电子过 程中,发射过程是如此突然,以至于其它电子根本来不及进行重新 调整。即电离后的体系同电离前相比,除了某一轨道被打出一个电 子外,其余轨道电子的运动状态不发生变化,而处于一种“冻结状 态”(突然近似(Sudden Approximation))。这样,电子的结合能应 是原子在发射电子前后的总能量之差。由于终态N-1个电子的能量和 空间分布与电子发射前的初态相同,则 此即Koopmans定理。 l 测量的EB值与计算的轨道能量有10-30 eV的偏差,这是因为这种近 似完全忽略了电离后终态的影响,实际上初态和终态效应都会影响 测量的EB值 。这种方法只适用于闭壳层体系。 ( , , ) ( , , ) KT SCF EB n l j = -E n l j

(2)、绝热近似(Adiabatic Approximation 实际上初态和终态效应都会影响测量的E值。 绝热近似认为,电子由内壳层出射,结果使原来体系的 平衡场破坏,形成的离子处于激发态。其余轨道的电子 将作重新调整,电子道半径会出现收缩或膨胀,这种 电子结构的调整,称为电子弛豫。 ● 弛豫结果使离子回到基态,并释放出弛豫能δ汇ea 由于 弛豫过程大体和光电发射同时进行,所以弛豫使出射的 光电子加速,提高了光电子动能。此外,还应考虑到相 对论效应和电子相关作用,综合考虑这些效应进行修正 后得到: Eg=ET-6E,ela+δE,ela+δE.am 这样就和实验测的值符合一致了 :肥牧B度的質科学图家簧绘岁(筹) LABORATOR¥ POR PHYSICAL SCIENCES AT MICROSCALI
(2)、绝热近似(Adiabatic Approximation) l 实际上初态和终态效应都会影响测量的EB值。 l 绝热近似认为,电子由内壳层出射,结果使原来体系的 平衡场破坏,形成的离子处于激发态。其余轨道的电子 将作重新调整,电子轨道半径会出现收缩或膨胀,这种 电子结构的调整,称为电子弛豫。 l 弛豫结果使离子回到基态,并释放出弛豫能dErelax。由于 弛豫过程大体和光电发射同时进行,所以弛豫使出射的 光电子加速,提高了光电子动能。此外,还应考虑到相 对论效应和电子相关作用,综合考虑这些效应进行修正 后得到: l 这样就和实验测的值符合一致了 ad KT EB EB E relax E E relat corr = - d + + d d
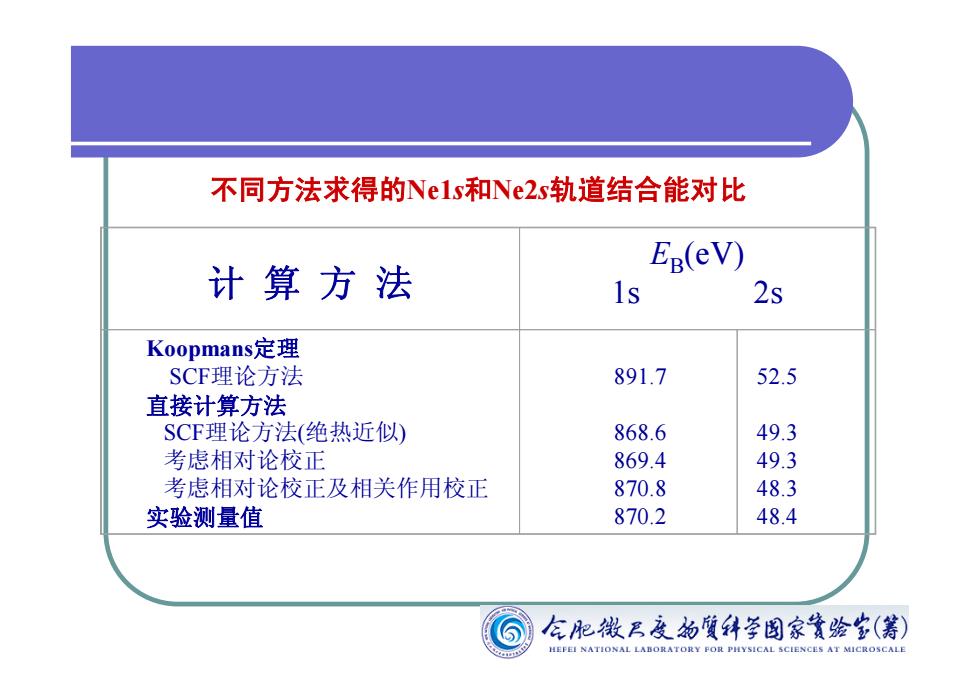
不同方法求得的Nels和Ne2s轨道结合能对比 EB(ev) 计算方法 1s 2s Koopmans定理 SCF理论方法 891.7 52.5 直接计算方法 SCF理论方法(绝热近似) 868.6 49.3 考虑相对论校正 869.4 49.3 考虑相对论校正及相关作用校正 870.8 48.3 实验测量值 870.2 48.4 左肥牧耳度的質锌学图家簧绘岁(筹) HEFEI NATIONAL LABORATORY P且PIYs1CAL5 CEENC里S AT MICROSCAL
计 算 方 法 EB (eV) 1s 2s Koopmans定理 SCF理论方法 直接计算方法 SCF理论方法(绝热近似) 考虑相对论校正 考虑相对论校正及相关作用校正 实验测量值 891.7 868.6 869.4 870.8 870.2 52.5 49.3 49.3 48.3 48.4 不同方法求得的Ne1s和Ne2s轨道结合能对比

2.2、化学位移 如方程EB=E(n-1)-E(n)所表明,初态和终态效应都对 观察的结合能E有贡献。初态即是光电发射之前原子的 基态。如果原子的初态能量发生变化,例如与其它原子化 学成键,则此原子中的电子结合能E就会改变。E的变 化△E称为化学位移。 原子因所处化学环境不同(化合物结构的变化和元素氧化 状态的变化)而引起的内壳层电子结合能变化,在谱图上 表现为谱峰有规律的位移,这种现象即为化学位移。 所谓某原子所处化学环境不同有两方面的含义:一是指与 它相结合的元素种类和数量不同:二是指原子具有不同的 化学价态。 左肥钱男度的質锌学图家簧绘當(筹) NATIONA PIHY5 ICAL SCIENC里sAI
2.2、化学位移 l 如方程EB = Ef (n-1) – Ei (n)所表明,初态和终态效应都对 观察的结合能EB 有贡献。初态即是光电发射之前原子的 基态。如果原子的初态能量发生变化,例如与其它原子化 学成键,则此原子中的电子结合能EB就会改变。EB的变 化DEB称为化学位移。 l 原子因所处化学环境不同(化合物结构的变化和元素氧化 状态的变化)而引起的内壳层电子结合能变化,在谱图上 表现为谱峰有规律的位移,这种现象即为化学位移。 l 所谓某原子所处化学环境不同有两方面的含义:一是指与 它相结合的元素种类和数量不同;二是指原子具有不同的 化学价态