
1.5.2、表面灵敏性 一 般来讲,分析方法的表面灵敏度依赖于所检测的辐射。 表面分析技术以电子能谱为中心,作为信息载体的特征 电子从被X射线照射的样品中发射出,然后到达能量分析 器和检测器进行分析测量。 ● 在X射线光电子能谱中,尽管轰击表面的X射线光子可透 入固体很深(~1μ),但由于电子在固体中的非弹性散射 截面很大,只有小部分电子保持原有特征能量而逸出表 面。可被检测的无能量损失的出射电子仅来自于表面的 1~10nm。在固体较深处产生的电子也可能逸出,但在 其逸出的路径中会与其它原子碰撞而损失能量,因而它 们对分析是无用的。电子能谱的表面灵敏性是在固体中 输运而没有被散射的短距电子的结果。 名肥牧男度的質锌学图家簧绘岁(筹) HEFEI NATIONAL LADORATORY
1.5.2、表面灵敏性 l 一般来讲,分析方法的表面灵敏度依赖于所检测的辐射。 表面分析技术以电子能谱为中心,作为信息载体的特征 电子从被X射线照射的样品中发射出,然后到达能量分析 器和检测器进行分析测量。 l 在X射线光电子能谱中,尽管轰击表面的X射线光子可透 入固体很深(~1mm),但由于电子在固体中的非弹性散射 截面很大,只有小部分电子保持原有特征能量而逸出表 面。可被检测的无能量损失的出射电子仅来自于表面的 1~10 nm。在固体较深处产生的电子也可能逸出,但在 其逸出的路径中会与其它原子碰撞而损失能量,因而它 们对分析是无用的。电子能谱的表面灵敏性是在固体中 输运而没有被散射的短距电子的结果
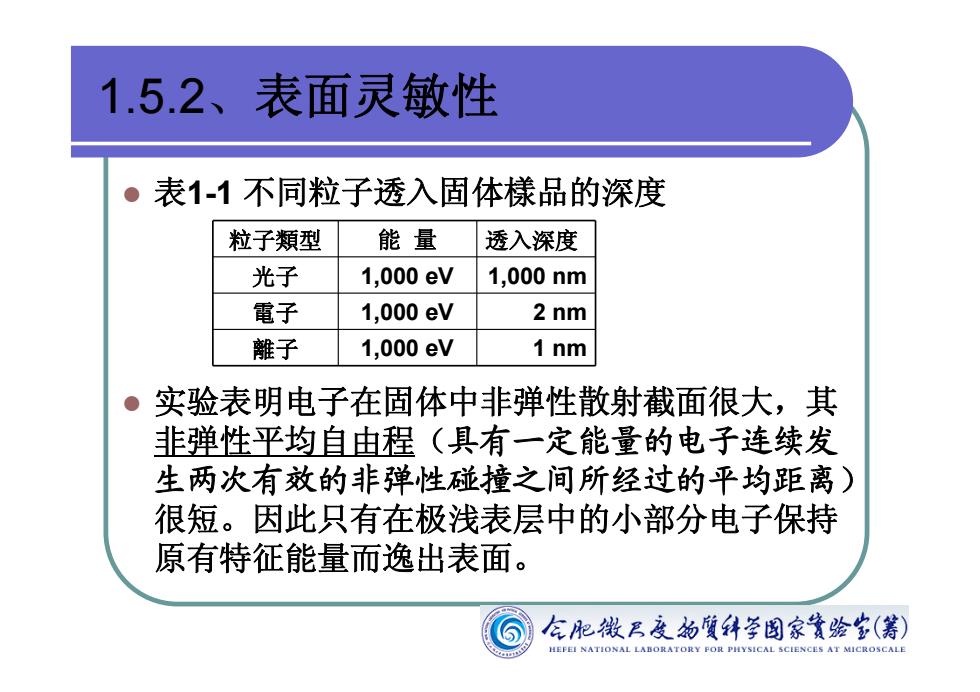
1.5.2、表面灵敏性 ● 表1-1不同粒子透入固体樣品的深度 粒子類型 能量 透入深度 光子 1,000eV 1,000nm 電子 1,000eV 2 nm 離子 1,000eV 1nm 。实验表明电子在固体中非弹性散射截面很大,其 非弹性平均自由程(具有一定能量的电子连续发 生两次有效的非弹性碰撞之间所经过的平均距离) 很短。因此只有在极浅表层中的小部分电子保持 原有特征能量而逸出表面。 左肥钱男度的質锌学图家簧绘岁(筹) NATIONA ICAL SCIENC里sAT
1.5.2、表面灵敏性 l 表1-1 不同粒子透入固体樣品的深度 l 实验表明电子在固体中非弹性散射截面很大,其 非弹性平均自由程(具有一定能量的电子连续发 生两次有效的非弹性碰撞之间所经过的平均距离) 很短。因此只有在极浅表层中的小部分电子保持 原有特征能量而逸出表面。 粒子類型 能 量 透入深度 光子 1,000 eV 1,000 nm 電子 1,000 eV 2 nm 離子 1,000 eV 1 nm

表面灵敏性术语 对于电子在物质中的输运,用不同的术语定义表面灵敏度。 MFP(入)一非弹性平均自由程。具有一定能量的电子连续发生两次 有效的非弹性碰撞之间所经过的平均距离(单位),称为电子的韭 弹性平均自由程,在表面分析中是一个重要参数,它与电子能量和 表面材料有关,它可用来估计具有不同特征能量的电子所携带的信 息深度。 ED一逃逸深度。电子由于非弹性过程无大的能量损失逃逸的几率 降到其原来值的e(38%)处垂直于表面的距离(nm单位)。 AT一衰减长度。从一特殊模型中得到的具有一定能量的电子连续 发生两次有效的非弹性碰撞之间所经过的平均距离(nm单位),这里 弹性电子散射假设是可忽略的。 SD一采样深度=3λ。(检测到的电子的百分比为95%时的信息深 度)。 对于能量在100~1000eV的电子来说,非弹性散射平均自由程的典型 值在13nm的量级,此一距离对大多数材料而言约为10个原子单层 名肥牧男度的質学图家簧绘岁(筹)
对于电子在物质中的输运,用不同的术语定义表面灵敏度。 l IMFP(λ) — 非弹性平均自由程。具有一定能量的电子连续发生两次 有效的非弹性碰撞之间所经过的平均距离(nm单位),称为电子的非 弹性平均自由程,在表面分析中是一个重要参数,它与电子能量和 表面材料有关,它可用来估计具有不同特征能量的电子所携带的信 息深度。 l ED — 逃逸深度。电子由于非弹性过程无大的能量损失逃逸的几率 降到其原来值的e -1(38%)处垂直于表面的距离(nm单位)。 l AT — 衰减长度。从一特殊模型中得到的具有一定能量的电子连续 发生两次有效的非弹性碰撞之间所经过的平均距离(nm单位),这里 弹性电子散射假设是可忽略的。 l SD — 采样深度=3λ。(检测到的电子的百分比为95%时的信息深 度)。 l 对于能量在100~1000eV的电子来说,非弹性散射平均自由程的典型 值在1~3nm的量级,此一距离对大多数材料而言约为10个原子单层。 表面灵敏性术语

第2章结合能与化学位移 1 结合能理论 2. 化学位移 3. 终态效应 4. 结合能的参考基准 左肥徵男度的質锌学图家簧绘出(筹) HEPEI NATIONAL LABORATOR¥FOPIHY51 CAL SCIENC里S AT MICROSCALI
第2章 结合能与化学位移 1. 结合能理论 2. 化学位移 3. 终态效应 4. 结合能的参考基准

2.1、结合能理论 2.1.1、结合能原理: 电子的结合能(E)代表了原子中电子(,l,s)与核电荷(Z)之间的相互作用 强度,可用PS直接实验测定,也可用量子化学从头计算方法进行计算。 理论计算结果可以和XPS测得的结果进行比较,更好地解释实验现象。 1200 ●电子的结合能是原子体系的初态 1100 (原子有n个电子)和终态(原子有 1000 n-1个电子(离子)和一自由光电子) 900 间能量的简单差。 800 EB=E/(n-1)-Ei(n) 700 600 ●若无伴随光电发射的弛豫存在, 500 则 400 EB=-轨道能量, 300 它可用非相对论的Hartree-Fock自 200 洽场(HF-SCF)方法计算出来。 100 0 20 30 40 01 60708090 100 形微君及物圆轩孕倒冢賞验玉(筹) HEFEI NATIONAL LABORATORY FOR PHYSICAL SCIENCES AT MICROSCALE
2.1、结合能理论 2.1.1、结合能原理: 电子的结合能(EB )代表了原子中电子(n,l,s)与核电荷(Z)之间的相互作用 强度,可用XPS直接实验测定,也可用量子化学从头计算方法进行计算。 理论计算结果可以和XPS测得的结果进行比较,更好地解释实验现象。 l 电子的结合能是原子体系的初态 (原子有n个电子)和终态(原子有 n-1个电子(离子)和一自由光电子) 间能量的简单差。 EB = Ef (n-1) – Ei (n) l 若无伴随光电发射的弛豫存在, 则 EB = −轨道能量, 它可用非相对论的Hartree-Fock自 洽场(HF-SCF)方法计算出来