
■超电势定义:(取超电势为正值) 2.3RT 阳极反应 1 no=0-9=-BnF ← 2.3RT g je+ g (13) BnF 2.3RT 阴极反应门R=2-0= Ig jc+ 2.3RT Ig j (14) anF anF 1在电势标的零点,即反应体系为平衡电位下,有。=力。, 因此 上式中,可用代替。和。,称为“交换电流密度”。 上一内容 下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 ■超电势定义:(取超电势为正值) 阳极反应 阴极反应 → → = − = − + = − = − + j nF RT j nF RT j nF RT j nF RT R e e O e e lg 2.3 lg 2.3 lg 2.3 lg 2.3 (13) (14) ■在电势标的零点,即反应体系为平衡电位下,有 ,因此 上式中,可用 代替 和 ,称为“交换电流密度” 。 → e = e j j 0 j → e j e j
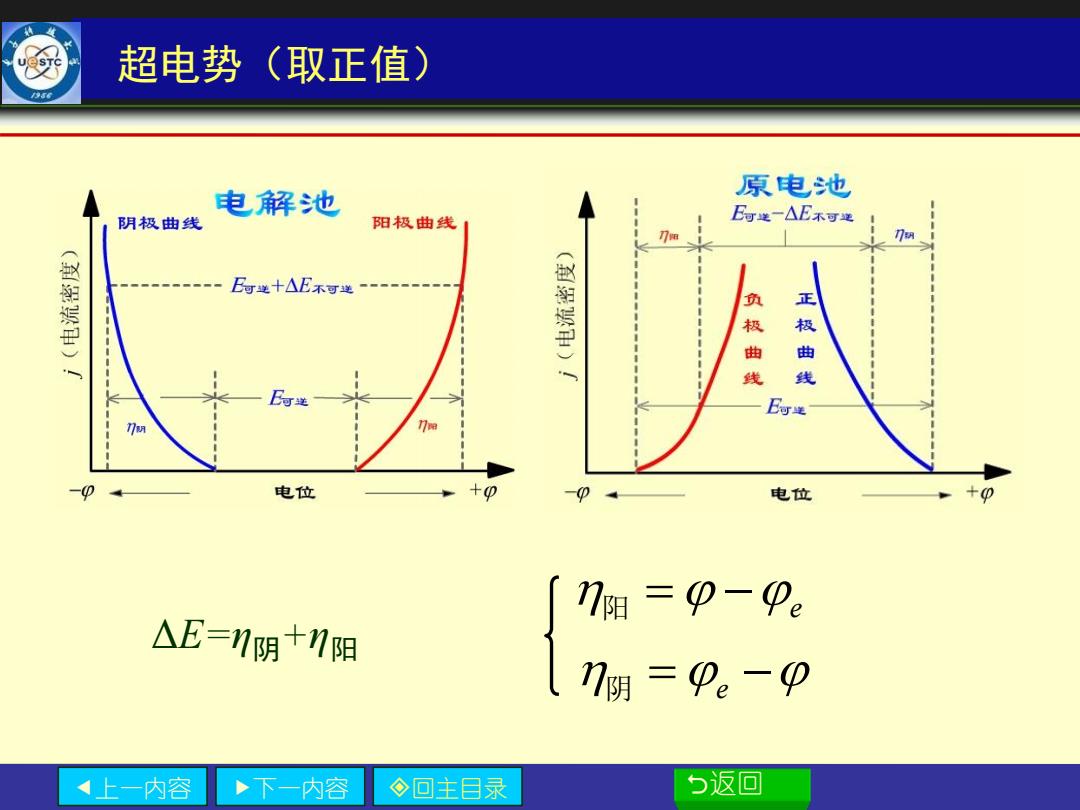
超电势(取正值) 电解池 原电池 阴极曲线 阳极曲线 E可送一△E不可递 刀e n E句送十△E不可送 《利纯联) 正 极 极 曲 线 线 E时递 7 电位 电位 -0 「7阳=φ-Pe △E=1阴十1阳 7阴=9。-p 上一内容 下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 超电势(取正值) ΔE=η阴+η阳 阳 = − e 阴 = − e

则: 2.3RT 2.3RT ←- 2.3RT 7o= gj°+ lg j= (15) BnF BnF BnF 2.3R 2.3R7 2.3RT (16) 7R=- anF g onF anF g 若将上式改写成指数形式,有: BnF (17) 10 绝对电流密度 (18) ■若知道传递系数和平衡电位这两个基本参数,便可计算任意电势下的 绝对电流密度。 上一内容 下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 则: 0 0 0 0 lg 2.3 lg 2.3 lg 2.3 lg 2.3 lg 2.3 lg 2.3 j j nF RT j nF RT j nF RT j j nF RT j nF RT j nF RT R O → → = − + = = − + = (15) (16) 若将上式改写成指数形式,有: = = → R O RT nF j j RT nF j j exp exp 0 0 (17) (18) 绝对电流密度 ■若知道传递系数和平衡电位这两个基本参数,便可计算任意电势下的 绝对电流密度
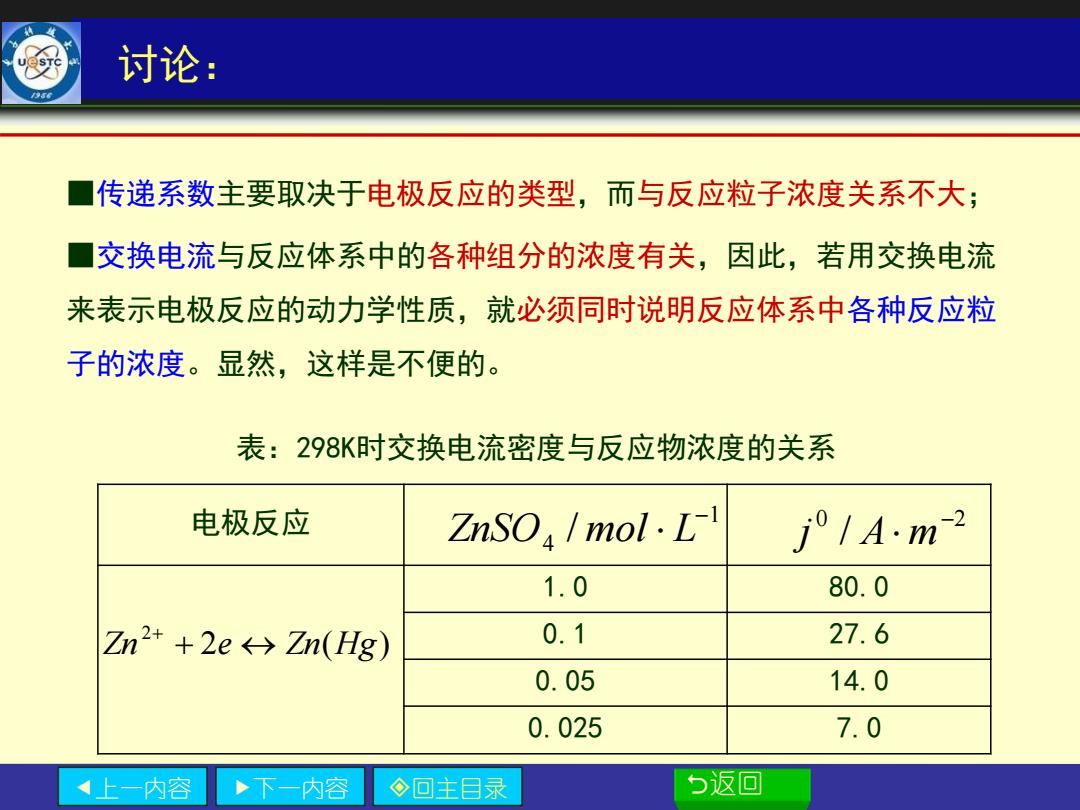
讨论: ■传递系数主要取决于电极反应的类型,而与反应粒子浓度关系不大; ■交换电流与反应体系中的各种组分的浓度有关,因此,若用交换电流 来表示电极反应的动力学性质,就必须同时说明反应体系中各种反应粒 子的浓度。显然,这样是不便的。 表:298K时交换电流密度与反应物浓度的关系 电极反应 ZnSO,mol.L j°1Am2 1.0 80.0 Zn2++2e←→Zn(Hg) 0.1 27.6 0.05 14.0 0.025 7.0 上一内容 下一内容 ◇回主目录 5返▣
上一内容 下一内容 回主目录 返回 讨论: ■传递系数主要取决于电极反应的类型,而与反应粒子浓度关系不大; ■交换电流与反应体系中的各种组分的浓度有关,因此,若用交换电流 来表示电极反应的动力学性质,就必须同时说明反应体系中各种反应粒 子的浓度。显然,这样是不便的。 表:298K时交换电流密度与反应物浓度的关系 1 4 / − ZnSO mol L 0 2 / − j A m 2 ( ) 2 Zn + e Zn Hg + 电极反应 1.0 80.0 0.1 27.6 0.05 14.0 0.025 7.0

③电极反应速度常数(K) 问题:由于交换电流与反应物浓度有关,为了使基本参数具有广泛 的适用性,能否用电极反应速度常数K来代替交换电流? ■ 当电极电位为氧化还原体系(O/R)的标准平衡电位时,即:0=0。 将其代入(5)、(6)式,得: j=nFKC.exp (19) j-wrk2C.op-nFk.c. (20) 若C。=C。,则p=p。,此时体系处于平衡状态,此时有:j=j 代入(19)、(20)式,必有:K。=K。=K 上一内容 下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 ③电极反应速度常数(K) 问题:由于交换电流 与反应物浓度有关,为了使基本参数具有广泛 的适用性,能否用电极反应速度常数 K 来代替交换电流? 0 j ■当电极电位为氧化还原体系(O/R)的标准平衡电位时,即: 将其代入(5)、(6)式,得: o =e c c e c c a a e a a nFK C RT nF j nFK C nFK C RT nF j nFK C = = − = = → 0 0 0 0 exp exp (19) (20) 若 ,则 ,此时体系处于平衡状态,此时有: 代入(19)、(20)式,必有: Ca = Cc =e → j = j Ka = Kc = K