五、反应阈能(E)与活化能E,(T)、指前因 子A(T)的关系 由定义:E,≡RT2dnk(T) dT 将:kon①)=d 8RT exp(- RT 代入上式 E=RT7+R)=E+R灯
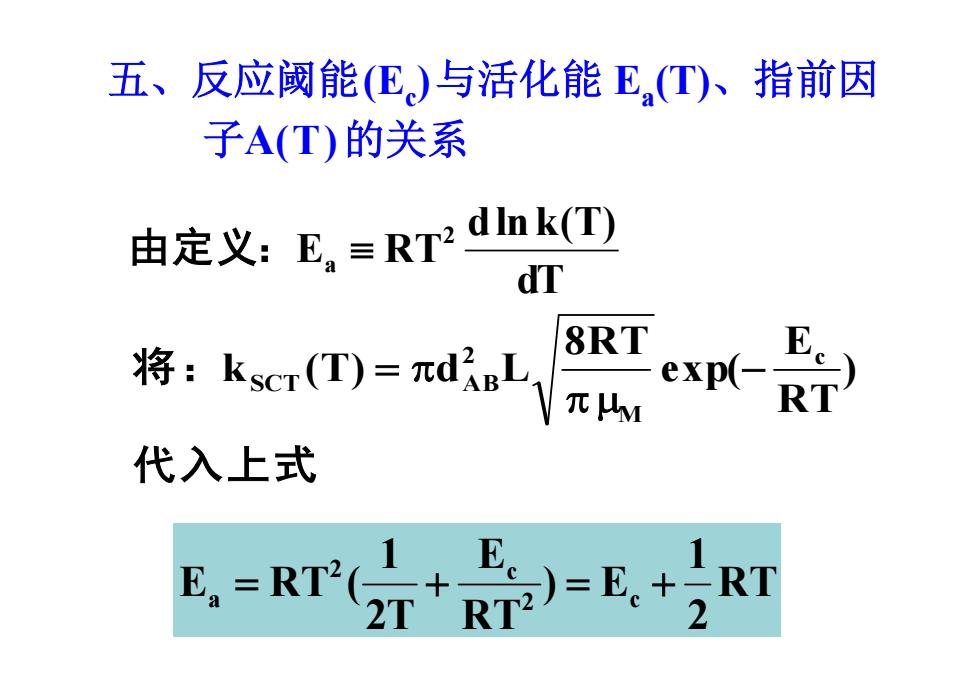
五、反应阈能(Ec )与活化能 Ea (T)、指前因 子A(T)的关系 dT dlnk(T) E RT2 由定义: a RT 2 1 ) E RT E 2T 1 E RT ( 2 c 2 c a 代入上式 将: ) RT E exp( 8RT k (T) d L c M 2 SCT AB

由定义:A(T)=k(T)eE,RT =kscr(T).e Ee+2RT)/RT 8RT.e → A(T)=πdL 元hM (Arrhe nius指前因子,e=2.718)
RT)/ RT 2 1 (E SCT E / RT c a k (T) e 由定义:A(T) k(T)e M 2 AB 8RT e A(T) d L (Arrhenius 指前因子,e 2.718)
则: 8RTe k(T)=πdRL exp(- 元M RT 注意此k(T)表达式与ksCT(T)的不同,指 数项含活化能E
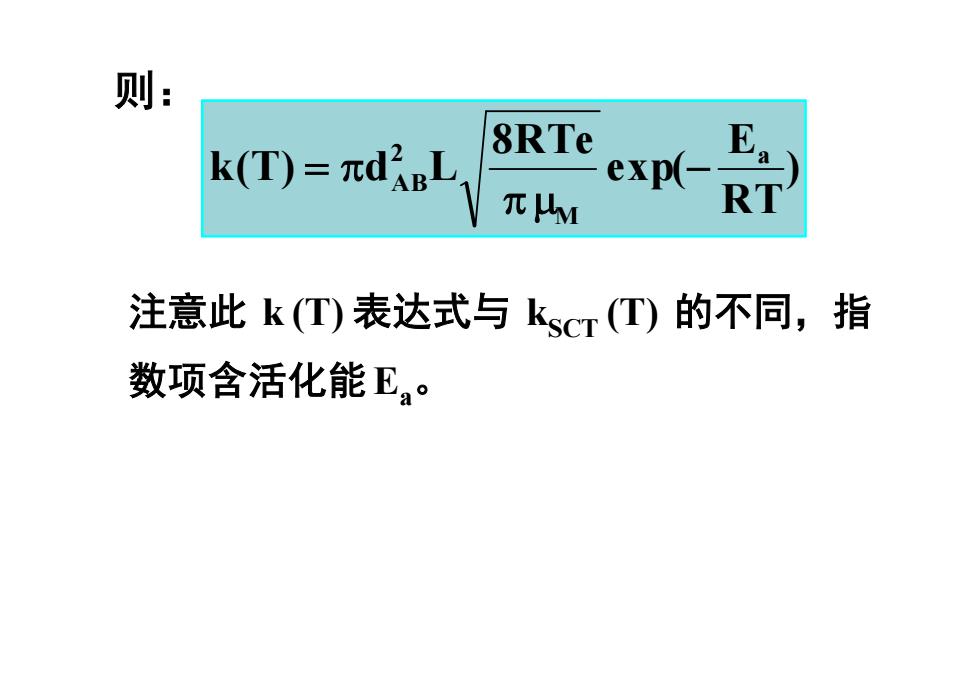
) RT E exp( 8RTe k(T) d L a M 2 AB 则: 注意此 k (T) 表达式与 kSCT (T) 的不同,指 数项含活化能Ea

讨论: E。=E+RT 1)因为hRT≈2kJ/mol(500K时) <<E。(~100kJ/mol) 所以可以认为E。≈Ea,E。很接近于活化能Ea。 2)简单碰撞理论(SCT)不能给出阈能E。的 计算方法,但能给出Arrhenius指前因子 A(T): 并且得到:AcT12
讨论: 1)因为 ½ RT 2 kJ /mol (500K时) Ec (~ 100 kJ / mol) 所以可以认为 Ec Ea ,Ec 很接近于活化能 Ea 。 RT 2 1 Ea Ec 2)简单碰撞理论(SCT)不能给出阈能 Ec 的 计算方法,但能给出 Arrhenius 指前因子 A(T): 并且得到: A T1/2

A(T)=πdL 8RT.e 元hM ■当T=800K,T12=28.28; ■当T=810K,T12=28.46;△A/A≈0.64% ■这与升温10°C反应速率k成倍增长相比可忽略 不计。这说明在一定的高温时,指前因子A(T) 对T并不敏感。 ■而且由于SCT本身比较粗糙,因此AcT12这一 预言关系在定量上是很粗糙的
当T = 800 K,T1/2 = 28.28; 当 T = 810 K,T1/2 = 28.46;A/A 0.64% 这与升温 10C 反应速率 k 成倍增长相比可忽略 不计。这说明在一定的高温时,指前因子A (T) 对T并不敏感。 而且由于SCT 本身比较粗糙,因此 A T 1/2 这一 预言关系在定量上是很粗糙的。 M 2 AB 8RT e A(T) d L