中国科学技术大学：《电磁学》课程教学资源（课件讲稿）第六章 静磁场中的磁介质

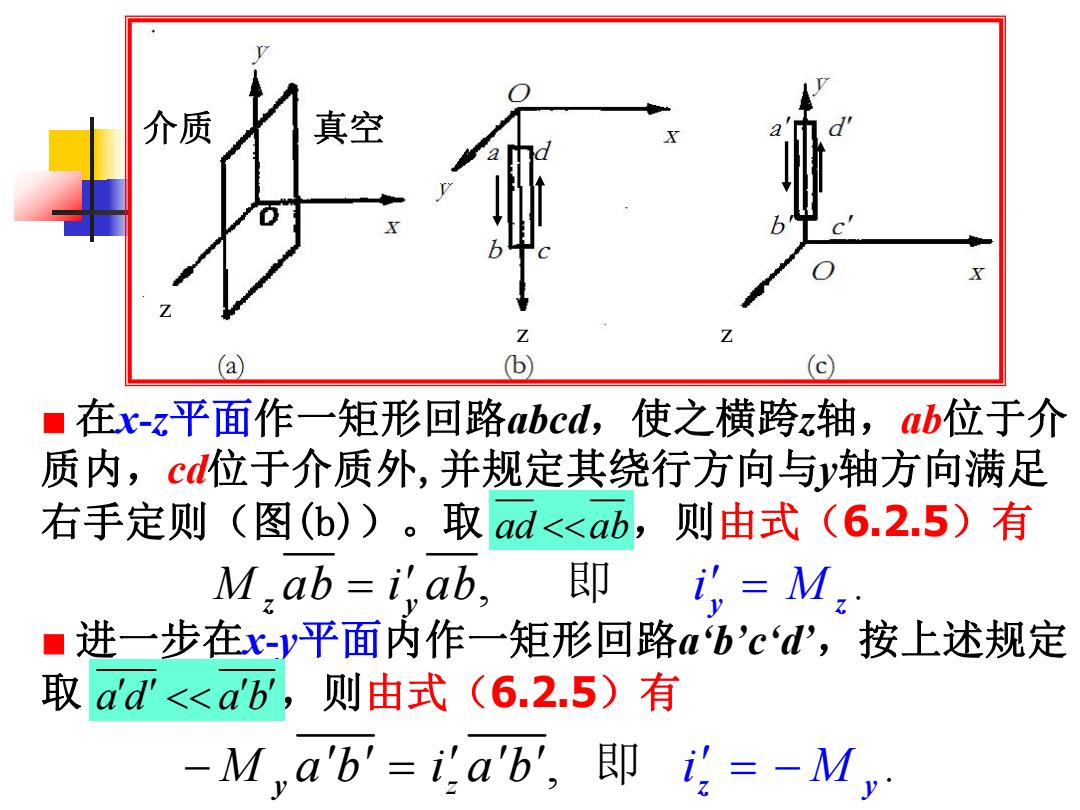
介质 真空 Z ( (b) (c ■在x-z平面作一矩形回路abcd,使之横跨z轴，ab位于介 质内，c位于介质外，并规定其绕行方向与y轴方向满足 右手定则（图(b))。取ad<<ab,则由式(6.2.5）有 M.ab=i'ab. 即 =M,. ■进一步在x-y平面内作一矩形回路ab'c‘d',按上述规定 取add<<ab,则由式(6.2.5)有 -M,a'b=iab,即=-My

z z z ■ 在x-z平面作一矩形回路abcd，使之横跨z轴，ab位于介 质内，cd位于介质外,并规定其绕行方向与y轴方向满足 右手定则（图(b)）。取 ad ab，则由式（6.2.5）有 M ab  i ab, 即 i  M . z y y z ■ 进一步在x-y平面内作一矩形回路a‘b’c‘d’ ，按上述规定 取 a d  a b ，则由式（6.2.5）有        , 即    . M z y a b i a b i z M y 介质 真空

上述磁化面电流和表面磁化强度之间的分量关系可归 纳为如下矢量关系： i'=Mxn (6.2.6) 式中为介质表面单位外法向矢量，此处即x轴的方向

上述磁化面电流和表面磁化强度之间的分量关系可归 纳为如下矢量关系： i  Mn (6.2.6) 式中n为介质表面单位外法向矢量，此处即x轴的方向

§6.3 磁介质中静磁场的基本定理 磁介质的全部作用在于提供磁化电流作为附加场源 设由传导电流和磁化电流产生的磁感应强度分别为B 和B',则总磁感应强度为 B=B。+B' (6.3.1) 显然，B应满足真空中静磁场的高斯定理和安培环路 定理： .dS=0 (6.3.2) ∮，BL=1+4,21, (6.3.3) 穿乳 穿乳 只要已知传导电流1和磁化电流的分布，就可决定 磁介质内、外的静磁场

§6.3 磁介质中静磁场的基本定理 磁介质的全部作用在于提供磁化电流作为附加场源。 设由传导电流和磁化电流产生的磁感应强度分别为 和 B' ，则总磁感应强度为 B0 0 B  B  B. (6.3.1) 显然，B应满足真空中静磁场的高斯定理和安培环路 定理：   0  S B dS (6.3.2) (6.3.3) 只要已知传导电流 和磁化电流I‘ 的分布，就可决定 磁介质内、外的静磁场。 0 I 0 0 0 . L d  I   I  ' Β L = 穿L 穿L

[例6.4]求沿轴均匀磁化的磁介质圆棒轴线上的磁场 分布。设圆棒长为l,半径为R,磁化强度为M。 [解]由于是沿轴向均匀磁化，MW轴，故磁化电流只 分布于介质棒的侧面，其面电流密度为'=M 这种电流分布与一有限长直螺线管电流等效。照 搬例5.4的结果（令三），可推得磁介质圆棒轴 线上距左端(1处的磁感应强度为： g=4 (cosB.-cosB)= M 2R+R+ 式中)=1-1。对细长棒(1>R),端点（化=0）处， B'=4oM/2;棒内远离端点处B≈4M。对圆薄片 (1<R),B'=4Ml/(2R)≈0

[例6.4] 求沿轴均匀磁化的磁介质圆棒轴线上的磁场 分布。设圆棒长为l，半径为R，磁化强度为M。 [解] 由于是沿轴向均匀磁化， M// 轴，故磁化电流只 分布于介质棒的侧面，其面电流密度为 。 这种电流分布与一有限长直螺线管电流等效。照 搬例5.4的结果（令 ），可推得磁介质圆棒轴 线上距左端 l 1处的磁感应强度为： i  M nI  i 0 0 1 2 2 1 2 2 2 2 1 2 (cos cos ) , 2 2 nI M l l B R l R l                    式中 。对细长棒( )，端点 处， ；棒内远离端点处 。对圆薄片 ( )， 。 2 1 l ll l  R 1 (l  0) B  0M / 2 B 0M l  R B  0Ml /(2R)  0

■大多数情况下问题并非如此简单。这是因为磁介质 在外磁场中磁化，磁化后的介质又会改变空间的磁场 分布，并反过来影响磁介质的磁化状态。这种相互牵 制的关系使我们难以自洽地决定介质的磁化强度或磁 化电流的分布。 ■ 类似情况在第二章2.6节讨论电介质时也曾碰到过。 当时我们的做法是引入电位移矢量。对于磁介质中的 静磁场，将式（6.2.5)代入式（6.3.3)得： ∮.BL=4+4fMdl∮.cB-ML- 穿乳 穿乳 B H=-M (6.3.4) 立即得： ∮HdL=∑。 (6.3.5) 穿引

■ 大多数情况下问题并非如此简单。这是因为磁介质 在外磁场中磁化，磁化后的介质又会改变空间的磁场 分布，并反过来影响磁介质的磁化状态。这种相互牵 制的关系使我们难以自洽地决定介质的磁化强度或磁 化电流的分布。 ■ 类似情况在第二章2.6节讨论电介质时也曾碰到过。 当时我们的做法是引入电位移矢量。对于磁介质中的 静磁场，将式（6.2.5）代入式（6.3.3）得： 令： 0 ,    B H M (6.3.4) 立即得： (6.3.5) 0 0 0 0 0 ( ) . L L L d  I  d d I      ;   Β Β L = M  L  Μ  L = 穿L 穿L 0 L d I  H  L = 穿L