
则定义: M ∑分子 (6.2.1) △V 为磁化强度。磁化强度为矢量,其方向代表磁化的方 向,其大小代表磁化的程度。在非磁化状态下,或分 子固有磁矩为零,或分子磁矩的取向杂乱无章,以 至》分子=0。于是,M=0表示磁介质处于非磁化态。 二、磁化电流 在磁化状态下,由于分子电流的有序排列,磁介 质中将出现宏观电流,称为磁化电流。其特点是: 1.磁化电流的产生不伴随电荷的宏观位移。相 反,凡伴随电荷的宏观位移的电流称为传导电流,例 如载流导体中的电流;
则定义: V m M 分子 (6.2.1) 为磁化强度。磁化强度为矢量,其方向代表磁化的方 向,其大小代表磁化的程度。在非磁化状态下,或分 子固有磁矩为零,或分子磁矩的取向杂乱无章,以 至 。于是, 表示磁介质处于非磁化态。 二、磁化电流 m分子 0 M 0 在磁化状态下,由于分子电流的有序排列,磁介 质中将出现宏观电流,称为磁化电流。其特点是: 1. 磁化电流的产生不伴随电荷的宏观位移。相 反,凡伴随电荷的宏观位移的电流称为传导电流,例 如载流导体中的电流;

2.磁化电流可存在于一切磁介质(包括绝缘体 和导体)中,不具有焦耳热效应;传导电流则只能存 在于导体(包括半导体和电离气体)中,具有焦耳热 效应。 尽管两种电流在产生机制和热效应方面存在区别, 但在激发磁场和受磁场作用方面却是完全等效的。 三、磁化电流与M的关象:既然磁化电流的出 现是物质磁化的结果,它和磁化强度之间应该存在一 定关系。为分析这种关系,我们引入分子平均磁矩m, 其定义如下: ∑m分子 (6.2.2) n△V 式中n为分子数密度
2. 磁化电流可存在于一切磁介质(包括绝缘体 和导体)中,不具有焦耳热效应;传导电流则只能存 在于导体(包括半导体和电离气体)中,具有焦耳热 效应。 ■ 尽管两种电流在产生机制和热效应方面存在区别, 但在激发磁场和受磁场作用方面却是完全等效的。 三、磁化电流与M的关系:既然磁化电流的出 现是物质磁化的结果,它和磁化强度之间应该存在一 定关系。为分析这种关系,我们引入分子平均磁矩ma, 其定义如下: , a n V m m 分子 (6.2.2) 式中n为分子数密度
这样,式(6.2.1)变成: M =nma. (6.2.3) 进一步设m。由一等效分子电流所产生,其电流强度为 I。,面积矢量为Sa,则:m。=IaSa· (6.2.4) 研究磁化电流与M的关系。假定介质中,全部分子 具有同一磁矩m。,考虑磁介质中任一闭合回路L和以它 为周线的曲面S,通过S的总磁化电流设为',其正向 与回路L的绕行方向满足右手定测(见下图(a))。 (a) (b) (c
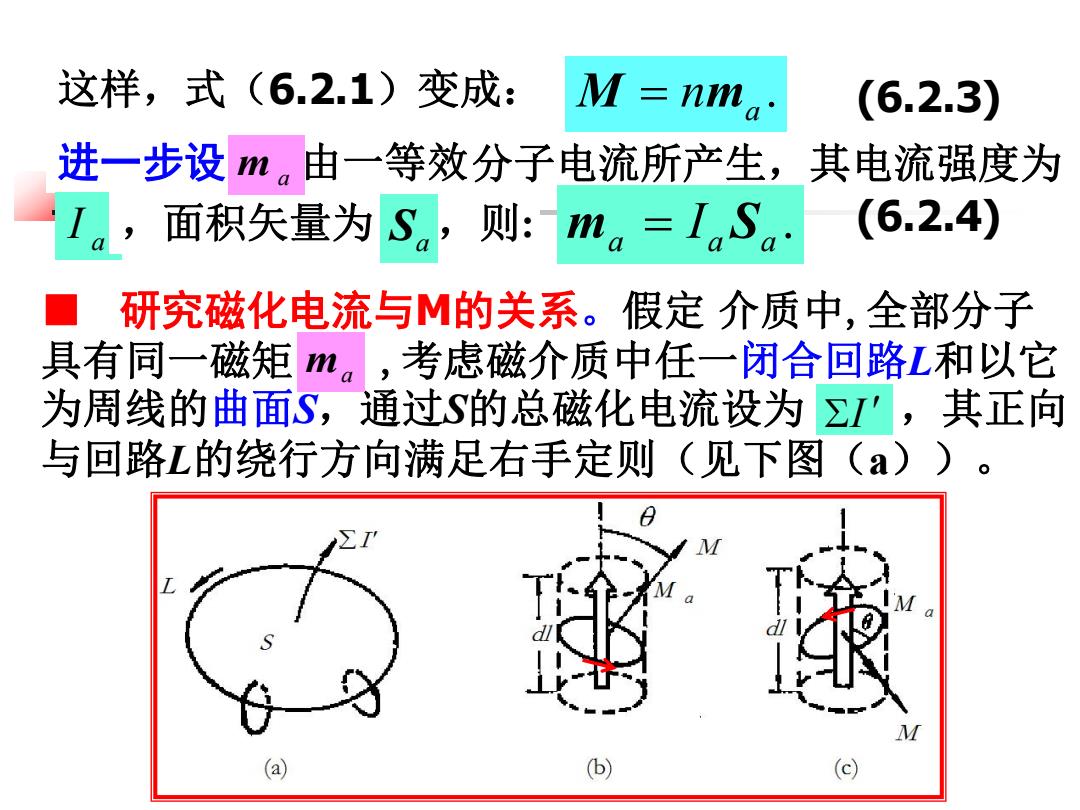
这样,式(6.2.1)变成: 进一步设 由一等效 . a M nm (6.2.3) 分子电流所产生,其电流强度为 a I ,面积矢量为 ,则: Sa . a a a m I S (6.2.4) ■ 研究磁化电流与M的关系。假定 介质中,全部分子 具有同一磁矩 ,考虑磁介质中任一闭合回路L和以它 为周线的曲面S,通过S的总磁化电流设为 ,其正向 与回路L的绕行方向满足右手定则(见下图(a))。 I ma m a

显然,只有那些从S内穿过并在S外闭合的分子电流才 对∑'有贡献;其它分子电流,或者来回穿过S,或者 根本不与S相交,对Σ'的净贡献为零。 考虑L上一段弧元,其方向沿回路绕行方向。设 在dl处磁化强度M与d的夹角为0。先分析0≤0≤π/2 的情况。不难看出,对'有贡献的分子的中心应位 于前页的图(b)所示的圆柱体中,大小为: △∑I'=IanS。cosθdl=nm ·d1=M·dl 当π/2<0≤π时(见前页图(c)),上式也成立, 所得磁化电流为负。M的环量为将上式沿L积分,得到 它与穿过S的总磁 化电流的关系: M.dL= (6.2.5) 穿乳
显然,只有那些从S内穿过并在S外闭合的分子电流才 对 有贡献;其它分子电流,或者来回穿过S,或者 根本不与S相交,对 的净贡献为零。 ■ 考虑L上一段弧元dl,其方向沿回路绕行方向。设 在dl处磁化强度M与dl的夹角为 。先分析 的情况。不难看出,对 有贡献的分子的中心应位 于前页的图(b)所示的圆柱体中,大小为: I I 0 /2 I cos a a a I I nS dl nm dl M dl 当 时(见前页图(c)),上式也成立, 所得磁化电流为负。M的环量为将上式沿L积分,得到 它与穿过S的总磁 /2 化电流的关系: . (6.2.5) L d I ' M L = 穿L

说明:这一关系不仅对介质内部的回路成立,而且对 跨过介质界面的回路也成立。如果介质均匀磁化,即 M=常量,则 M-M=M:fal=0 L L 即均匀磁化介质内,磁化电流为零。 研究磁化面电流与的关系。磁化电流不仅出现 在非均匀磁化介质中,还常以面电流形式存在于介质 表面。下面来分析磁化面电流和磁化强度之间的关系 考虑介质表面上任一面元,设其内侧磁化强度为 M;外侧为真空。取直角坐标系Oxyz,使y-z平面与所 考虑的面元相切,x轴指向面元外法线方向(如下页图 (a)
说明:这一关系不仅对介质内部的回路成立,而且对 跨过介质界面的回路也成立。如果介质均匀磁化,即 M=常量,则 0 L M dl M dl L 即均匀磁化介质内,磁化电流为零。 ■ 研究磁化面电流与M的关系。磁化电流不仅出现 在非均匀磁化介质中,还常以面电流形式存在于介质 表面。下面来分析磁化面电流和磁化强度之间的关系。 考虑介质表面上任一面元,设其内侧磁化强度为 M;外侧为真空。取直角坐标系Oxyz,使y-z平面与所 考虑的面元相切,x轴指向面元外法线方向(如下页图 (a))