
(6.3.5) 穿 这就是经过变形之后的磁介质中静磁场的安培环 路定理,它的右边不再出现磁化电流。后面,我们将 会看到,对于线性各向同性介质且具有一维对称性的 情况,可用式(6.3.5)安培环路定理简化求静磁场 的计算。 式(6.3.2)和式(6.3.5)涉及两个物理量B和 H,还必须通过引入B和H之间的关系才能完全确定静 磁场的具体形式。这说明,在引入辅助矢量H之后, 表面上回避了直接计算磁化电流的复杂性,但却带来 了分析B和H的关系的新问题。下面我们就来分析这一 关系,即介质的磁化规律
(6.3.5) ■ 这就是经过变形之后的磁介质中静磁场的安培环 路定理,它的右边不再出现磁化电流。后面,我们将 会看到,对于线性各向同性介质且具有一维对称性的 情况,可用式(6.3.5)安培环路定理简化求静磁场 的计算。 ■ 式(6.3.2)和式(6.3.5)涉及两个物理量B和 H,还必须通过引入B和H之间的关系才能完全确定静 磁场的具体形式。这说明,在引入辅助矢量H 之后, 表面上回避了直接计算磁化电流的复杂性,但却带来 了分析B和H的关系的新问题。下面我们就来分析这一 关系,即介质的磁化规律

§6.4 介质的磁化规律 介质按磁化规律的分类 介质的磁化规律,即M和B的关系, 是由实验 决定。由于历史的原因,人们常用M和H之间的关系 来表达介质的磁化规律。实验表明,对线性各向同性 磁介质: M= H. (6.4.1) 将上式代入式(6.3.4)求得磁介质的性能方程: B=4(H+M)=4,(1+Xm)H=WH (6.4.2) 式中: u=4(1+Xm)=4o4, (6.4.3) Xm称为磁化率,4称为磁导率。 在真空M=0,Xm=0, 4=4。称4为绝对磁导率,4三/4为相对磁导率
§6.4 介质的磁化规律 一 、介质按磁化规律的分类 介质的磁化规律,即M和B的关系,是由实验 决定。由于历史的原因,人们常用M和H之间的关系 来表达介质的磁化规律。实验表明,对线性各向同性 磁介质: . M m H (6.4.1) 将上式代入式(6.3.4)求得磁介质的性能方程: 0 0 B (H M) (1+ m )H=H (6.4.2) 式中: 0 0 (1 ) m r (6.4.3) 称为磁化率, 称为磁导率。在真空 , 。称 为绝对磁导率, 为相对磁导率。 m M 0 0, m 0 0 / r

磁介质按磁化规律不同可分为以下几类: (1)顺磁质和抗磁质 有的磁介质Xm>0,4>4o, 称为顺磁质;有的磁介 质Xm<0,μ<4,,称为抗磁质。这两种磁介质的磁 化率的绝对值都很小,前者约在104-105之间,后者 约在105-10-7之间(见表6.1),都属于弱磁性物质 。 ■实验发现一般抗磁质的磁化率不随温度变化而改变: 而一般顺磁质的磁化率与温度T成反比关系,遵从居里 定律: Xm (6.4.4) 式中C是居里常数,由实验确定。 ■对各向异性磁介质(例如晶体介质),M和H的方向 不一样,相应的磁化率和磁导率均为张量
(1) 顺磁质和抗磁质 有的磁介质 , ,称为顺磁质;有的磁介 质 , ,称为抗磁质。这两种磁介质的磁 化率的绝对值都很小,前者约在 之间,后者 约在 之间(见表6.1),都属于弱磁性物质。 ■ 实验发现一般抗磁质的磁化率不随温度变化而改变; 而一般顺磁质的磁化率与温度T成反比关系,遵从居里 定律: 式中C是居里常数,由实验确定。 ■ 对各向异性磁介质(例如晶体介质),M和H的方向 不一样,相应的磁化率和磁导率均为张量。 0 m 0 0 m 0 4 5 10 10 5 7 10 10 / , m C T (6.4.4) 磁介质按磁化规律不同可分为以下几类:
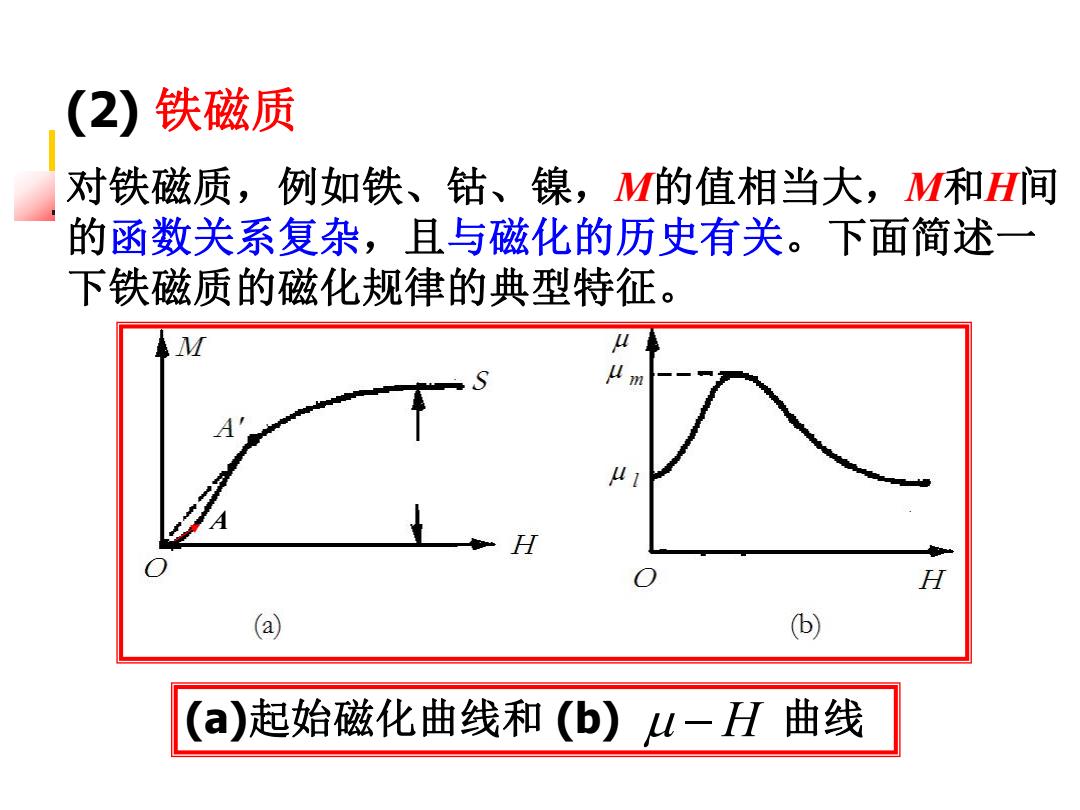
(2)铁磁质 对铁磁质,例如铁、钴、镍,M的值相当大,M和H间 的函数关系复杂,且与磁化的历史有关。下面简述一 下铁磁质的磁化规律的典型特征。 H (a) (b) (a)起始磁化曲线和(b)u-H曲线
(2) 铁磁质 对铁磁质,例如铁、钴、镍,M的值相当大,M和H间 的函数关系复杂,且与磁化的历史有关。下面简述一 下铁磁质的磁化规律的典型特征。 (a)起始磁化曲线和 (b) H 曲线 A

■闭合磁化曲线SRCSR'CS称为磁带回线。 ■按照矫顽力H。的大小,可把铁磁质划分为硬磁材料和 软磁材料两大类。前者矫顽力大,磁滞回线较宽(见 下图());后者矫顽力小,磁滞回线较窄(见下图 (b))。 MR M H (a) (b) 磁滞回线
■闭合磁化曲线SRCS‘R’C‘S称为磁滞回线。 ■按照矫顽力 的大小,可把铁磁质划分为硬磁材料和 软磁材料两大类。前者矫顽力大,磁滞回线较宽(见 下图(a));后者矫顽力小,磁滞回线较窄(见下图 (b))。 Hc 磁滞回线 Hc MR