
【例4.2-1】将下图所示方波信号展开为傅里叶级数。 f(t) E 2 E/ 解:按题意方波信号在一个周期内的解析式为 E 2 -h≤1<0 f0)= E-2 0≤1≤2 分求初德思时系:a.号f(号}com.+子〔}ex.ne,.d 57ksmapa+6aagl-o sinned =n7kcasna儿e+(cosnoW] 2p-2odas】 2E n为奇数 即: b. nπ 0 n为偶数 故得信号的傅里叶级数展开式为 f0=2E sine,1+sin3a/+2in50t+.+2 sinmo,.f+. 3 它只含有一、三、五、.等奇次谐波分量
【例 4.2-1】将下图所示方波信号展开为傅里叶级数。 f (t) 2 E 0 2 −T 2 T t 2 − E 解:按题意方波信号在一个周期内的解析式为 ( ) − − = 2 0 2 0 2 2 t T E T t E f t 分别求得傅里叶系数: cos 2 2 cos 2 2 2 0 0 0 2 0 + = − − T n T n tdt E T n tdt E T a ( sin ) (sin ) 0 n E 2 0 0 0 0 2 0 = − + = − T T n t n t T + = − − 2 0 0 0 2 0 sin 2 2 sin 2 2 T n T n tdt E T n tdt E T b ( ) ( ) 2 0 0 0 0 2 0 cos cos n E T T n t n t T = + − − ( ) n n E 2 2cos 2 = − 即: = 为偶数 为奇数 n n n E bn 0 2 故得信号的傅里叶级数展开式为 ( ) = + + ++ n t + n t t t E f t 0 0 0 0 sin 1 sin5 5 1 sin3 3 1 sin 2 它只含有一、三、五、.等奇次谐波分量
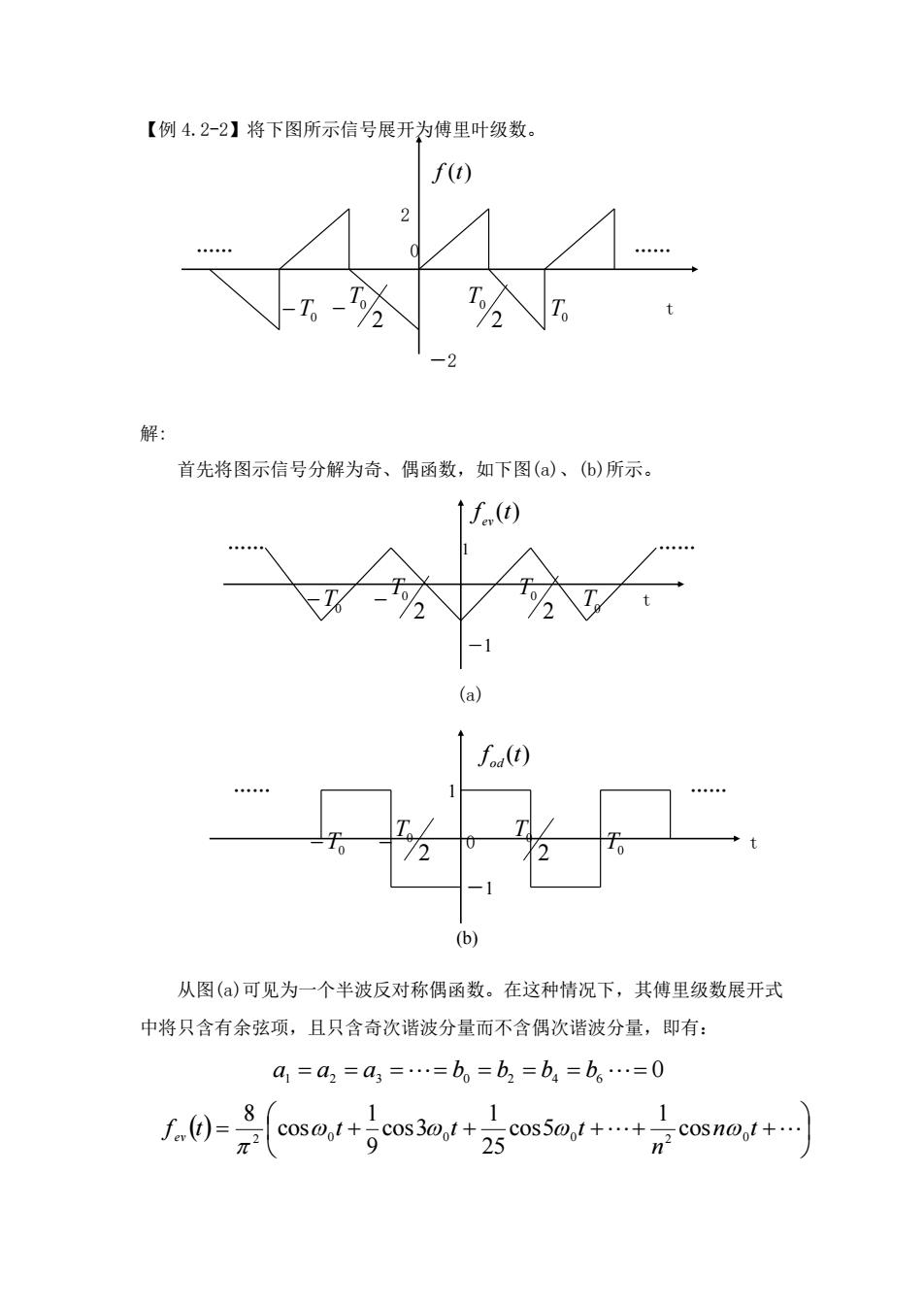
【例4.2-2】将下图所示信号展开为傅里叶级数。 f(t) 2 解: 首先将图示信号分解为奇、偶函数,如下图(a)、(b)所示。 f(+ (a) f(t) 2 0 (b) 从图()可见为一个半波反对称偶函数。在这种情况下,其傅里级数展开式 中将只含有余弦项,且只含奇次谐波分量而不含偶次谐波分量,即有: a1=a2=a3=.=b。=b2=b4=b。.=0 .0=cosa1+,+25os501+.++
【例 4.2-2】将下图所示信号展开为傅里叶级数。 f (t) 2 . 0 . −T0 2 − T0 2 T0 T0 t -2 解: 首先将图示信号分解为奇、偶函数,如下图(a)、(b)所示。 f (t) ev . 1 . −T0 2 − T0 2 T0 T0 t -1 (a) f (t) od . 1 . −T0 2 − T0 0 2 T0 T0 t -1 (b) 从图(a)可见为一个半波反对称偶函数。在这种情况下,其傅里级数展开式 中将只含有余弦项,且只含奇次谐波分量而不含偶次谐波分量,即有: a1 = a2 = a3 == b0 = b2 = b4 = b6 = 0 ( ) = + + ++ n t + n f t t t t ev 2 0 0 0 2 0 cos 1 cos5 25 1 cos3 9 1 cos 8

从图(b)可见为一个半波反对称奇函数。在这种情况下,其傅里级数展开式 中将只含有正弦项,且只含奇次谐波分量而不含偶次谐波分量,即有: a=42=a4=.=b=b=b2=b3.=0 0-气mog+兮nau+5na++方ina+. 。1 ∴f(t)=fn(t)+foa(t) 、8 1 .1 元2 cos cos 4 1 + ,1 π sino+sin3s.sin+
从图(b) 可见为一个半波反对称奇函数。在这种情况下,其傅里级数展开式 中将只含有正弦项,且只含奇次谐波分量而不含偶次谐波分量,即有: a0 = a2 = a4 == b0 = b1 = b2 = b3 = 0 ( ) = + + ++ n t + n f t t t t o d 0 0 0 0 sin 1 sin5 5 1 sin3 3 1 sin 4 f (t) f (t) f (t) = ev + od = + + ++ n t + n t t t 2 0 0 0 2 0 cos 1 cos5 25 1 cos3 9 1 cos 8 + + + ++ n t + n t t t 0 0 0 0 sin 1 sin5 5 1 sin3 3 1 sin 4