
然而,将会看到,如果一个信号是带限的(即它的傅 里叶变换在某一有限频带以外均为零),并且它的样 本取得足够密的话(样本数>ω。,相对于信号中的最 高频率而言),那么这些样本值就能唯一地用来表征 这一信号,并且能从这些样本中把信号完全恢复出 来。这一结果就是采样定理。 0
然而,将会看到,如果一个信号是带限的(即它的傅 里叶变换在某一有限频带以外均为零),并且它的样 本取得足够密的话(样本数>> ,相对于信号中的最 高频率而言),那么这些样本值就能唯一地用来表征 这一信号,并且能从这些样本中把信号完全恢复出 来。这一结果就是采样定理。 0 ω ωc ωc

7.1用信号样本表示连续时间信号:采样定理 ?怎样得到一个连续时间 信号x()的样本值 {x(nT),n=0,±1,±2,…} 答案:冲激串采样。 第7章采样 9
第7章 采样 9 7.1 用信号样本表示连续时间信号:采样定理 ?怎样得到一个连续时间 信号x(t)的样本值 { ( ), 0, 1, 2, } x nT n = ±± 答案:冲激串采样
7.1.1冲激串采样 为了建立采样定理,我们需要一种方法来表示一个连 续时间信号在均匀间隔上的采样,即通过用一个周期 冲激串去乘待采样的连续时间 p 信号x()。这一方法称为冲激串 采样。该周期冲激串p()称为采 样函数,周期称为采样周期, ×他 而p()的基波频率⊙,=2π/T 称为采样频率。 ÷在时域中有 xp(④=p()x(t) 其中 p()=∑6t-nT) n=-00 图7,2冲藏串采样
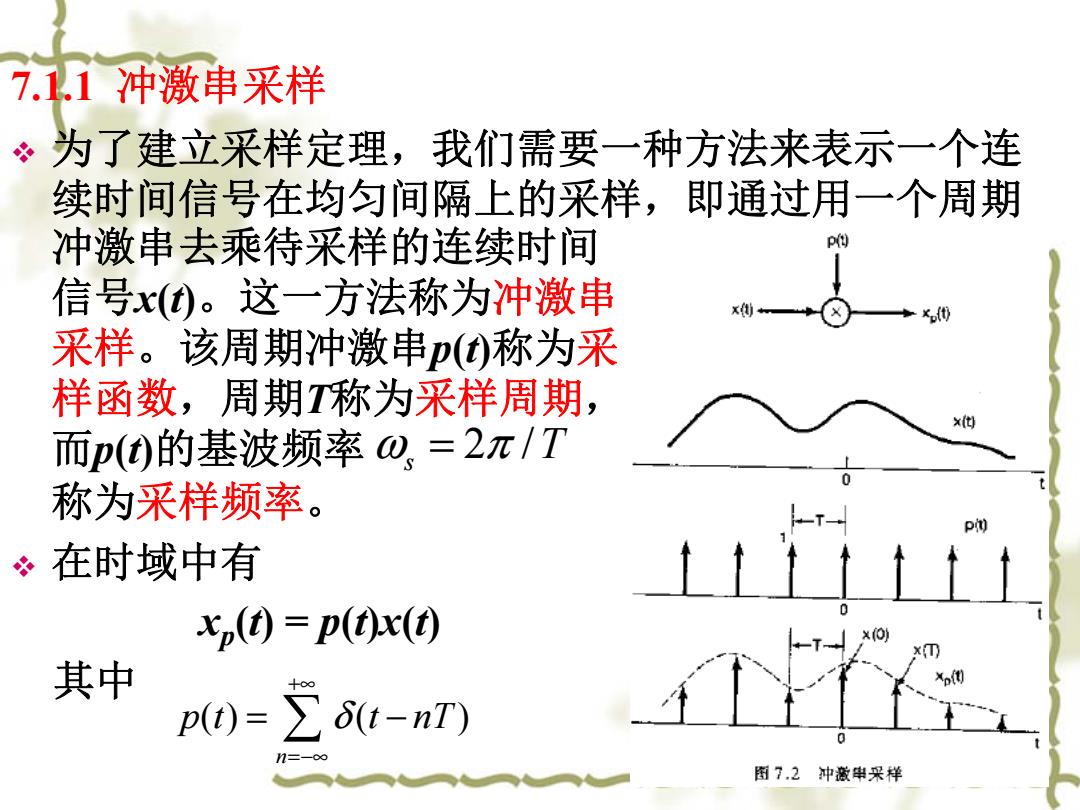
7.1.1 冲激串采样 为了建立采样定理,我们需要一种方法来表示一个连 续时间信号在均匀间隔上的采样,即通过用一个周期 冲激串去乘待采样的连续时间 信号x (t)。这一方法称为冲激串 采样。该周期冲激串p (t)称为采 样函数,周期T称为采样周期, 而p (t)的基波频率 称为采样频率。 在时域中有 xp (t) = p(t)x(t) 其中 2 / ω π s = T () ( ) n p t t nT δ +∞ =−∞ = −

由在1.4.2节曾讨论过的单位冲激函数的性质有: x(t)8(t-t)=x(to)8(t-to) 于是有 ●● x,(t)=∑x()t-nT)=∑x(nT)6t-nT) 1=-co n=-00 可见x,)本身就是一个冲激串,其冲激的幅度等于x() 在以T为间隔处的样本值。 由傅里叶变换的相乘性质知道: X,U@=2元[XUo)*PUw]
由在1.4.2节曾讨论过的单位冲激函数的性质有: 于是有 可见xp ( t)本身就是一个冲激串,其冲激的幅度等于 x ( t) 在以 T为间隔处的样本值。 由傅里叶变换的相乘性质知道: 00 0 xt t t xt t t () ( ) ( ) ( ) δ δ −= − () () ( ) ( ) ( ) p n n x t x t t nT x nT t nT δ δ +∞ +∞ =−∞ =−∞ = −= − 1 ( ) [ ( ) ( )] 2 X p jω ωω X j P j π = ∗
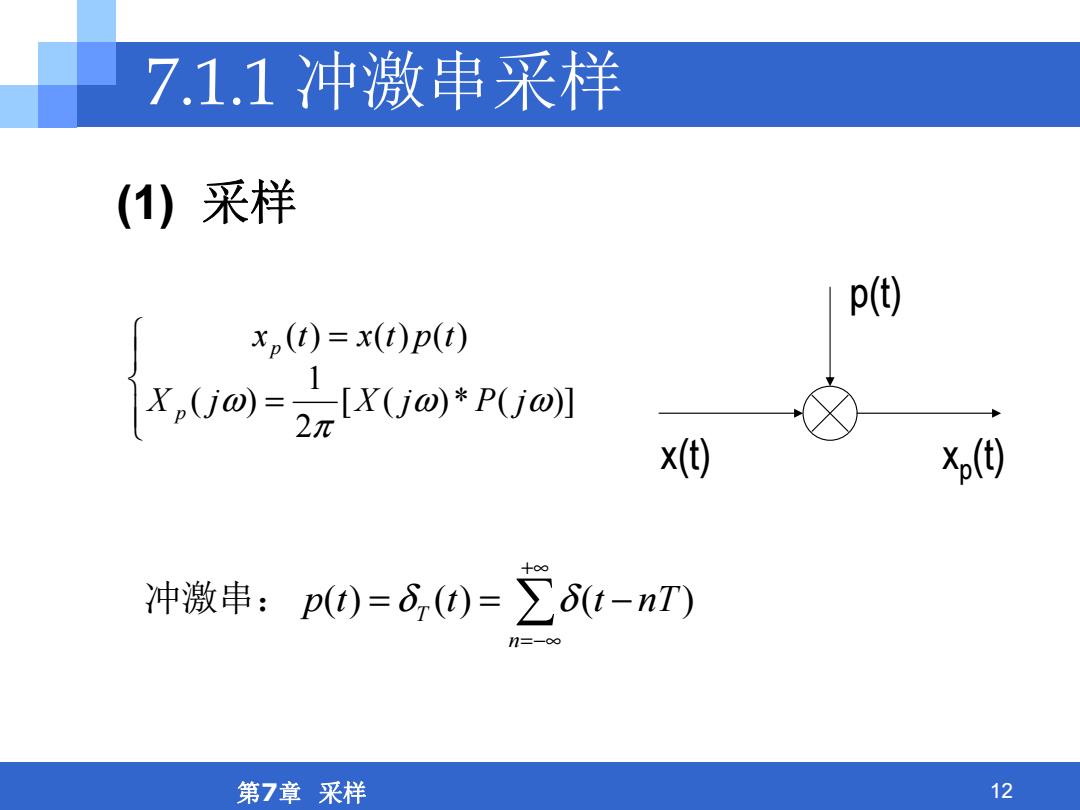
7.1.1冲激串采样 (1)采样 p(t) x,(t)=x(t)p(t) x,Uo=2zXUoPUo1 x(t) 仞 冲激串:p(0=6,()=∑6t-nT) 1=-o 第7章采样 12
第7章 采样 12 7.1.1 冲激串采样 = = )](*)([ 21 )( )()()( ωω π ω jPjXjX tptxtx p p x(t) p(t) xp (t) +∞ =−∞ −== n 冲激串: T δδ nTtttp )()()( (1) 采样