
即△x,=X,一x。偏差又叫做“残差”。实验中真值得不到,因此误差也无法知道, 而测量的偏差可以准确知道,实验误差分析中要经常计算这种偏差,用偏差来描述 测量结果的精确程度。 1.1.3相对误差 绝对误差与真值之比的百分数叫做相对误差。用E表示: E、4 -×100% N 由于真值无法知道,所以计算相对误差时常用N代替。在这种情况下,N可能是 公认值,或高一级精密仪器的测量值,或测量值的平均值。相对误差用来表示测量 的相对精确度,相对误差用百分数表示,保留两位有效数字。 1.1.4系统误差与随机误差 根据误差的性质和产生的原因,可分为系统误差和随机误差 系统误差是指在一定条件下多次测量的结果总是向一个方向偏离,其数值一定或按 一定规律变化。系统误差的特征是具有一定的规律性。系统误差的来源具有以下几 个方面:(1)仪器误差。它是由于仪器本身的缺陷或没有按规定条件使用仪器而造 成的误差:(2)理论误差。它是由于测量所依据的理论公式本身的近似性,或实验 条件不能达到理论公式所规定的要求,或测量方法等所带来的误差:(3)观测误差。 它是由于观测者本人生理或心理特点造成的误差,例如,用“落球法“测量重力加速度, 由于空气阻力的影响,多次测量的结果总是偏小,这是测量方法不完善造成的误差: 用停表测量运动物体通过某一段路程所需要的时间,若停表走时太快,即使测量多 次,测量的时间【总是偏大为一个固定的数值,这是仪器不准确造成的误差:在测 量过程中,若环境温度升高或降低,使测量值按一定规律变化,是由于环境因素变 化引起的误差。 在任何一项实验工作和具体测量中,必须要想尽一切办法,最大限度的消除或 减、小一切可能存在的系统误差,或者对测量结果进行修正。发现系统误差需要改 变实验条件和实验方法,反复进行对比,系统误差的消除或减小是比较复杂的一个 问题,没有固定不变的方法,要具体问题具体分析各个击破。产生系统误差的原因 可能不止一个,一般应找出影响的主要因素,有针对性地消除或减小系统误差。以 下介绍几种常用的方法。 检定修正法:指将仪器、量具送计量部门检验取得修正值,以便对某一物理量 测量后进行修正的一种方法。 10
10 即 x x x i i 。偏差又叫做“残差”。实验中真值得不到,因此误差也无法知道, 而测量的偏差可以准确知道,实验误差分析中要经常计算这种偏差,用偏差来描述 测量结果的精确程度。 1.1.3 相对误差 绝对误差与真值之比的百分数叫做相对误差。用E表示: 100% 0 N N E 由于真值无法知道,所以计算相对误差时常用N代替 N0 。在这种情况下,N可能是 公认值,或高一级精密仪器的测量值,或测量值的平均值。相对误差用来表示测量 的相对精确度,相对误差用百分数表示,保留两位有效数字。 1.1.4 系统误差与随机误差 根据误差的性质和产生的原因,可分为系统误差和随机误差。 系统误差 是指在一定条件下多次测量的结果总是向一个方向偏离,其数值一定或按 一定规律变化。系统误差的特征是具有一定的规律性。系统误差的来源具有以下几 个方面:(1)仪器误差。它是由于仪器本身的缺陷或没有按规定条件使用仪器而造 成的误差;(2)理论误差。它是由于测量所依据的理论公式本身的近似性,或实验 条件不能达到理论公式所规定的要求,或测量方法等所带来的误差;(3)观测误差。 它是由于观测者本人生理或心理特点造成的误差。例如,用“落球法”测量重力加速度, 由于空气阻力的影响,多次测量的结果总是偏小,这是测量方法不完善造成的误差; 用停表测量运动物体通过某一段路程所需要的时间,若停表走时太快,即使测量多 次,测量的时间 t 总是偏大为一个固定的数值,这是仪器不准确造成的误差;在测 量过程中,若环境温度升高或降低,使测量值按一定规律变化,是由于环境因素变 化引起的误差。 在任何一项实验工作和具体测量中,必须要想尽一切办法,最大限度的消除或 减、小一切可能存在的系统误差,或者对测量结果进行修正。发现系统误差需要改 变实验条件和实验方法,反复进行对比,系统误差的消除或减小是比较复杂的一个 问题,没有固定不变的方法,要具体问题具体分析各个击破。产生系统误差的原因 可能不止一个,一般应找出影响的主要因素,有针对性地消除或减小系统误差。以 下介绍几种常用的方法。 检定修正法:指将仪器、量具送计量部门检验取得修正值,以便对某一物理量 测量后进行修正的一种方法

替代法:指测量装置测定待测量后,在测量条件不变的情况下,用一个已知标准量 替换被测量来减小系统误差的一种方法。如消除天平的两臂不等对待测量的影响可 用此办法。 异号法:指对实验时在两次测量中出现符号相反的误差,采取平均值后消除的 一种方法。例如在外界磁场作用下,仪表读数会产生一个附加误差,若将仪表转动 180°再进行一次测量,外磁场将对读数产生相反的影响,引起负的附加误差。两次测 量结果平均,正负误差可以抵消,从中可以减小系统误差。 随机误差在实际测量条件下,多次测量同一量时,误差的绝对值符号的变化,时大 时小、时正时负,以不可预定方式变化着的误差叫做随机误差,有时也叫偶然误差。 当测量次数很多时,随机误差就显示出明显的规律性。实践和理论都已证明,随机 误差服从一定的统计规律(正态分布),其特点是:绝对值小的误差出现的概率比 绝对值大的误差出现的概率大(单峰性):绝对值相等的正负误差出现的概率相同 (对称性):绝对值很大的误差出现的概率趋于零(有界性):误差的算术平均值 随着测量次数的增加而趋于零(抵偿性)。因此,增加测量次数可以减小随机误差, 但不能完全消除。 引起随机误差的原因也很多。仪器精密度和观察者感官灵敏度有关。如仪器显 示数值的估计读数位偏大和偏小:仪器调节平衡时,平衡点确定不准:测量环境扰 动变化以及其他不能预测不能控制的因素,如空间电磁场的干扰,电源电压波动引 起测量的变化等。 由于测量者过失,如实验方法不合理,用错仪器,操作不当,诗错数值或记错 数据等引起的误差,是一种人为的过失误差,不属于测量误差,只要测量者采用严 肃认真的态度,过失误差是可以避免的。 实验中,精密度高是指随机误差小,而数据很集中:准确度高是指系统误差小, 测量的平均值偏离真值小:精确度高是指测量的精密度和准确度都高。数据集中而 且偏离真值小,即随机误差和系统误差都小。 1.1.5测量的精密度、准确度和精确度 测量的精密度、准确度和精确度都是评价测量结果的术语,但目前使用时其涵 义并不尽一致,以下介绍较为普遍采用的意见。 测量精密度表示在同样测量条件下,对同一物理量进行多次测量,所得结果彼 此间相互接近的程度,即测量结果的重复性、测量数据的弥散程度,因而测量精密 度是测量偶然误差的反映。测量精密度高,偶然误差小,但系统误差的大小不明确 测量准确度表示测量结果与真值接近的程度,因而它是系统误差的反映。测量准确 度高,则测量数据的算术平均值偏离真值较小,测量的系统误差小,但数据较分散, 偶然误差的大小不确定。测量精确度则是对测量的偶然误差及系统误差的综合评定。 精确度高,测量数据较集中在真值附近,测量的偶然误差及系统误差都比较小。 11
11 替代法:指测量装置测定待测量后,在测量条件不变的情况下,用一个已知标准量 替换被测量来减小系统误差的一种方法。如消除天平的两臂不等对待测量的影响可 用此办法。 异号法:指对实验时在两次测量中出现符号相反的误差,采取平均值后消除的 一种方法。例如在外界磁场作用下,仪表读数会产生一个附加误差,若将仪表转动 180°再进行一次测量,外磁场将对读数产生相反的影响,引起负的附加误差。两次测 量结果平均,正负误差可以抵消,从中可以减小系统误差。 随机误差 在实际测量条件下,多次测量同一量时,误差的绝对值符号的变化,时大 时小、时正时负,以不可预定方式变化着的误差叫做随机误差,有时也叫偶然误差。 当测量次数很多时,随机误差就显示出明显的规律性。实践和理论都已证明,随机 误差服从一定的统计规律(正态分布),其特点是:绝对值小的误差出现的概率比 绝对值大的误差出现的概率大(单峰性);绝对值相等的正负误差出现的概率相同 (对称性);绝对值很大的误差出现的概率趋于零(有界性);误差的算术平均值 随着测量次数的增加而趋于零(抵偿性)。因此,增加测量次数可以减小随机误差, 但不能完全消除。 引起随机误差的原因也很多。仪器精密度和观察者感官灵敏度有关。如仪器显 示数值的估计读数位偏大和偏小;仪器调节平衡时,平衡点确定不准;测量环境扰 动变化以及其他不能预测不能控制的因素,如空间电磁场的干扰,电源电压波动引 起测量的变化等。 由于测量者过失,如实验方法不合理,用错仪器,操作不当,读错数值或记错 数据等引起的误差,是一种人为的过失误差,不属于测量误差,只要测量者采用严 肃认真的态度,过失误差是可以避免的。 实验中,精密度高是指随机误差小,而数据很集中;准确度高是指系统误差小, 测量的平均值偏离真值小;精确度高是指测量的精密度和准确度都高。数据集中而 且偏离真值小,即随机误差和系统误差都小。 1.1.5 测量的精密度、准确度和精确度 测量的精密度、准确度和精确度都是评价测量结果的术语,但目前使用时其涵 义并不尽一致,以下介绍较为普遍采用的意见。 测量精密度表示在同样测量条件下,对同一物理量进行多次测量,所得结果彼 此间相互接近的程度,即测量结果的重复性、测量数据的弥散程度,因而测量精密 度是测量偶然误差的反映。测量精密度高,偶然误差小,但系统误差的大小不明确。 测量准确度表示测量结果与真值接近的程度,因而它是系统误差的反映。测量准确 度高,则测量数据的算术平均值偏离真值较小,测量的系统误差小,但数据较分散, 偶然误差的大小不确定。测量精确度则是对测量的偶然误差及系统误差的综合评定。 精确度高,测量数据较集中在真值附近,测量的偶然误差及系统误差都比较小

1.1.6随机误差的估算 对某一测量进行多次重复测量,其测量结果服从一定的统计规律,也就是正态 分布(或高斯分布)。我们用描述高斯分布的两个参量(x和σ)来估算随机误差。 设在一组测量值中,n次测量的值分别为:,,x 1.算术平均值 根据最小二乘法原理证明,多次测量的算术平均值 (1) ni 是待测量真值x。的最佳估计值。称x为近似真实值,以后我们将用x来表示多次 测量的近似真实值 2.标准偏差 误差理论证明,平均值的标准偏差 S,=0,= (贝塞尔公式) (2) n-1 其意义表示某次测量值的随机误差在一σ,~+σ,之间的概率为683%。 1.1.7算术平均值的标准偏差 当测量次数n有限,其算术平均值的标准偏差为 ,- (3) 其意义是测量平均值的随机误差在-0,~+σ,之间的概率为68.3%。或者说,待测 量的真值在(-0:(+G:k范围内的概率为683%.因此x0反映了平均 值接近真值的程度。 1.1.8标准偏差σ
12 1.1.6 随机误差的估算 对某一测量进行多次重复测量,其测量结果服从一定的统计规律,也就是正态 分布(或高斯分布)。我们用描述高斯分布的两个参量(x 和 σ)来估算随机误差。 设在一组测量值中,n 次测量的值分别为:x1, x2 ,…xn 1.算术平均值 根据最小二乘法原理证明,多次测量的算术平均值 n i i x n x 1 1 (1) 是待测量真值 0 x 的最佳估计值。称 x 为近似真实值,以后我们将用 x 来表示多次 测量的近似真实值。 2.标准偏差 误差理论证明,平均值的标准偏差 1 1 2 n x x S n i i x x (贝塞尔公式) (2) 其意义表示某次测量值的随机误差在 x ~ x 之间的概率为 68.3%。 1.1.7 算术平均值的标准偏差 当测量次数 n 有限,其算术平均值的标准偏差为 1 1 2 n n x x n n i i x x (3) 其意义是测量平均值的随机误差在 x ~ x 之间的概率为 68.3%。或者说,待测 量的真值在 x x ~ x x x 范围内的概率为 68.3%。因此 x σ 反映了平均 值接近真值的程度。 1.1.8 标准偏差 x

标准偏差σ,小表示测量值密集,即测量的精密度高:标准偏差。,大表示测量值分 散,即测量的精密度低。估计随机误差还有用算术平均误差、2σ,、36。等其它 方法来表示的。 1.1.9异常数据的剔除 剔除测量列中异常数据的标准有几种,有3。,准则、肖维准则、格拉布斯 准则等。 1.3。准则 统计理论表明,测量值的偏差超过3。,的概率已小于1%。因此,可以认为 偏差超过3。,的测量值是其他因素或过失造成的,为异常数据,应当剔除。剔除的 方法是将多次测量所得的一系列数据,算出各测量值的偏差△x和标准偏差。,,把 其中最大的△y与3o,比较,若△y>3σ,,则认为第j个测量值是异常数据, 舍去不计。剔除:后,对余下的各测量值重新计算偏差和标准偏差,并继续审查, 直到各个偏差均小于30,为止。 2.肖维准则 假定对一物理量重复测量了n次,其中某一数据在这n次测量中出现的几率不 到半次,即小于 1 ,则可以肯定这个数据的出现是不合理的,应当予以剔除, 2n 根据肖维准则,应用随机误差的统计理论可以证明,在标准误差为。的测量列中, 若某一个测量值的偏差等于或大于误差的极限值K。,则此值应当剔出。不同测量次 数的误差极限值K。列于下表。 表1肖维系数表 Ka n K。 4 153o 10 196o 16 2.160 5 1.65 11 2.00o 2.18 6 1.73o 12 2.040 18 2.20o > 1.79g 13 2.07o 19 2.220 8 1.86o 14 2.10c 0 2.240 9 1.92 15 2.13c 21 2.39
13 标准偏差 x 小表示测量值密集,即测量的精密度高;标准偏差 x 大表示测量值分 散,即测量的精密度低。估计随机误差还有用算术平均误差、2 x 、3 x 等其它 方法来表示的。 1.1.9 异常数据的剔除 剔除测量列中异常数据的标准有几种,有 3 x 准则、肖维准则、格拉布斯 准则等。 1.3 x 准则 统计理论表明,测量值的偏差超过 3 x 的概率已小于 1%。因此,可以认为 偏差超过 3 x 的测量值是其他因素或过失造成的,为异常数据,应当剔除。剔除的 方法是将多次测量所得的一系列数据,算出各测量值的偏差 Δxi 和标准偏差 x ,把 其中最大的 Δxj 与 3 x 比较,若 Δxj >3 x ,则认为第 j 个测量值是异常数据, 舍去不计。剔除 xj 后,对余下的各测量值重新计算偏差和标准偏差,并继续审查, 直到各个偏差均小于 3 x 为止。 2.肖维准则 假定对一物理量重复测量了 n 次,其中某一数据在这 n 次测量中出现的几率不 到半次,即小于 2n 1 ,则可以肯定这个数据的出现是不合理的,应当予以剔除。 根据肖维准则,应用随机误差的统计理论可以证明,在标准误差为 σ 的测量列中, 若某一个测量值的偏差等于或大于误差的极限值 Kσ ,则此值应当剔出。不同测量次 数的误差极限值 Kσ 列于下表。 表 1 肖维系数表 n Kσ n Kσ n Kσ 4 1.53σ 10 1.96σ 16 2.16σ 5 1.65σ 11 2.00σ 17 2.18σ 6 1.73σ 12 2.04σ 18 2.20σ 7 1.79σ 13 2.07σ 19 2.22σ 8 1.86σ 14 2.10σ 20 2.24σ 9 1.92σ 15 2.13σ 21 2.39σ
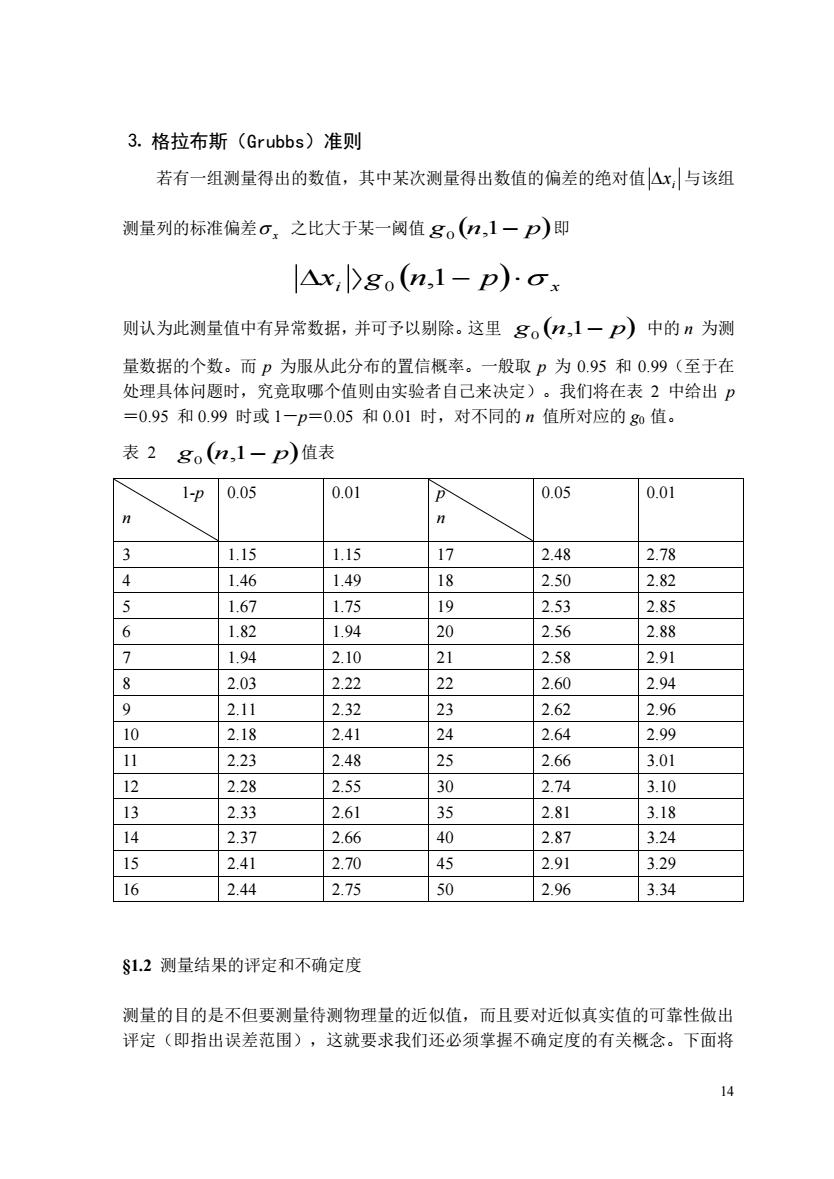
3.格拉布斯(Grubbs)准则 若有一组测量得出的数值,其中某次测量得出数值的偏差的绝对值△x,与该组 测量列的标准偏差σ,之比大于某一阀值g。(n,1一p)即 △x,>go(n,1-p)ox 则认为此测量值中有异常数据,并可予以剔除。这里go(n,1一P)中的n为测 量数据的个数。而p为服从此分布的置信概率。一般取p为0.95和0.99(至于在 处理具体问题时,究竟取哪个值则由实验者自己来决定)。我们将在表2中给出p =0.95和0.99时或1一p=0.05和0.01时,对不同的n值所对应的0值。 表2gon,1-p)值表 1-p0.05 0.01 D 0.05 0.01 3 1.15 1.15 17 2.48 2.78 4 1.46 1.49 18 2.50 2.82 167 175 19 2.53 2.85 6 1.82 1.94 20 2.56 2.88 7 1.94 2.10 21 2.58 2.91 8 203 222 22 260 2.94 9 2.11 2.32 23 2.62 2.96 10 2.18 241 24 2.64 2.99 11 2.23 2.48 35 2.66 3.01 12 228 255 30 274 3.10 13 2.33 2.61 35 2.81 3.18 14 2.37 2.66 40 2.87 3.24 15 241 2.70 45 291 329 16 2.44 2.75 50 2.96 3.34 S12测量结果的评定和不确定度 测量的目的是不但要测量待测物理量的近似值,而且要对近似真实值的可靠性做出 评定(即指出误差范围),这就要求我们还必须掌握不确定度的有关概念。下面将 14
14 ⒊ 格拉布斯(Grubbs)准则 若有一组测量得出的数值,其中某次测量得出数值的偏差的绝对值 i x 与该组 测量列的标准偏差 x 之比大于某一阈值 g n,1 p 0 即 xi g n p x ,1 0 则认为此测量值中有异常数据,并可予以剔除。这里 g n,1 p 0 中的 n 为测 量数据的个数。而 p 为服从此分布的置信概率。一般取 p 为 0.95 和 0.99(至于在 处理具体问题时,究竟取哪个值则由实验者自己来决定)。我们将在表 2 中给出 p =0.95 和 0.99 时或 1-p=0.05 和 0.01 时,对不同的 n 值所对应的 g0 值。 表 2 g n,1 p 0 值表 1-p n 0.05 0.01 p n 0.05 0.01 3 1.15 1.15 17 2.48 2.78 4 1.46 1.49 18 2.50 2.82 5 1.67 1.75 19 2.53 2.85 6 1.82 1.94 20 2.56 2.88 7 1.94 2.10 21 2.58 2.91 8 2.03 2.22 22 2.60 2.94 9 2.11 2.32 23 2.62 2.96 10 2.18 2.41 24 2.64 2.99 11 2.23 2.48 25 2.66 3.01 12 2.28 2.55 30 2.74 3.10 13 2.33 2.61 35 2.81 3.18 14 2.37 2.66 40 2.87 3.24 15 2.41 2.70 45 2.91 3.29 16 2.44 2.75 50 2.96 3.34 §1.2 测量结果的评定和不确定度 测量的目的是不但要测量待测物理量的近似值,而且要对近似真实值的可靠性做出 评定(即指出误差范围),这就要求我们还必须掌握不确定度的有关概念。下面将