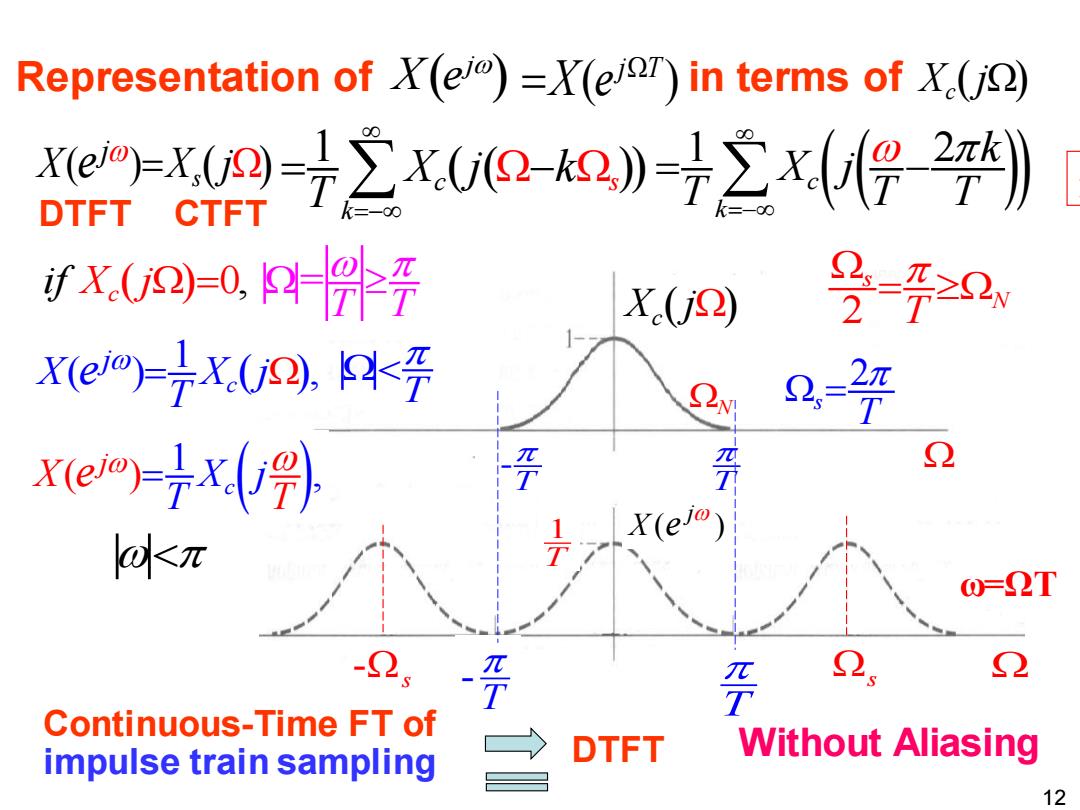
Representation of X(ei)=Y(eisr)in terms of X(j) Xem=XU0=7立xUQo》=72x(2T) DTFT CTFT fx.U9)-0,4+号 X.(2) 牙>2 X(ej)-FX.(jD).Kf 2 2π x(e)-fxj9) X(ej@) okπ 0=2T -2g 妥 Continuous-Time FT of impulse train sampling DTFT Without Aliasing 12
12 ( ) ( ) s j X e X j = Representation of in terms of ( ) j X e X j c ( ) ( ( )) 1 c s k X j k T =− = − ( ( )) 1 2 c k k X j T T T =− = − s Continuous-Time FT of impulse train sampling - T X j c ( ) T - T ( ) j X e 1 T - s i Xc ( ) 0, = T f j T = ( ) 1 ( ) , c j X X j T e = T DTFT ( ) 1 ( ) , c j X j T X T e = DTFT Without Aliasing ( ) j T X e = 2 s T = 是 T 2 s N T = N ω=ΩT CTFT
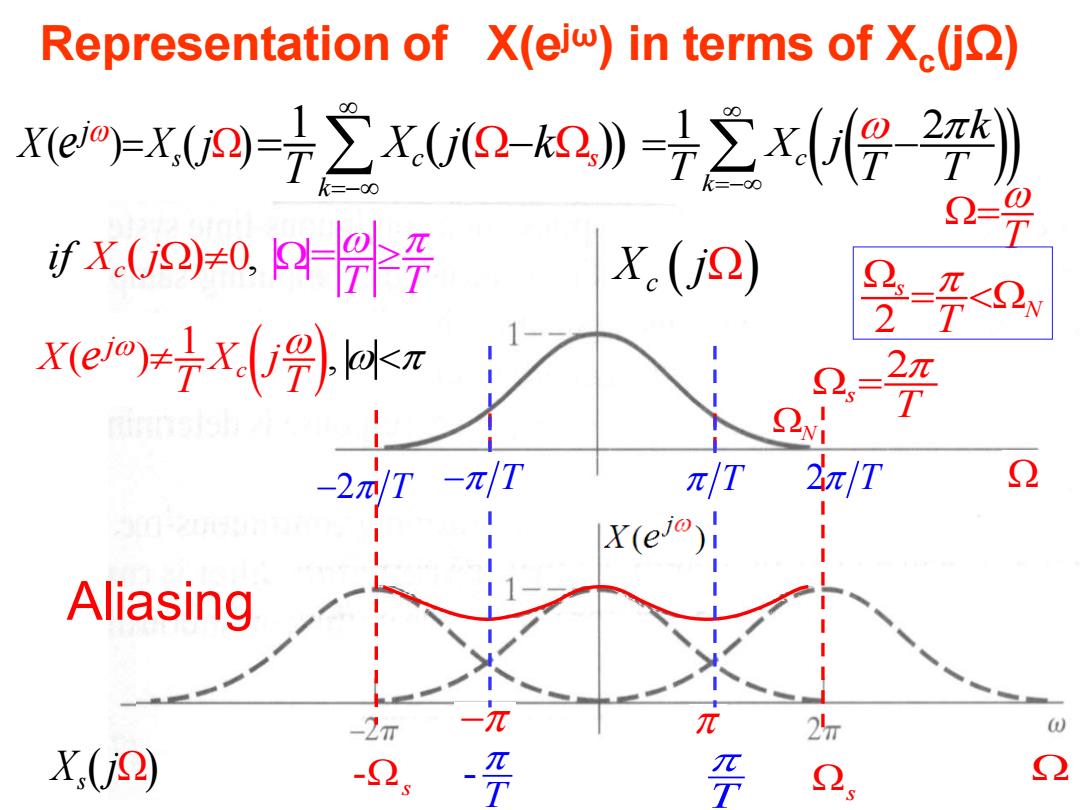
Representation of X(ei)in terms of X(jQ) KexU9-72xUQ-2》-7x(号2*) = fXU904+晋 Y.(j2) 2 xem≠7x(体a 2π T -2例 -π/1 π/T 2π/T 2 Aliasing -2m π 2 ⊙ X,(2) 牙 2 2
14 − Representation of X(ejω) in terms of Xc (jΩ) − −2 T 2 T Aliasing ( ( )) 1 2 c k k X j T T T =− = − T = ( ( )) 1 c s k X j k T =− = − ( ) 1 ( ) , c j X X j T T e i Xc ( ) 0, = T f j T − T T X j c ( ) 2 s T =2 s N T = N s T - T - s ( ) ( ) s j X e X j = ( ) X j s

Nyquist Sampling Theorem Let x(t)be a bandlimited signal with X.(j2-0,for12p2v·If2,-2平≥22v, then X()is uniquely determined by its samples x[n=x.(nT),n=0,±l,±2,... The frequency is commonly referred as the Nyquist frequency. The frequency 20 is called the Nyquist rate, which is the minimum sampling rate (frequency) without Aliasing. 16
• Let be a bandlimited signal with . If , then is uniquely determined by its samples ( ), 0, 1, 2, . x n x nT n = = c 2 s N 2 T = X t c ( ) 16 Nyquist Sampling Theorem •The frequency is commonly referred as the Nyquist frequency. N •The frequency is called the 2N Nyquist rate, X t c ( ) ( ) 0, X j for c = N which is the minimum sampling rate (frequency) without Aliasing
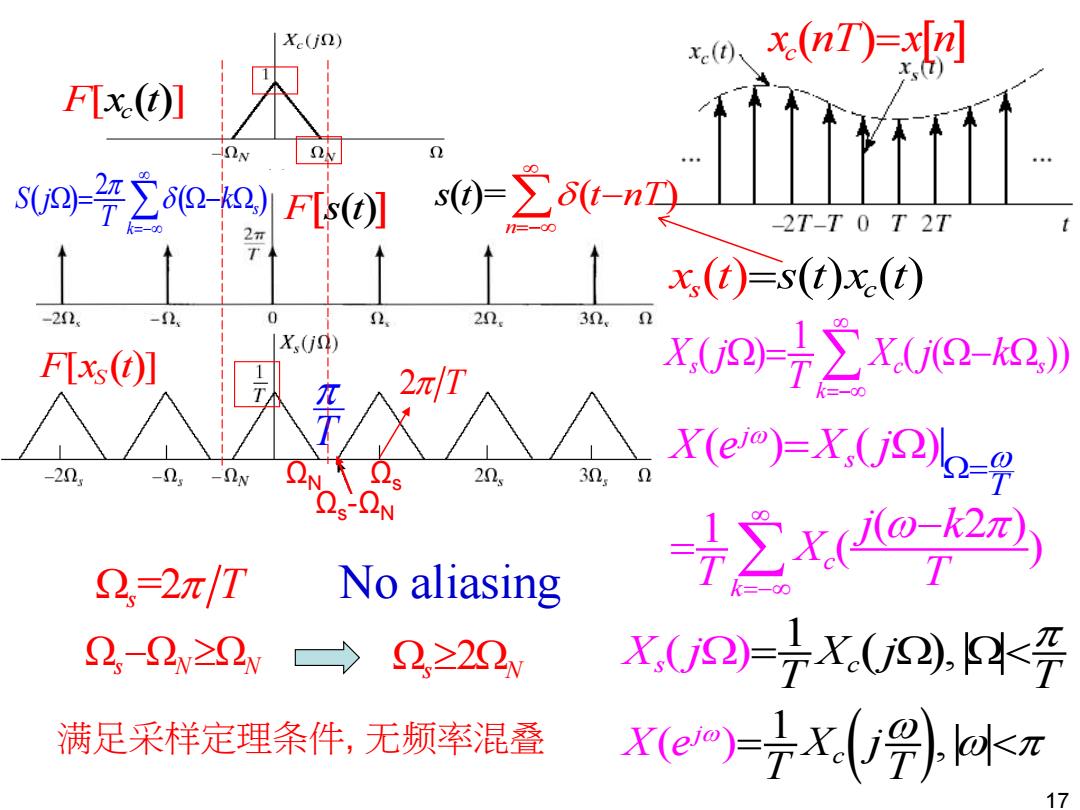
X.(jn) x.0 x.(nT)=xn (O UQ42平∑0-2)F[s(0】 s0-2ot-n70 -2T-T 0 T 2T 2元 x,(t)=s(t)x.(E) -21 -2 0 2 2n. 3.2 X,0) FIxs(t)] 2xT X(U2-=+∑XU2-2》 20 -且y -2w 30 Ω X(eJ0)-X.(jD)-g OS ON 2,=2π/T No aliasing =72X(o2 2,-2v22v→ 2,≥20w X,(j2)=X.(i2),4<开 满足采样定理条件,无频率混叠 Xem=7x(9》)kn
17 No aliasing 1 ( ) ( ( )) s c s k X j X j k T =− = − ( ) ( )| j s T X e X j = = ( ) ( ) 2 s k S j k T =− = − 1 ( 2 ) ( ) c k j k X T T =− − = ( ) 1 ( ) , s Xc j T X j T − s N N = T 2 T F[ ] x t c ( ) ( )= ( ) n s t t nT =− − xs (t)=s t (t x) c ( ) Fs t( ) F x t [ ] S ( ) x nT x n c ( )= s =2 T s N 2 满足采样定理条件, 无频率混叠 Ωs -ΩN ΩN Ωs ( ) 1 ( ) , j Xc T T X e j =
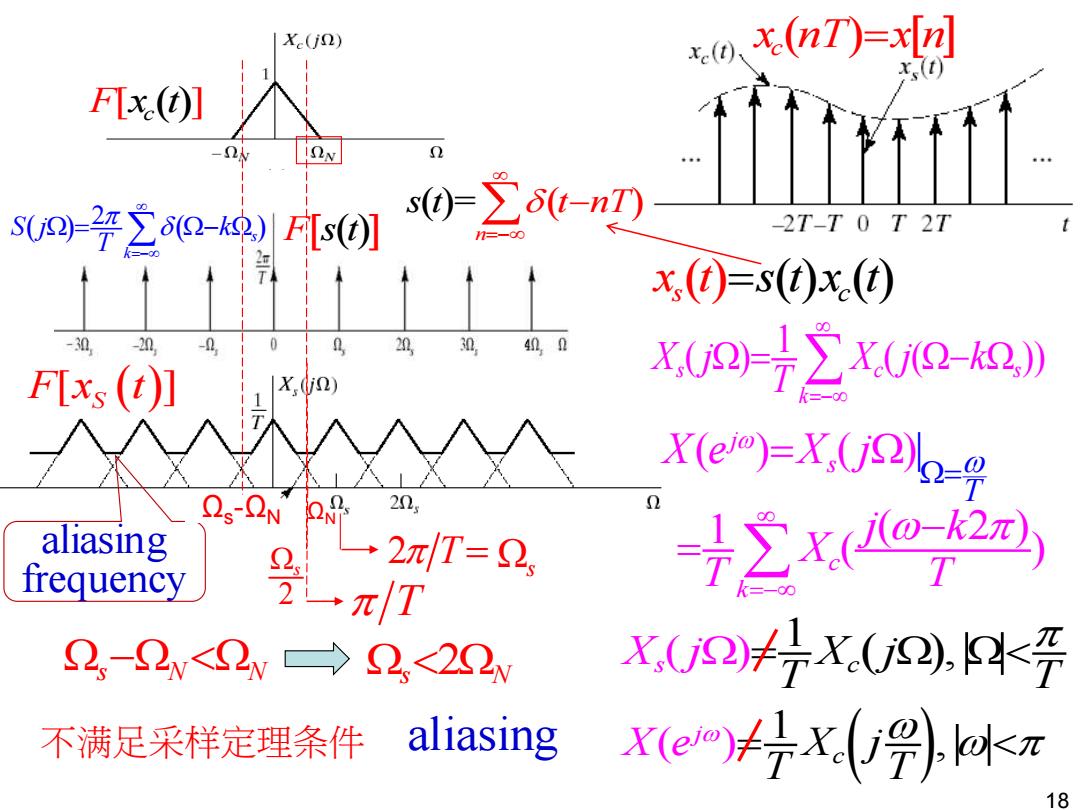
X(j2) .0、x(nI)=x[刀 Fx.(O] ● SU22平∑6Q-k)FLs(0 s)-∑6t-nT) -2T-T 0 T 2T x()=()x.() -2n -0 20, 30 FIxs (t)] X(272X.0Q-2》 X(ej)=X.(j)-g Os-ON 20g aliasing 一2π/T=2 frequency =72K02 2,-2v<2v→2,<22v Xj2/行X.U2,非4< 不满足采样定理条件 aliasing X(emf7x别,元 78
( ) 1 ( ) , s Xc j T X j T = 18 2 s T 2 T 1 ( ) ( ( )) s c s k X j X j k T =− = − ( ) ( ) 2 s k S j k T =− = − 1 ( 2 ) ( ) c k j k X T T =− − = aliasing F[ ] x t c( ) ( )= ( ) n s t t nT =− − xs ( t ) =s t (t x) c( ) F s t( ) F x t [ ] S ( ) x nT x n c( )= − s N N = s s N 2 不满足采样定理条件 ( ) ( )| j s T X e X j = = aliasing frequency Ω s - Ω N ( ) 1 ( ) , j Xc T T X e j = Ω N