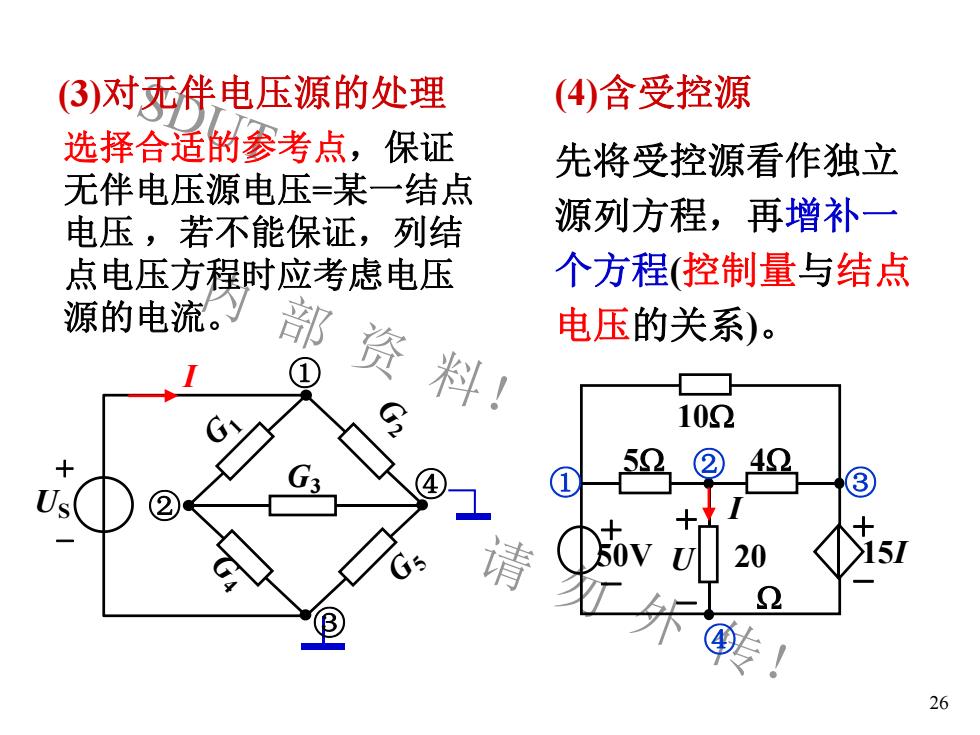
(4)含受控源(3)对无伴电压源的处理选择合适的参考点,保证先将受控源看作独立无伴电压源电压-某一结点源列方程,再增补一电压,若不能保证,列结个方程(控制量与结点点电压方程时应考虑电压源的电流。部资料!电压的关系)。1S102491G3314115150V20百外A26
SDUT 内 部 资 料! 请 勿 外 传! 26 (4)含受控源 50V 10 20 - + 4 + - 15I 5 U - + I ① ② ③ ④ 先将受控源看作独立 源列方程,再增补一 个方程(控制量与结点 电压的关系)。 (3)对无伴电压源的处理 选择合适的参考点,保证 无伴电压源电压=某一结点 电压 ,若不能保证,列结 点电压方程时应考虑电压 源的电流。 G2 G1 G G 5 4 + -US G3 ① ② ③ ④ I
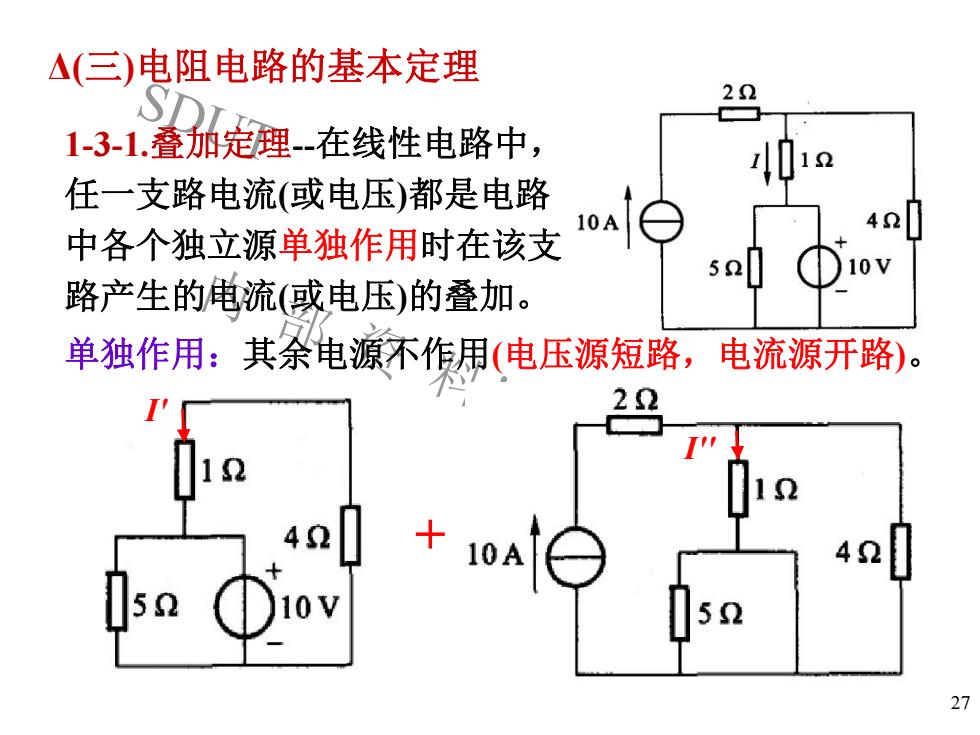
A(三)电阻电路的基本定理221-3-1.叠加定理--在线性电路中,S任一支路电流(或电压)都是电路10A中各个独立源单独作用时在该支10V59路产生的电流(或电压)的叠加。单独作用:其余电源不作用(电压源短路,电流源开路)22104.210A5210V5227
SDUT 内 部 资 料! 请 勿 外 传! 27 Δ(三)电阻电路的基本定理 I' I'' 单独作用:其余电源不作用(电压源短路,电流源开路)。 1-3-1.叠加定理-在线性电路中, 任一支路电流(或电压)都是电路 中各个独立源单独作用时在该支 路产生的电流(或电压)的叠加。 +
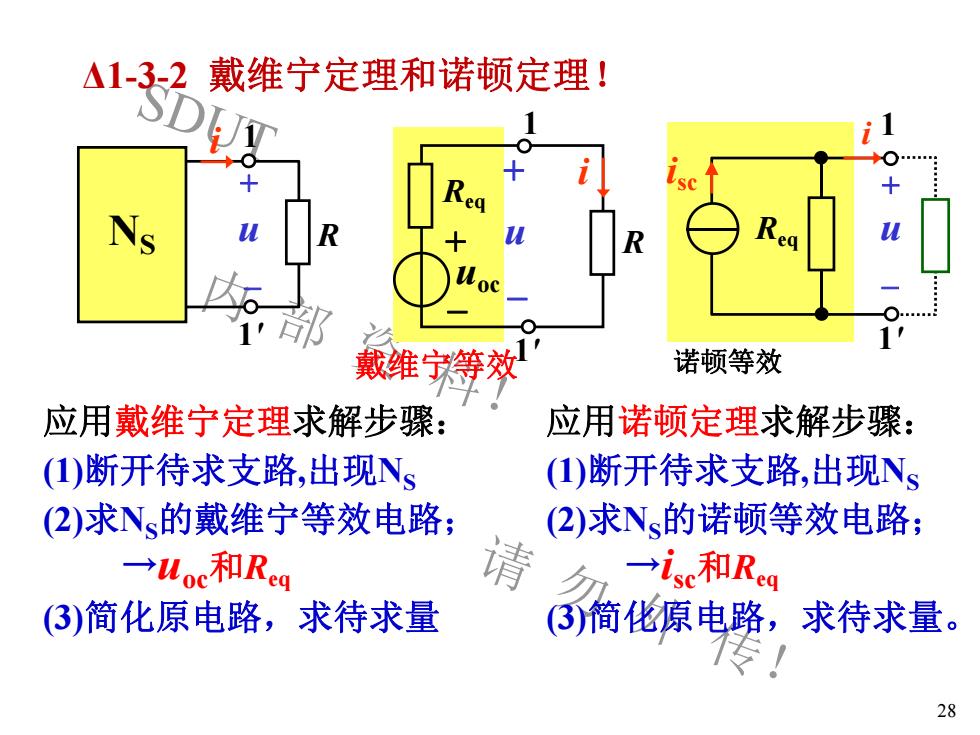
戴维宁定理和诺顿定理!A1-3-2SD1O十+'sc+ReqNsRequR人uRWoc6诺顿等效戴维宁等效应用戴维宁定理求解步骤:应用诺顿定理求解步骤:(1)断开待求支路,出现N。(1)断开待求支路,出现Ns(2)求Ns的戴维宁等效电路:(2)求Ns的诺顿等效电路:请→isc和Req→Uoc和Req(3)简化原电路,(3)简化原电路,求待求量求待求量。传28
SDUT 内 部 资 料! 请 勿 外 传! Δ1-3-2 戴维宁定理和诺顿定理! 28 i NS R + -u 1 1' + -Req i uoc R + u - 1 1' 应用戴维宁定理求解步骤: (1)断开待求支路,出现NS (2)求NS的戴维宁等效电路; →uoc和Req (3)简化原电路,求待求量 戴维宁等效 + - 1 1' Req i u isc 诺顿等效 应用诺顿定理求解步骤: (1)断开待求支路,出现NS (2)求NS的诺顿等效电路; →isc和Req (3)简化原电路,求待求量
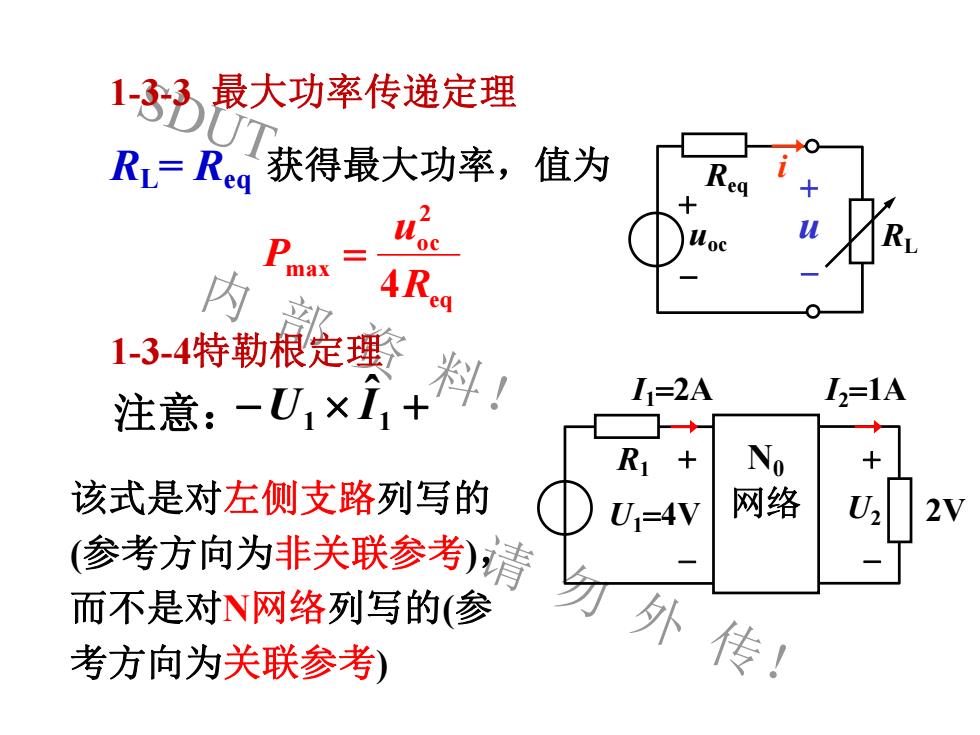
1-3-3最大功率传递定理获得最大功率,值为RL= ReqReqXRyWoc00max4R内eq1-3-4特勒根定理料Ii=2AI=1A注意:-U,×I +NoR1 ++该式是对左侧支路列写的网络U22VUi=4V分外传!而不是对N网络列写的(参考方向为关联参考
SDUT 内 部 资 料! 请 勿 外 传! + - Req uoc i + -u RL 获得最大功率,值为 4 eq 2 oc max R u P = 1-3-3 最大功率传递定理 RL= Req 注意:- 1 1 + ˆ U I 该式是对左侧支路列写的 (参考方向为非关联参考), 而不是对N网络列写的(参 考方向为关联参考) N0 网络 + - U1=4V + - R1 I1=2A I2=1A U2 2V 1-3-4特勒根定理

注意:特勒根定理和互易定理适用的条件不同特勒根定理任何时刻,对于两个具有n个结点和b条支路的集总电路,当它们具有相同的图,但由内容不同的支路构成,在支路电流和电压取关联参考2h方向下,满足:动ukin=0Ukik= 0,>,居“料!k=互易定理内容:对一个仅含线性电阻的且只有一个激励的电路,在保持电路将独立源置零后电路拓扑结构不变的条件下,激励和响应互换位置后,响应勿外传!与激励的比值保持不变30
SDUT 内 部 资 料! 请 勿 外 传! 30 互易定理内容:对一个仅含线性电阻的且只有一个 激励的电路,在保持电路将独立源置零后电路拓扑 结构不变的条件下,激励和响应互换位置后,响应 与激励的比值保持不变。 ∑ b k=1 uk i ˆ k = 0,∑ b k=1 uk i ˆ k = 0 特勒根定理:任何时刻,对于两个具有n个结点和b 条支路的集总电路,当它们具有相同的图,但由内 容不同的支路构成,在支路电流和电压取关联参考 方向下,满足: 注意:特勒根定理和互易定理适用的条件不同