(2)对称电路的等效电阻2例:S求RATRRRbR对称电路OFaoC、d等电位ORR资料!Rab= RddRRRR32RRRRbRRRRR2'RR1-RRRRYRRRRO,1'a(e")16(e)
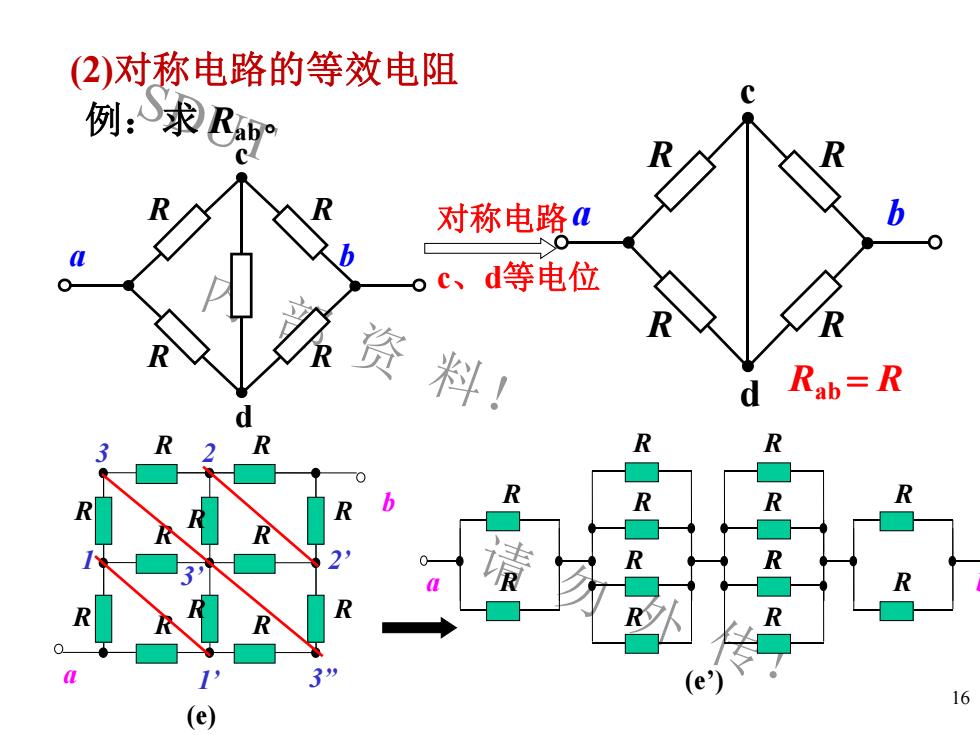
SDUT 内 部 资 料! 请 勿 外 传! 对称电路 c、d等电位 (2)对称电路的等效电阻 16 c a b R R R R d c a b R R R R d Rab = R 例:求 Rab。 a b (e) R R R R R R R R R R R R 1 1’ 2 2’ 3 3’ 3” a (e’) R R b R R R R R R R R R R
(3)电桥不平衡的等效电阻----Y←→ △的等效变换RiR2RR2+RR+RRR12 =R3R3RR, + R,R+ RRR23=3003RR部资料!10RR, + R,R3+ RRR31=R2R31R23R12 R310330Ri= R12 + R23 + Rs11三电阻相等R23 R12口R请R场Ru+Rrs+Rs13RR = 3Ry3R外RsRas!RR23R3= -R12 + R23+ R31d83R
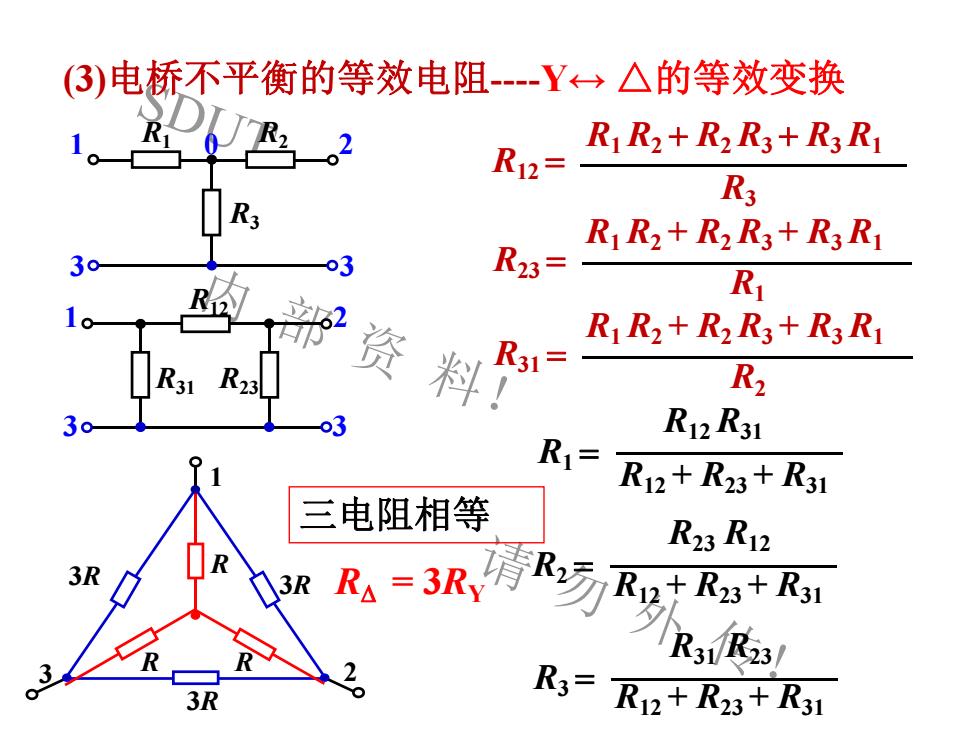
SDUT 内 部 资 料! 请 勿 外 传! R12 = R3 R1R2 + R2R3 + R3R1 R23 = R1 R1R2 + R2R3 + R3R1 R31 = R2 R1R2 + R2R3 + R3R1 R R 1 3 2 3R R 3R 3R R1 = R12R31 R12 + R23 + R31 R2 = R23 R12 R12 + R23 + R31 R3 = R31 R23 R12 + R23 + R31 三电阻相等 R = 3RY (3)电桥不平衡的等效电阻-Y↔ △的等效变换 1 0 2 3 3 R3 R1 R2 R31 R12 R23 1 2 3 3
4.含有受控源电路的等效电阻u①除(独立)源;R.eqi②端口外加电压源u,产生电流i;③列出电压u与电流的关系式,求uli或ilu。6i1 +h部二6162.iii米除源+X10V3232uO.请勿外传!18
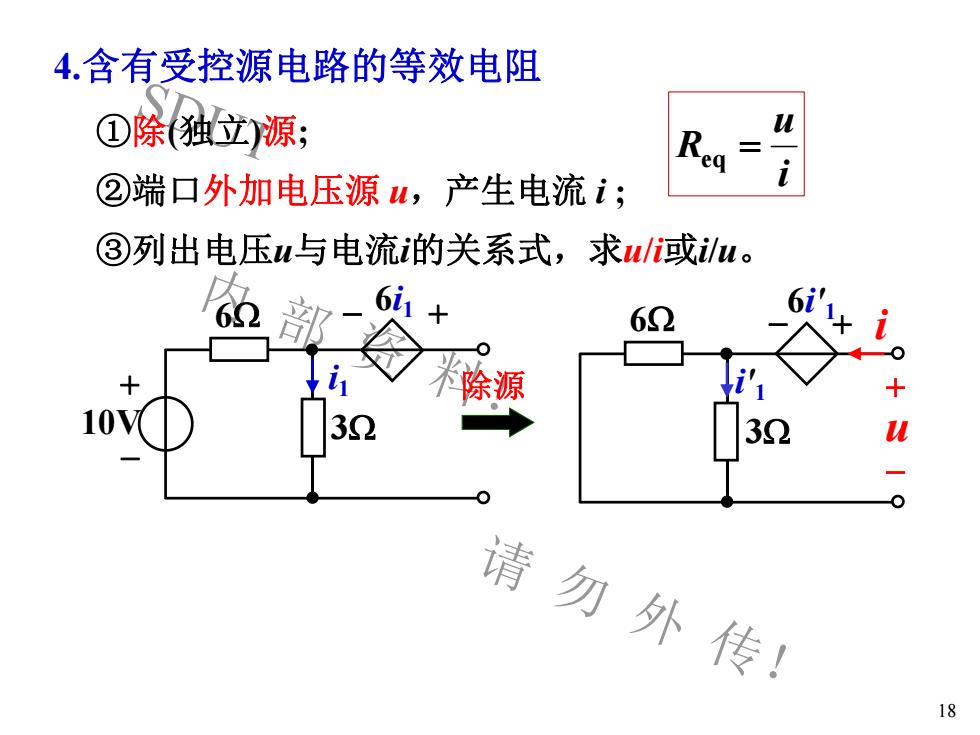
SDUT 内 部 资 料! 请 勿 外 传! 18 ①除(独立)源; ②端口外加电压源 u,产生电流 i ; ③列出电压u与电流i的关系式,求u/i或i/u。 4.含有受控源电路的等效电阻 + - 10V 6 - + 6i1 i1 3 i + -u 6 - + 6i′ 1 i′ 1 3 除源 i u Req =
(二)电阻电路的一般分析方法等效电源法A1-2-101usi011.理想电源的等效变换nZususk(1)串联uus2Sk=102usius2料usn等效电路n02(2)并联 i,=Zk=101tisiLSn= is1 -is2 +...isn2吕注意参考方向!119
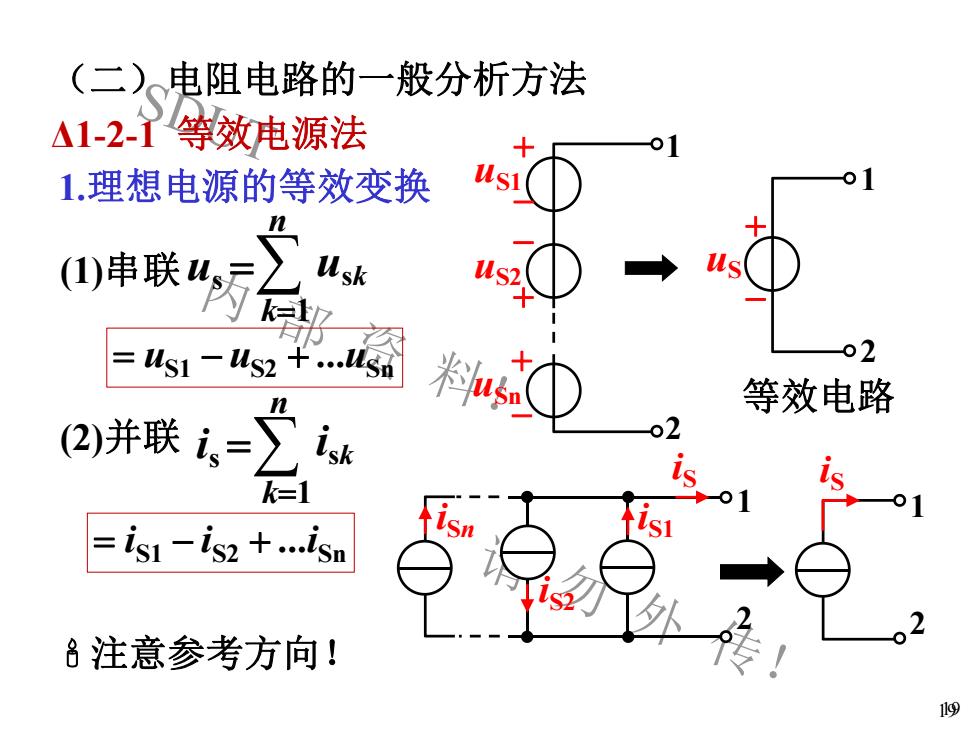
SDUT 内 部 资 料! 请 勿 外 传! 19 (二)电阻电路的一般分析方法 Δ1-2-1 等效电源法 19 1.理想电源的等效变换 1 2 us =∑ k=1 n usk 等效电路 注意参考方向! n is =∑ k=1 isk iS 1 2 iS1 iS2 iSn 1 2 iS (1)串联 (2)并联 1 2 + uS1 - - uS2 + + uSn - S1 S2 Sn = u - u + .u S1 S2 Sn = i - i + .i + uS -
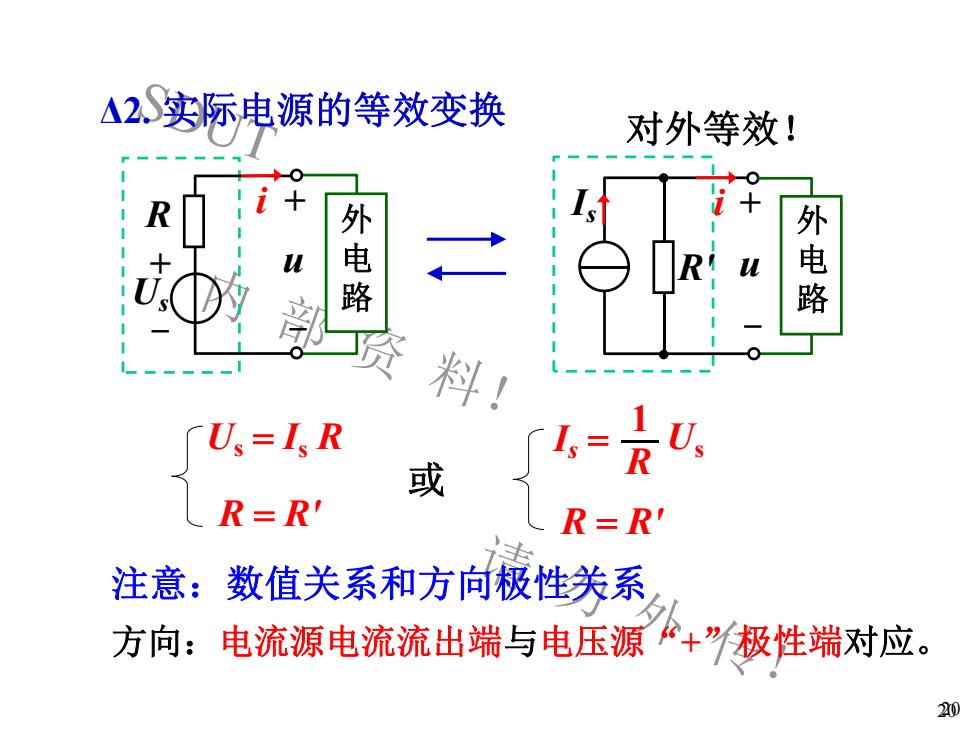
A2.S实际电源的等效变换对外等效!十+R外电路外电路uE资料!I,=U,U, =I, RR或R=R'R=R'持注意:数值关系和方向极性关系方向:原“+”极性端对应。电流源电流流出端与电压源20
SDUT 内 部 资 料! 请 勿 外 传! 20 对外等效! + -Us + -u R 外 电 路 i Is + - R′ u i 外 电 路 或 = I Us s R R = R′ R Is = 1 Us R = R′ 注意:数值关系和方向极性关系 方向:电流源电流流出端与电压源“+”极性端对应。 Δ2. 实际电源的等效变换