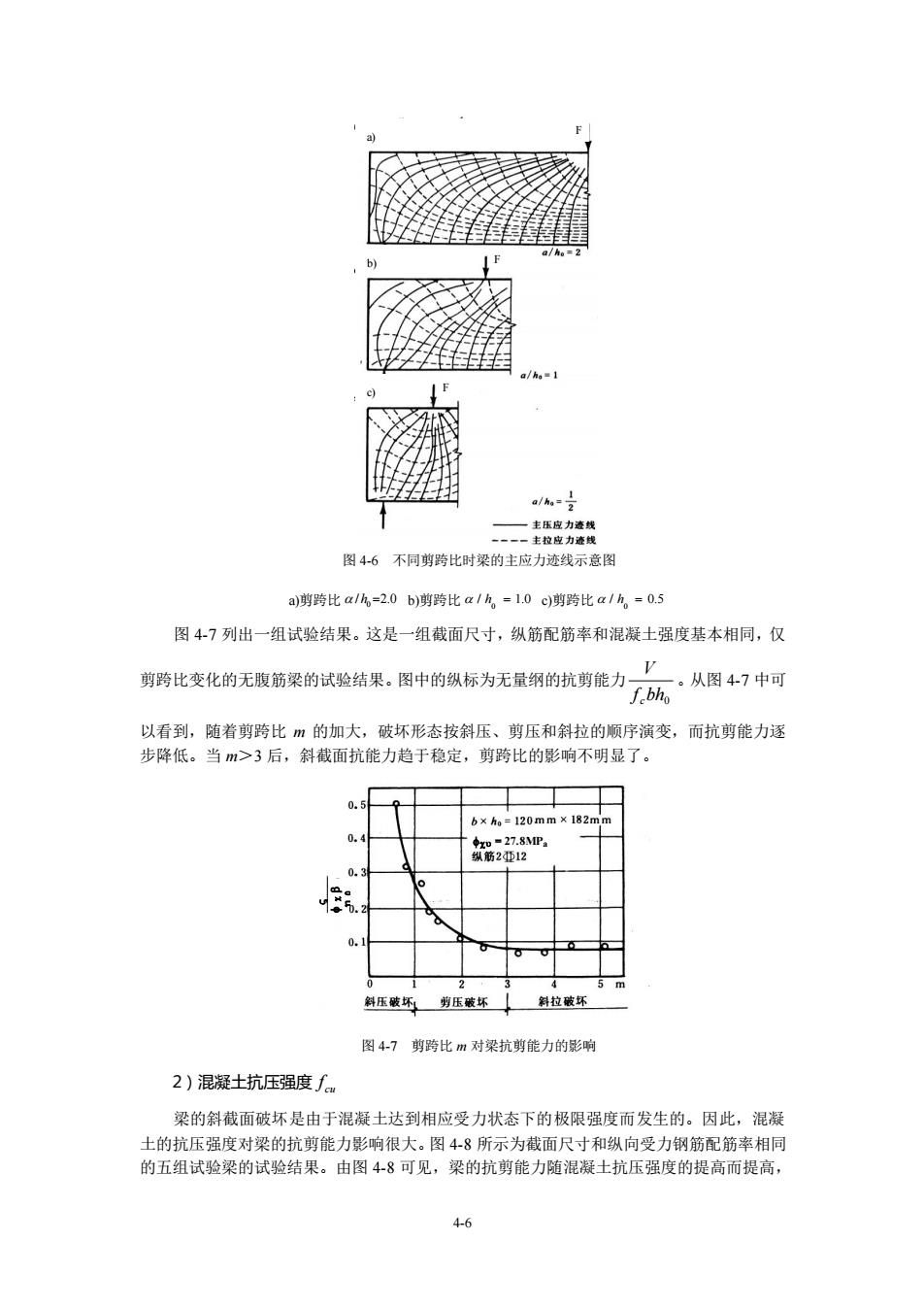
图46不同剪比时梁的主应力迹线示意图 a)蹲跨比a/%-20b)剪跨比a/%,-1.0c剪跨比a/%-0.5 图47列出一组试验结果。这是一组截面尺寸,纵筋配筋率和混凝土强度基本相同,仅 V 剪跨比变化的无腹筋梁的试验结果。图中的纵标为无量纲的抗剪能力 。从图47中可 以看到,随者剪跨比m的加大,破坏形态按斜压、剪压和斜拉的顺序演变,而抗剪能力逐 步降低。当m>3后,斜截面抗能力趋于稳定,剪跨比的影响不明显了。 b×h。=120 2 压乐剪压坏斜拉破坏 图4-7剪跨比m对梁抗剪能力的影响 2)混凝土抗压强度∫ 梁的斜截面破坏是由于混凝土达到相应受力状态下的极限强度而发生的。因此,混凝 土的抗压强度对梁的抗剪能力影响很大。图48所示为截面尺寸和纵向受力钢筋配筋率相同 的五组试验梁的试验结果。由图48可见,梁的抗剪能力随混凝土抗压强度的提高而提高, 4-6
4-6 图 4-6 不同剪跨比时梁的主应力迹线示意图 a)剪跨比 0 / 2.0 h = b)剪跨比 0 / 1.0 h = c)剪跨比 0 / 0.5 h = 图 4-7 列出一组试验结果。这是一组截面尺寸,纵筋配筋率和混凝土强度基本相同,仅 剪跨比变化的无腹筋梁的试验结果。图中的纵标为无量纲的抗剪能力 bh0 f V c 。从图 4-7 中可 以看到,随着剪跨比 m 的加大,破坏形态按斜压、剪压和斜拉的顺序演变,而抗剪能力逐 步降低。当 m>3 后,斜截面抗能力趋于稳定,剪跨比的影响不明显了。 图 4-7 剪跨比 m 对梁抗剪能力的影响 2)混凝土抗压强度 cu f 梁的斜截面破坏是由于混凝土达到相应受力状态下的极限强度而发生的。因此,混凝 土的抗压强度对梁的抗剪能力影响很大。图 4-8 所示为截面尺寸和纵向受力钢筋配筋率相同 的五组试验梁的试验结果。由图 4-8 可见,梁的抗剪能力随混凝土抗压强度的提高而提高, a) b) c) = 27.8MPa F F F
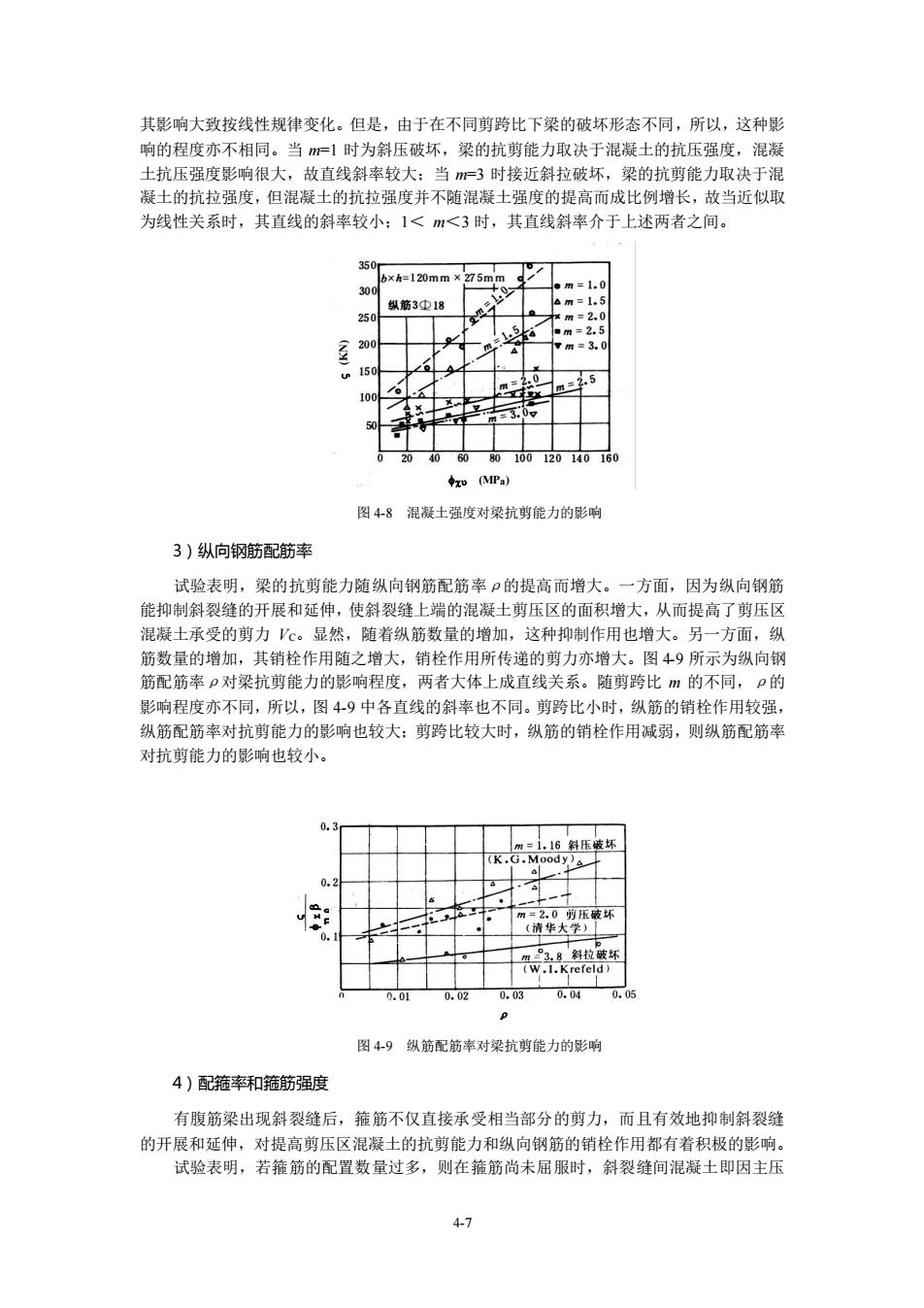
其影响大致按线性规律变化。但是,由于在不同剪跨比下梁的破坏形态不同,所以,这种影形 响的程度亦不相同。当1时为斜压破坏,梁的抗剪能力取决于混凝士的抗压强度,混 士抗压强度影响很大 故直线斜率较大:当m3时接近斜拉破坏,梁的抗剪能力取决于混 凝土的抗拉强度,但混凝士的抗拉强度并不随混凝士强度的提高而成比例增长,故当近似取 为线性关系时,其直线的斜*较小:1<m<3时,其直线斜率介于上述两者之间。 50 b×h=120mm×275mn 000204010 图48混凝土强度对梁抗剪能力的影响 3)纵向钢筋配筋率 试验表明,梁的抗剪能力随纵向钢筋配筋率ρ的提高而增大。一方面,因为纵向钢筋 能抑制斜裂缝的开展和延伸,使斜裂缝上端的混凝土剪压区的面积增大,从而提高了剪压区 混凝土承受的剪力。显然,随着纵筋数量的增加,这种抑制作用也增大。另一方面,纵 饰勒量的增加,其销栓作用随之瑞大,销栓作用所估递的前力亦增大。图49所示为纵向钢 筋配筋率P对梁抗剪能力的影响程度,两者大体上成直线关系。 随剪跨比m的不同, P的 影响程度亦不同,所以,图49中各直线的斜率也不同。剪跨比小时,纵筋的销栓作用较强 纵筋配筋率对抗剪能力的影响也较大:剪跨比较大时,纵筋的销栓作用减弱,则纵筋配筋率 对抗剪能力的影响也较小。 1.16斜压坏 请华大 8 .01 0.03 0, 图49纵筋配筋率对梁抗剪能力的影响 4)配籍率和箍筋强度 有腹筋梁出现斜裂缝后,箍筋不仅直接承受相当部分的剪力,而且有效地抑制斜裂缝 的开展和延伸,对提高剪压区混凝土的抗剪能力和纵向钢筋的销栓作用都有着积极的影响。 试验表明,若箍筋的配置数量过多,则在箍筋尚未屈服时,斜裂缝间混凝士即因主压 41
4-7 其影响大致按线性规律变化。但是,由于在不同剪跨比下梁的破坏形态不同,所以,这种影 响的程度亦不相同。当 m=1 时为斜压破坏,梁的抗剪能力取决于混凝土的抗压强度,混凝 土抗压强度影响很大,故直线斜率较大;当 m=3 时接近斜拉破坏,梁的抗剪能力取决于混 凝土的抗拉强度,但混凝土的抗拉强度并不随混凝土强度的提高而成比例增长,故当近似取 为线性关系时,其直线的斜率较小;1< m<3 时,其直线斜率介于上述两者之间。 图 4-8 混凝土强度对梁抗剪能力的影响 3)纵向钢筋配筋率 试验表明,梁的抗剪能力随纵向钢筋配筋率ρ的提高而增大。一方面,因为纵向钢筋 能抑制斜裂缝的开展和延伸,使斜裂缝上端的混凝土剪压区的面积增大,从而提高了剪压区 混凝土承受的剪力 VC。显然,随着纵筋数量的增加,这种抑制作用也增大。另一方面,纵 筋数量的增加,其销栓作用随之增大,销栓作用所传递的剪力亦增大。图 4-9 所示为纵向钢 筋配筋率ρ对梁抗剪能力的影响程度,两者大体上成直线关系。随剪跨比 m 的不同,ρ的 影响程度亦不同,所以,图 4-9 中各直线的斜率也不同。剪跨比小时,纵筋的销栓作用较强, 纵筋配筋率对抗剪能力的影响也较大;剪跨比较大时,纵筋的销栓作用减弱,则纵筋配筋率 对抗剪能力的影响也较小。 图 4-9 纵筋配筋率对梁抗剪能力的影响 4)配箍率和箍筋强度 有腹筋梁出现斜裂缝后,箍筋不仅直接承受相当部分的剪力,而且有效地抑制斜裂缝 的开展和延伸,对提高剪压区混凝土的抗剪能力和纵向钢筋的销栓作用都有着积极的影响。 试验表明,若箍筋的配置数量过多,则在箍筋尚未屈服时,斜裂缝间混凝土即因主压 (KN) (MPa) ρ

应力过大而发生斜压破坏。此时梁的抗剪能力取决于构件的截面尺寸和混凝士强度,并与无 腹筋梁斜压破坏时的抗剪能力相接近。 若箍筋的配置数量远 斜裂缝出现后,原来由混凝土承受的拉力转由与斜裂缝相 交的箍筋承受,在箍筋尚未屈服时,由于箍筋的作用,延缓和限制了斜裂缝的开展和延伸 承载力尚能有较大的增长。当箍筋屈服后,其变形迅速增大,不再能有效地抑制斜裂缝的开 展和延伸,最后,斜裂缝上端的混凝土在剪、压复合应力作用下达到极限强度,发生剪压破 坏。此时,梁的抗剪能力主要与混凝土强度和箍筋配置数量有关,而剪跨比和纵筋配筋率等 因素的影响相对较 若箍筋配置数量过少,则斜裂缝一出现,截面即发生急剧的应力重分布 原来由混凝 土承受的拉力转由箍筋承受,使箍筋很快达到屈服,变形剧增,不能抑制斜裂缝的开展,此 时梁的破坏形态与无腹筋梁相似。当剪跨比较大时,也将产生脆性的斜拉破坏。 箍筋用量一般用箍筋配筋率(工程上习惯称配箍率)P(%)表示,即 (4-2) 式中A。一一斜截面内配置在沿梁长度方向一个箍筋间矩3,范围内的箍筋各肢总截面积: b一一截面宽度,对T形裁面梁取b为肋宽: S,一一沿梁长度方向箍筋的间距 图410表示配箍率与箍筋抗拉强度的乘积对梁抗剪能力的影响。当其它条件相同时, 两者大体成线性关系。 由于梁斜截面破坏属于脆性破坏,为了提高斜截面延性,不宜采用高强钢筋作箍筋。 (MPa) 图410配箍率对梁抗剪能力的影响 4.3受弯构件的斜截面抗剪承载力 加前所述,钢筋混土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和前压破坏 面抗剪承载力 的计算。《公路桥规》的基本公式就是针对这种破坏形态的受力特征而建立的。 4.3.1斜截面抗剪承载力计算的基本公式及适用条件 4-8
4-8 应力过大而发生斜压破坏。此时梁的抗剪能力取决于构件的截面尺寸和混凝土强度,并与无 腹筋梁斜压破坏时的抗剪能力相接近。 若箍筋的配置数量适当,则斜裂缝出现后,原来由混凝土承受的拉力转由与斜裂缝相 交的箍筋承受,在箍筋尚未屈服时,由于箍筋的作用,延缓和限制了斜裂缝的开展和延伸, 承载力尚能有较大的增长。当箍筋屈服后,其变形迅速增大,不再能有效地抑制斜裂缝的开 展和延伸,最后,斜裂缝上端的混凝土在剪、压复合应力作用下达到极限强度,发生剪压破 坏。此时,梁的抗剪能力主要与混凝土强度和箍筋配置数量有关,而剪跨比和纵筋配筋率等 因素的影响相对较小。 若箍筋配置数量过少,则斜裂缝一出现,截面即发生急剧的应力重分布,原来由混凝 土承受的拉力转由箍筋承受,使箍筋很快达到屈服,变形剧增,不能抑制斜裂缝的开展,此 时梁的破坏形态与无腹筋梁相似。当剪跨比较大时,也将产生脆性的斜拉破坏。 箍筋用量一般用箍筋配筋率(工程上习惯称配箍率) sv (%)表示,即 v sv sv bS A = (4-2) 式中 Asv ——斜截面内配置在沿梁长度方向一个箍筋间矩 v s 范围内的箍筋各肢总截面积; b ——截面宽度,对 T 形截面梁取 b 为肋宽; v S ——沿梁长度方向箍筋的间距。 图 4-10 表示配箍率与箍筋抗拉强度的乘积对梁抗剪能力的影响。当其它条件相同时, 两者大体成线性关系。 由于梁斜截面破坏属于脆性破坏,为了提高斜截面延性,不宜采用高强钢筋作箍筋。 图 4-10 配箍率对梁抗剪能力的影响 4.3 受弯构件的斜截面抗剪承载力 如前所述,钢筋混凝土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和剪压破坏 等。在设计时,对于斜压和斜拉破坏,一般是采用截面限制条件和一定的构造措施予以避免。 对于常见的剪压破坏形态,梁的斜截面抗剪力变化幅度较大,故必须进行斜截面抗剪承载力 的计算。《公路桥规》的基本公式就是针对这种破坏形态的受力特征而建立的。 4.3.1 斜截面抗剪承载力计算的基本公式及适用条件 =34MPa ρ

配有箍筋和弯起钢筋的钢筋混凝土梁,当发生剪压破坏时,其抗剪承载力人。是由剪压 区混凝土抗剪力,箍筋所能承受的剪力V和弯起钢筋所能承受的剪力V。所组成(图 411),即 V=V+V+Vs (43) 飞nfV an v da 图4+1斜面抗剪承载力计算图式 在有腹筋梁中,箍筋的存在抑制了斜裂缝的开展,使剪压区面积增大,导致了剪压区 混凝土抗剪能力的提高,其提高程度与箍筋的抗拉强度和配箍率有关。因而,式(4-3)中 的V。与V,是紧密相关的,但两者目前尚无法分别予以精确定量,而只能用V来表达混凝 土和箍筋的综合抗剪承载力,即 (4-4) 《公路桥规》根据国内外的有关试验资料,对配有腹筋的钢筋混凝土梁斜截面抗剪承 载力的计算采用下述半经验半理论的公式: YoVV=aaza(0.45x10)bh(2+0.6p)fpf +0.75x10-3)fΣAsn6, (45) 式中 V。一一斜截面受压端正截面上由作用(或荷载)效应所产生的最大剪力组合 设计值(kN): Y。一一桥梁结构的重要性系数 一一异号弯矩影响系数。计算简支梁和连续梁近边支点梁段的抗剪承载力时, =1.0:计算连续梁和悬臂梁近中间支点梁段的抗剪承载力时,0.9: 一一预应力提高系数(详见第13章)。对钢筋混凝土受弯构件,,=1: a -一受压翼缘的影响系数。对具有受压翼缘的截面,取心,=1.1: b 斜截面受压区顶端截面处矩形截面宽度(mm),或T形和I形裁面腹板究 度(mm: h,一一斜截面受压端正截面上的有效高度,自纵向受拉钢筋合力点到受压边缘的 距离(mm): 4-9
4-9 配有箍筋和弯起钢筋的钢筋混凝土梁,当发生剪压破坏时,其抗剪承载力 Vu 是由剪压 区混凝土抗剪力 Vc,箍筋所能承受的剪力 Vsv 和弯起钢筋所能承受的剪力 Vsb 所组成(图 4-11),即 Vu =Vc +Vsv +Vsb (4-3) 图 4-11 斜截面抗剪承载力计算图式 在有腹筋梁中,箍筋的存在抑制了斜裂缝的开展,使剪压区面积增大,导致了剪压区 混凝土抗剪能力的提高,其提高程度与箍筋的抗拉强度和配箍率有关。因而,式(4-3)中 的 Vc与 Vsv是紧密相关的,但两者目前尚无法分别予以精确定量,而只能用 Vcs 来表达混凝 土和箍筋的综合抗剪承载力,即 Vu =Vcs +Vsb (4-4) 《公路桥规》根据国内外的有关试验资料,对配有腹筋的钢筋混凝土梁斜截面抗剪承 载力的计算采用下述半经验半理论的公式: 0Vd ≤ ( ) ( ) 3 1 2 3 0 , 0.45 10 2 0.6 V bh p f f u cu k sv sv − = + ( ) sd Asb s 0.75 10 f sin 3 + − (4-5) 式中 V d ——斜截面受压端正截面上由作用(或荷载)效应所产生的最大剪力组合 设计值(kN); 0 ——桥梁结构的重要性系数; 1 ——异号弯矩影响系数。计算简支梁和连续梁近边支点梁段的抗剪承载力时, 1 =1.0;计算连续梁和悬臂梁近中间支点梁段的抗剪承载力时, 1 =0.9; 2 ——预应力提高系数(详见第 13 章)。对钢筋混凝土受弯构件, 2 =1; 3 ——受压翼缘的影响系数。对具有受压翼缘的截面,取 3 =1.1; b ——斜截面受压区顶端截面处矩形截面宽度(mm),或 T 形和 I 形截面腹板宽 度(mm); 0 h ——斜截面受压端正截面上的有效高度,自纵向受拉钢筋合力点到受压边缘的 距离(mm);

p一一斜截面内纵向受拉钢筋的配筋率,p=100p,p=A/bh,当p>2.5 时,取p=2.5: ∫一一混凝土立方体抗压强度标准值(MPa): P,—箍筋配筋率,见式(4-2): 厂—箍筋抗拉强度设计值(MPa): ∫a一一弯起钢筋的抗拉强度设计值(MPa): A,。一斜截面内在同一个弯起钢筋平面内的弯起钢筋总截面面积(mm): 日,一一弯起钢筋的切线与构件水平纵向轴线的夹角。 这里要指出以下几点: (1)式(45)所表达的斜截面抗剪承载力中,混凝土和箍筋提供的综合抗剪承载力为 V。=aa,a,(0.45×10)(2+0.6p)V厂Pnfn,弯起钢筋提供的抗剪承载力为 V=0.75×103)/aΣ4,sn0,。当不设弯起钢筋时,梁的斜截面抗剪力Y,等于V。。 (2)式(45)是一个半经验半理论公式,使用时必须按规定的单位代入数值,而计算 得到的斜截面抗剪承载力V的单位为kN。 式(45)是根据剪压破坏形态发生时的受力特征和试验资料而制定的,仅在一定的条 件下才适用,因而必须限定其适用范围,称为计算公式的上、下限值。 1)上限值—截面最小尺寸 当梁的截面尺寸较小而剪力过大时,就可能在梁的肋部产生过大的主压应力,使梁发生 斜压破坏(或梁肋板压坏)。这种梁的抗剪承载力取决于混凝士的抗压强度及梁的截面尺寸 不能用增加腹筋数量来提高抗剪承载力。《公路桥规》规定了截面最小尺寸的限制条件,这 种限制,同时也为了防止梁在使用阶段斜裂缝开展过大,特别是薄腹梁。截面尺寸应满足: y'a≤0.51×10-fnxbh (kN) (4-6) 式中V。一一验算截面处由作用(或荷载)产生的剪力组合设计值(kN): ∫一一混凝土立方体抗压强度标准值(MPa): b一一相应于剪力组合设计值处矩形截面的宽度(mm),或T形和1形截面腹板宽 度(mm): 么一一相应于剪力组合设计值处截面的有效高度(mm)。 若式(4-6)不满足,则应加大截面尺寸或提高混凝土强度等级。 2)下限值—按构造要求配置箍筋 4.10
4-10 p ——斜截面内纵向受拉钢筋的配筋率, p =100 , = A bh s 0 ,当 p >2.5 时,取 p =2.5; cu k f , ——混凝土立方体抗压强度标准值(MPa); sv ——箍筋配筋率,见式(4-2); sv f ——箍筋抗拉强度设计值(MPa); sd f ——弯起钢筋的抗拉强度设计值(MPa); Asb ——斜截面内在同一个弯起钢筋平面内的弯起钢筋总截面面积(mm2); s ——弯起钢筋的切线与构件水平纵向轴线的夹角。 这里要指出以下几点: (1)式(4-5)所表达的斜截面抗剪承载力中,混凝土和箍筋提供的综合抗剪承载力为 ( ) ( ) 3 1 2 3 , 0.45 10 2 0.6 V p f f cs cu k sv sv − = + ,弯起钢筋 提 供的 抗 剪 承 载力 为 ( ) sb sd Asb s V 0.75 10 f sin 3 = − 。当不设弯起钢筋时,梁的斜截面抗剪力 Vu 等于 Vcs 。 (2)式(4-5)是一个半经验半理论公式,使用时必须按规定的单位代入数值,而计算 得到的斜截面抗剪承载力 Vu 的单位为 kN。 式(4-5)是根据剪压破坏形态发生时的受力特征和试验资料而制定的,仅在一定的条 件下才适用,因而必须限定其适用范围,称为计算公式的上、下限值。 1)上限值——截面最小尺寸 当梁的截面尺寸较小而剪力过大时,就可能在梁的肋部产生过大的主压应力,使梁发生 斜压破坏(或梁肋板压坏)。这种梁的抗剪承载力取决于混凝土的抗压强度及梁的截面尺寸, 不能用增加腹筋数量来提高抗剪承载力。《公路桥规》规定了截面最小尺寸的限制条件,这 种限制,同时也为了防止梁在使用阶段斜裂缝开展过大,特别是薄腹梁。截面尺寸应满足: 0Vd ≤ ( ) , 0 3 0.51 10 f cu k bh − (kN) (4-6) 式中 Vd ——验算截面处由作用(或荷载)产生的剪力组合设计值(kN); cu k f , ——混凝土立方体抗压强度标准值(MPa); b ——相应于剪力组合设计值处矩形截面的宽度(mm),或 T 形和 I 形截面腹板宽 度(mm); 0 h ——相应于剪力组合设计值处截面的有效高度(mm)。 若式(4-6)不满足,则应加大截面尺寸或提高混凝土强度等级。 2)下限值——按构造要求配置箍筋