
第7卷第4期 智能系统学报 Vol.7 No.4 2012年8月 CAAI Transactions on Intelligent Systems Aug.2012 D0I:10.3969/j.issn.1673-4785.201112019 网络出版地址:htp:/nw.cmki.net/kcms/detail/23.1538.TP.20120712.1137.011.html 相关向量机分类方法的研究进展与分析 赵春晖,张燚 (哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001) 摘要:相关向量机(RVM)是一种基于贝叶斯模型的监督机器学习算法,可用于处理回归以及分类问题。与支持向 量机(SVM)相比,相关向量机的优点在于其输出结果是一种概率模型,其相关向量的个数远远小于支持向量的个 数,并且测试时间短.总结了相关向量机的基本原理及主要应用领域,详细阐述了相关向量机的模型结构以及分类 方法,重点介绍了在高光谱图像分类中的应用.并针对RVM算法在高光谱图像分类中的不足,给出了多种改进方 案,并作以比较.希望对研究者今后的研究有所启发,以促进该领域的发展 关键词:相关向量机;改进型相关向量机;高光谱图像;分类算法 中图分类号:TP751.1文献标志码:A文章编号:1673-4785(2012)04029408 Research progress and analysis on methods for classification of RVM ZHAO Chunhui,ZHANG Yi College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China) Abstract:The relevance vector machine(RVM)is a machine learning algorithm which is based on supervision of a Bayesian model.It can be used to deal with regression and classification problems.Compared with the support vec- tor machine (SVM),the relevance vector machine has the advantage that its output is a probability model and the number of relevance vectors is far fewer than the number of support vectors.In this paper,the application was sum- marized with a relevance vector machine and the classification of a hyperspectral image with RVM was introduced; the RVM model and the method of classification were also explained.In light of the disadvantage of classification, some improved methods were summarized.Various methods were generalized and analyzed while attempting to find breakthroughs and promote further research. Keywords:relevance vector machine;improved relevance vector machine;hyperspectral image;classification algorithm 机器学习在人工智能的研究中具有十分重要的 习能力之间寻求最佳折衷,是监督分类的典型代表, 地位.其应用已遍及人工智能的各个分支,如专家系 已经成为模式识别以及机器学习研究领域比较领先 统、自动推理、自然语言理解、模式识别、计算机视 的方法之一.但SVM仍存在着一定的局限性:1)支 觉、智能机器人等领域.其中尤为典型的是专家系统 持向量的数量会随着训练样本数量的增加而线性增 中的知识获取瓶颈问题,人们一直试图采用机器学 加,这样会导致分类效率降低,训练时间过长;2)预 习的方法加以解决 测结果没有后验概率,无法通过结果观测到分类的 支持向量机(support vector machine,SVM)四 准确度;3)对于给定的误差参数,主观性过强,容易 是由Vappnik于1995年提出的,建立在统计学理论 造成主观误差;4)核函数必须满足Mercer条件[231. 和结构风险最小原理的基础上,在模型复杂性与学 相关向量机(relevance vector machine, RVM)1,是Tipping于2O01年提出的一种与SVM 收稿日期:2011-12-30.网络出版日期:201207-12 类似的稀疏概率模型.它可以在保证分类精度与 基金项目:国家自然科学基金资助项目(61077079):教育部博士点基 SVM相同的情况下,提供一个后验概率分布.与 金资助项目(20102304110013). 通信作者:赵春晖.E-mail:zhaochunhuic@hrbeu.edu.cn. SVM相比,相关向量的个数远远小于支持向量的个

第4期 赵春晖,等:相关向量机分类方法的研究进展与分析 ·295· 数,并且其核函数也不需要满足Mercer条件.但是 数,也需要加入噪声函数σ2.这个函数属于一种刻 RVM在解决以上SVM问题的同时也引入了新的问 度函数,其分布满足伽玛分布: 题.当RVM应用于高光谱图像分类时,由于高光谱 图像数据样本大、维数高5],会使分类过程中的训 p()=Gamma(aI a,6), 练时间随着样本复杂度的增加而直线上升,严重影 p(B)=Gamma(BI c,d). 响了分类的效率.因此Bishop等提出一种改进型相 式中:B=σ2,并且 关向量机方法6,该方法主要是通过引人一个新的 Gamma(al a,b)=I(a)ba-e-ba 概率分布,降低训练过程中的运算复杂度,提高分类 效率,在小样本情况下有较好的分类精度。 式中:ra)=re出为伽马函数为了确保这 些参数是无先验知识的,规定它们的取值很小,如 1相关向量机理论 a=b=c=d=104.若将这些参数设为0,则会获 1.1相关向量机模型 得均匀的超参数.在大多数的文献中一般取a= b=c=d=0. 如果输入数据组为{xm,tn}01,并且考虑到目标 函数只是一个标量,根据标准概率方程式,假设目标 1.2相关向量机回归方法 函数是模型的样本并且附加着噪声: 在超参数估计的收敛过程中,预测部分是基于 t y(x;w)+8. (1) 后验概率模型的加权,并且找到最大化的c与 式中:8.是零均值的高斯噪声,并且相互独立,其方 σi·然后根据 差为o2.因此表达式p(tn|x)=N(tnly(x),o2)是 p(t;I t)=p(t:I w,a,2)p(w,a,o21 t)dwdado? 服从高斯分布的表达式,其分布由。和y(xn)的值 计算分布的预测.对于一个新的参数x:,利用 以及方差σ2决定.而其中y(x)是一个由核函数决 p(w|t,a,o2)=(2m)-(wn|Σ1-1n. 定的值,并且核函数由训练样本中:(x)=K(x,x:)决 定.假设t。是相互独立的,则样本数据的完整概率 ep{-2(w-u)'(w-u)} 表达式可以写为 可以得到 ()-(2)exp(tw p(|t,ar,ie)= (2) 式中:t=[t12…tw]T,w=[01…0w]T和更都是 p(t:I w,cup)p(wl t,awp,oue)dw 预先设计好的大小为W×(N+1)的矩阵,并且Φ= 可简化为 [中(x1)中(x2)…中(xw)]的值为中(xn)= p(t;l t,aup,om)N(tiI yi,). [1K(xn,x)K(xn,x2)…K(x.,xN)]T为了使表达 式中: 式更加简单化,在式(2)中忽略一些隐含的输入数 yi=u(),i=ip+()(). 据{xn. 所以预测的含义就是直观地得到y(x:),或 随着训练样本中参数被大量地使用,在进行w 者通过后验权均值预测基础函数的权值,其中很多 和σ2的最大似然估计时会产生过适应现象.为了避 基础函数的权值都是0.数据中的噪声估计决定了 免这种现象的发生,可以对一些参数加入一定附加 预测权值的不确定性, 强制条件.这种作法已经在SVM中大量使用,并且 1.3相关向量机分类方法 非常有效。 相关向量机分类方法就是一种拉普拉斯逼近的 在RVM中采用贝叶斯透视方法作为强制条 回归算法8 件.定义一个的比较简单的函数,这个函数是一 若需要预测输人x的部分后验概率,可根据统 个应用广泛的零均值的高斯概率分布: 计学原理,利用函数σ(y)=1/(1+e)对线性模 型y(x)进行归一化,其中p(t|x)是一个贝努利分 p(wa)=ΠN(o:l0,a'). (3) 布,其分布表达式为 对于每一个权重来说,式(3)中都存在独立分 布的参数,可以极大地缓解之前分布的复杂度6, p(Iw)=Πoy(x,;w)5· 定义一个超参数α,同样地为了匹配最后的函 [1-o{y(xn;w)}]1-. (4)

·296 智能系统学报 第7卷 式中:根据概率定义,目标函数tn∈{0,1,需要注 地找到感兴趣的目标刃 意式(4)中并没有附加的噪声函数. 之后Gholami等于2010年将RVM应用在新生 分类过程中,不能利用卷积方式计算权重,所以 儿痛苦评价上,成功地对新生儿痛苦表情进行分类, 并不能给出p(wlt,a)或边缘分布p(ta)的解析 正确区分了痛苦与非痛苦的婴儿,并且对痛苦程度 解.因此,需要利用拉普拉斯逼近的近似解求得,具 进行区分8].需要注意的是,该方法也是基于新生 体过程如下: 儿表情的数字图像处理,大多归结为回归或者分类 1)首先固定α的值,给出模型的后验概率分布 的问题,因此相关向量机在该领域的应用是很有前 位置,得到权重wP的最可能值.因为p(w|t,)c 景的. p(tw)p(wla),所以这一过程等价于找到式(5)的 2.2数字图像处理 最小值 对于一般数字图像处理,相关向量机的应用也 Igip(t,w)p(wl a)= 主要分为处理回归和处理分类问题两大方面, [,lg.+(1-6)lg(1-x)】-2w 在处理回归问题中,Agarwal等9在2006年、Guo 等o在2007年、Sedai等1]在2009年、Guo等2在 (5) 2009年,将RVM应用于人类3-D图像从单眼图像恢复 式中:y.=o{y(x;w)},应用最小平方反复迭代方 过程中,该算法主要应用了RVM的回归理论,通过真 法得到W如的值. 实数据的训练,RVM回归机可以正确捕捉人体行动,算 2)拉普拉斯方法是利用一个简单的二次方程 法可以将正确率提高到90%左右.0 uyang等在2009 逼近Lg分布的方法.其值是通过二次变形给出: 年,将RVM应用于网络视频监控技术,结果表明,采用 7 wVolgp(w|t,a)lwp=-(ΦBΦ+A). 了RVM回归算法的网络视频监视系统可以较快速地 (6) 找到人体框架,并且RVM的寻找速度要比其他方法更 式中:B=diag(B1,B2,…,Bw)是一个对角线矩阵,其 快,尤其在测试进行一段时间之后,其分辨的正确率也 中Bn=σ(y(xn))[1-σ(y(xn))].对于高斯逼近 很高,可达到80%以上1.0 Dliveri等在2011年将RVM 来说权重主要集中在"P,并且通过式(6)可以得到 应用于图像恢复中.研究表明,将快速RVM算法与其 协方差矩阵 他算法相结合,其图像恢复效果更好,运算速度也较 3)利用∑的统计学和w的高斯逼近(代替 快4 在分类处理方法中X.Li等s]和X.Wang μ),超参数a可以利用-Y来更新 等61在2009年将RVM应用于图像分类比较中,实 在模型p(wIt,a)中,利用式(6)以及 验结果表明RVM分类方法对于线性数据以及非线 7,lgp(wlt,a)lwe=0,可以得到 性的高维数据都具有较好的分类效果, =(DB电+A), (7) 2.3高光谱图像分类 Wup =oBt. (8) 由于高光谱图像样本数量大、维数较高等特点, 式(7)和(8)可用于解决最小二乘问题.可以看 相关向量机分类方法非常适合应用于高光谱图像分 出拉普拉斯逼近方法能够有效地将分类问题映射为 类.Demir等于2007年在高光谱图像分类中应用了 回归问题. RVM方法,详细阐述了RVM方法与SVM方法的不 同,并且比较了分类结果,利用分类精度、相关向量和 2相关向量机的应用 支持向量的个数等标准,评价了各自优缺点「.随后 因为相关向量机可用于回归以及分类问题,所 Mianji等在2011年又进一步比较了RVM方法与 以其应用非常广泛.目前国内外主要应用领域有以 SVM方法在高光谱图像分类中的性能,比较的标准 增加了训练时间以及测试时间].通过实验发现 下几方面. RVM方法与SVM方法在训练样本相同时,其分类精 2.1医学影像处理 相关向量机在医学领域中的主要应用是对数字 度基本一致,但相关向量的数量明显少于支持向量的 医学图片的分析.首先Lkic等在2007年将RVM 数量.在测试时间方面,RVM的测试时间非常短,几 应用在分析神经成像之中,所采用的RVM方法与 乎可以做到实时测试,而SVM的测试时间相对较长. 处理一般图像的现有方法有着相近的效果,然而 然而RVM的缺点在于随着训练样本的增加,其训练 RVM的复杂度比其他方法要低很多,并且可以准确 时间也会直线上升.分析比较结果如表12

第4期 赵春晖,等:相关向量机分类方法的研究进展与分析 297. 表1分类精度比较 综合式(11)和式(12),则Q(0)就是P(01D)的近似 Table 1 The accuracy of classification 边缘概率分布,通过该近似的方法,只要选择一个合 SVM RVM 适的分布Q,L(Q)的值即便在传统证据模型函数未 训练 测试 样本 样本 分类 支持 分类 支持 知的情况下也可以通过简单的计算得到.因此改进 精度/%向量数 精度/%向量数 型RVM的方法就是选择一个形式较为简单的Q (0),使得L(Q)的计算较为简单,并且同时保证L 590 4588 84.39 937 80.95 192 (Q)的形式足够灵活 1320 4588 87.941510 84.45 254 根据式(9)且考虑到参数0的变形形式{0:}, 2376 4588 90.56 2217 87.05 353 则Q(0)可以定义为 4757 4588 92.673393 90.32 592 Q(0)=ΠQ.(0). 式中: 表2分类时间 Table 2 The time of classification Q(0)= exp(InP(D,0)>xzi (13) SVM exp<InP(D,0)>::d0: RVM 样本数量 训练时间测试时间 训练时间测试时间 式中:〈·)k定义为对于Q(0)分布(其中k≠) 的期望.可以证明,如果概率模型中的每个因素 230 2.2 2.6 13.5 0.39 Q:(0:)可以用一种带有节点的有向循环图来表示, 693 3 3.6 49.2 0.40 那么Q:(0:)的解就仅仅取决于Q分布的变量形 2967 19.5 25.6 1718 3.40 式[201 3500 21.4 27.6 1806 3.90 式(13)的右半部分取决于Qk:的任意时刻,所 为了克服RVM在高光谱图像分类中存在的缺点, 以式(13)是Q:(0:)的一种特殊的求解表达式.又因 根据RVM自身特点,下面给出了多种改进方案, 为Q:(0:)是共轭的条件分布,因此可以通过计算得 到在所需时刻的标准条件分布.然后通过初始化,循 3相关向量机分类方法的改进 环使用式(13),迭代更新变量,最终得到Q的所有 3.1改进型相关向量机 分布. 3.1.1改进型相关向量机模型 3.1.2改进型相关向量机分类算法 传统的概率模型可以将随机变量分为观测数据D 输入数据边缘概率的对数形式为 和非观测变量日6,].观测数据D的边缘概率密度为 InP(TI X)=InP(TI X,w)P(wIa)P(a)dwda. P(D)=P(D,8)d0. (9) 利用之前处理结论和近似的分解变量形式Q(w) 对于式(9)的积分计算,通常来说较为复杂.因 Q(ax),并结合式(11),将上式近似为 此改进思想是通过引入近似的分布Q(),其中对 InP(TIX)=JJQ.(w)Q.(a). 于任意选择的非观测变量0,可以将边缘概率密度 的积分形式分解为2个对数之和,即将式(9)近似 In(mde.(4) Q.(w)Q.(a) 分解为 式(14)的积分计算会增加运算的复杂度,因此根据 InP(D)L(Q)+K(QI P). (10) Jaakkola等21的分析方法,引入 式中: σ(y)[1-o(y)]l-=c(z)≥ L(Q)=[Q()Do. Q(8) (11) ()em-AE2-小 (15) 引入的分布Q(0)是P(D,0)和后验分布 式中:z=(2t-1)y,入(5)=(1/45)tanh(/2).专是 K,(QIP)之间的Kullback-Leibler距离差,表达式如 一个可变的参数,当等号成立时,可以得到专=云,将 式(12) 式(15)代入相关向量机模型中,可以得到 K(QIP)=-Q()(D)o. (12) P(T1X,w)≥F(T,X,w,) Q(0) 式中:K(Q1P)≥0.式(10)的右半部分是Q的独 Πo()em2车-A(5.)公- 立分布,因此最大化L(Q)等同于最小化K(Q1P). (16)
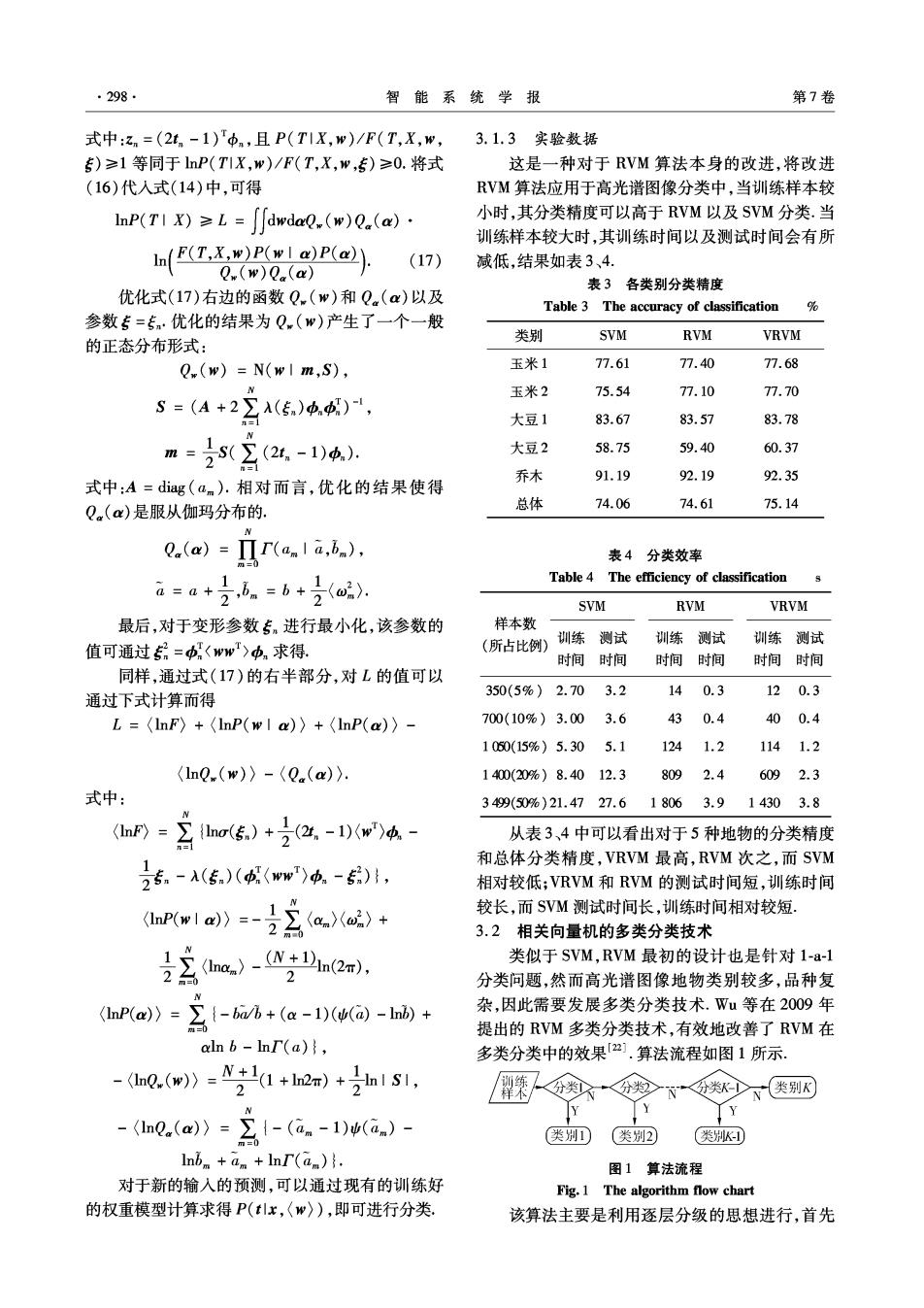
·298· 智能系统学报 第7卷 式中:zn=(2tn-1)中,且P(T1X,w)/F(T,X,w, 3.1.3实验数据 )≥1等同于lnP(T1X,w)/F(T,X,w,)≥0.将式 这是一种对于RVM算法本身的改进,将改进 (16)代入式(14)中,可得 RVM算法应用于高光谱图像分类中,当训练样本较 hF(T1X)≥L=j∬awda0.(w)Q.(a)· 小时,其分类精度可以高于RVM以及SVM分类.当 训练样本较大时,其训练时间以及测试时间会有所 I(E(T.X.w)P(wla)P(a)). (17) 减低,结果如表3、4. Q(w)Q(a) 表3各类别分类精度 优化式(17)右边的函数Q.(w)和Q.(a)以及 Table 3 The accuracy of classification % 参数专=专·优化的结果为Q(w)产生了一个一般 类别 SVM VRVM 的正态分布形式: RVM Q.(w)=N(w1m,S), 玉米1 77.61 77.40 77.68 玉米2 75.54 77.10 77.70 S=(A+2∑A(5)中,中)1, 大豆1 83.67 83.57 83.78 =23含(24.-100). m 大豆2 58.75 59.40 60.37 91.19 92.19 92.35 式中:A=dig(am).相对而言,优化的结果使得 乔木 Q.(a)是服从伽玛分布的. 总体 74.06 74.61 75.14 .(am)=ra.1a,b., 表4分类效率 a=a+3,。=6+2(2. Table 4 The efficiency of classification SVM RVM VRVM 最后,对于变形参数专.进行最小化,该参数的 样本数 (所古比例) 训练测试 训练测试 训练测试 值可通过=中ww>中n求得, 时间时间 时间时间 时间时间 同样,通过式(17)的右半部分,对L的值可以 350(5%)2.70 3.2 140.3 120.3 通过下式计算而得 L=lnF)〉+〈lnP(wIa)〉+〈lnP(a)〉- 700(10%)3.00 3.6 430.4 400.4 1050(15%)5.305.1 1241.2 1141.2 lnQw(w)〉-〈Q.(a)). 1400(20%)8.4012.38092.4 6092.3 式中: 3499(50%)21.4727.618063.914303.8 =三ha5.)+2,-Dw4- 从表3、4中可以看出对于5种地物的分类精度 和总体分类精度,VRVM最高,RVM次之,而SVM 2点.-A(5)((wm)0,-6), 相对较低;VRVM和RVM的测试时间短,训练时间 hPw1m》=-2ga.i)+ 较长,而SVM测试时间长,训练时间相对较短, 3.2相关向量机的多类分类技术 2m)-hea. 类似于SVM,RVM最初的设计也是针对1-a-1 2 分类问题,然而高光谱图像地物类别较多,品种复 (hPam》=名-bah+(a-1w(a-lh+ 杂,因此需要发展多类分类技术.Wu等在2009年 提出的RVM多类分类技术,有效地改善了RVM在 aln b -InI(a), 多类分类中的效果[2].算法流程如图1所示。 -0.(m》-w2'1+h2m)+21s1. <分 分N分类少(类别E Y -(lnQ(a)〉=∑{-(an-1)(an)- Y m=0 类别1) (类捌2 (类州K幻 Inbm +am Inl(am). 图1算法流程 对于新的输入的预测,可以通过现有的训练好 Fig.1 The algorithm flow chart 的权重模型计算求得P(tx,〈),即可进行分类. 该算法主要是利用逐层分级的思想进行,首先