
Mason's Gain Formula To find the relationship between an input variable and an output variable. Total transfer function:. P=人∑RA ·△=determinant of the graph =1-(sum of individual loop gains)+(sum of gain products of two nontouching loops)-(sum of gain products of all possible combinations of three nontouching loops)-... A=1-∑L+∑LL。-∑LgL:Ly+ d,e,]
Mason’s Gain Formula • To find the relationship between an input variable and an output variable. Total transfer function: • Δ=determinant of the graph k P Pk k 1 =1-(sum of individual loop gains) + (sum of gain products of two nontouching loops) – (sum of gain products of all possible combinations of three nontouching loops)-… 1 ... , , , d e f d e f b c b c a L a L L L L L
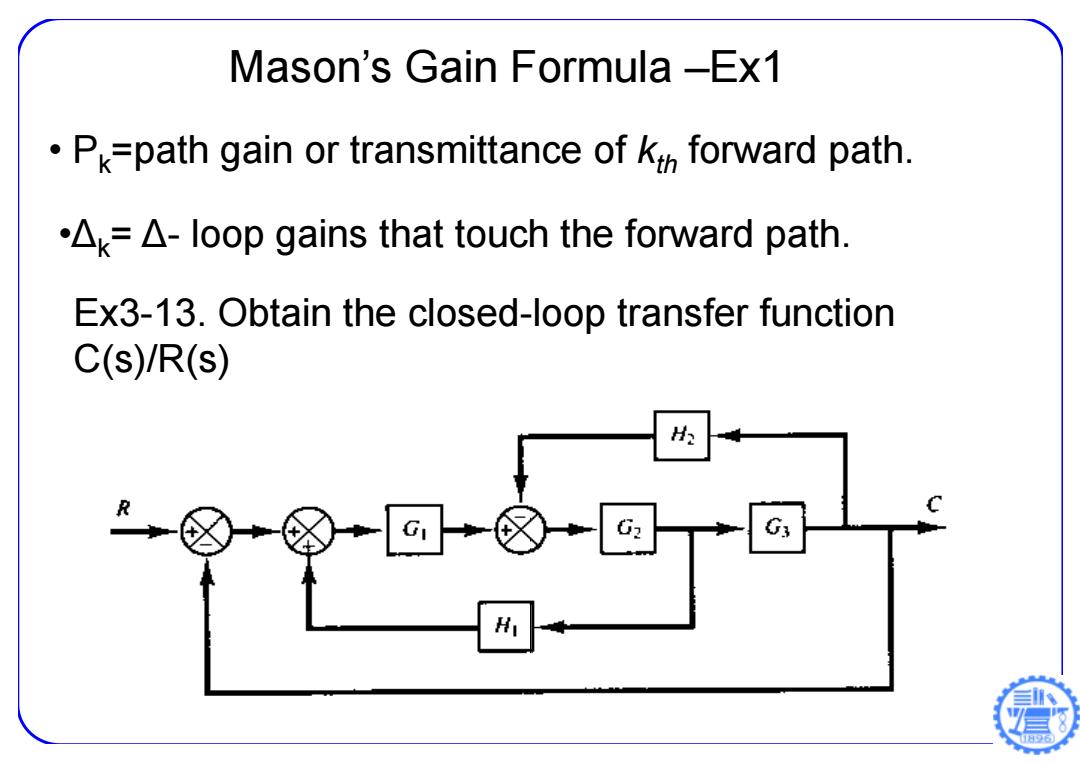
Mason's Gain Formula -Ex1 P=path gain or transmittance of k;forward path. △k=△-loop gains that touch the forward path. Ex3-13.Obtain the closed-loop transfer function C(s)/R(s) H G H
Mason’s Gain Formula –Ex1 • P k=path gain or transmittance of kth forward path. •Δ k= Δ- loop gains that touch the forward path. Ex3-13. Obtain the closed-loop transfer function C(s)/R(s)
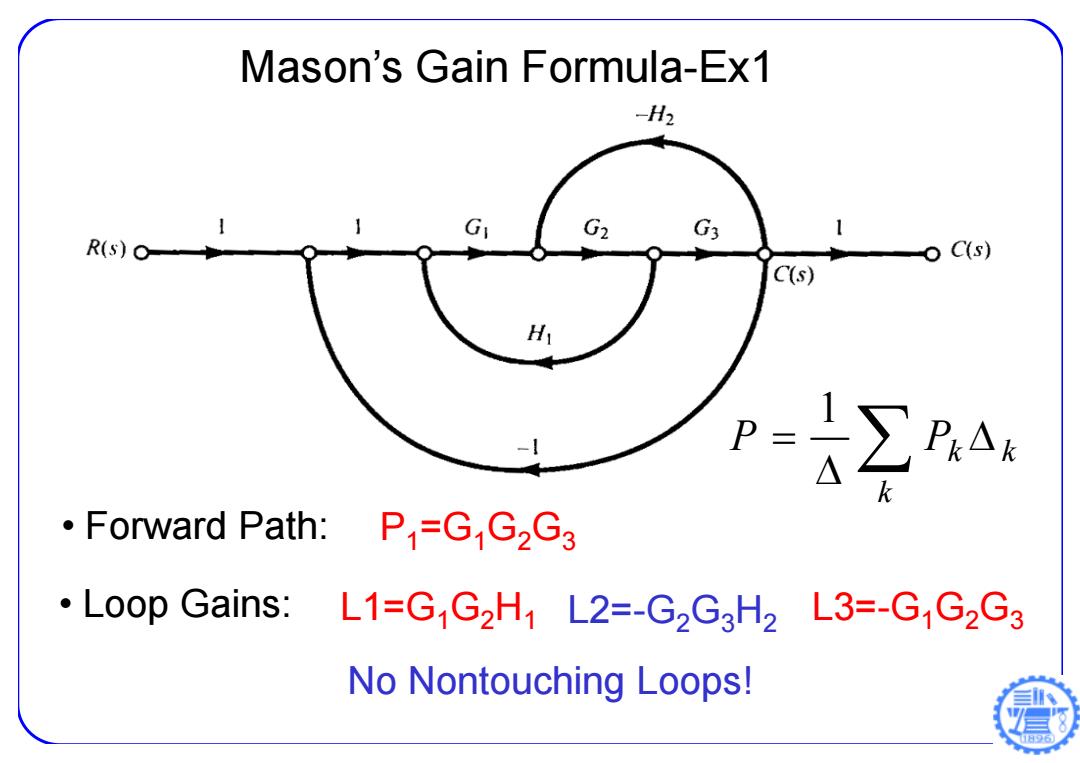
Mason's Gain Formula-Ex1 -H2 G R(s)o C(s) C(s) H P=∑4: Forward Path:P=G G2G3 L00p Gains:L1=GG2H1 L2=-G2G3H2 L3=-GjG2G3 No Nontouching Loops! 日6
Mason’s Gain Formula-Ex1 • Forward Path: P 1=G 1 G 2 G 3 • Loop Gains: L1=G 1 G 2 H 1 L2=-G 2 G 3 H 2 L3=-G 1 G 2 G 3 No Nontouching Loops! k P Pk k 1

Mason's Gain Formula -Ex1 -H2 P1=G1G2G3 L1=G1G2H1 R(s)O一 L2=-G2G3H2L3=-G1G2G3 H A=1-∑La+∑LbL。-∑LabeLy+ b.c de,] 。The determinant△=1-(L1+L2+L3) =1-G1G2H1+G2G3H2+G1G2G3 。The determinant△i =1 A1= GjG2G: R(s) 1-G1G2H1+G2G3H2+G1G2 日96
Mason’s Gain Formula –Ex1 • The determinant Δ= P 1=G 1 G 2 G 3 • The determinant Δ 1 L1=G 1 G 2 H 1 L2=-G 2 G 3 H 2 L3=-G 1 G 2 G 3 1- (L1+L2+L3) =1- G 1 G 2 H 1+ G 2 G 3 H 2+ G 1 G 2 G 3 =1 ( ) ( ) R s C s 1 ... , , , d e f d e f b c b c a L a L L L L L 1 2 1 2 3 2 1 2 3 1 1 1 2 3 1 G G H G G H G G G P G G G k Pk k 1
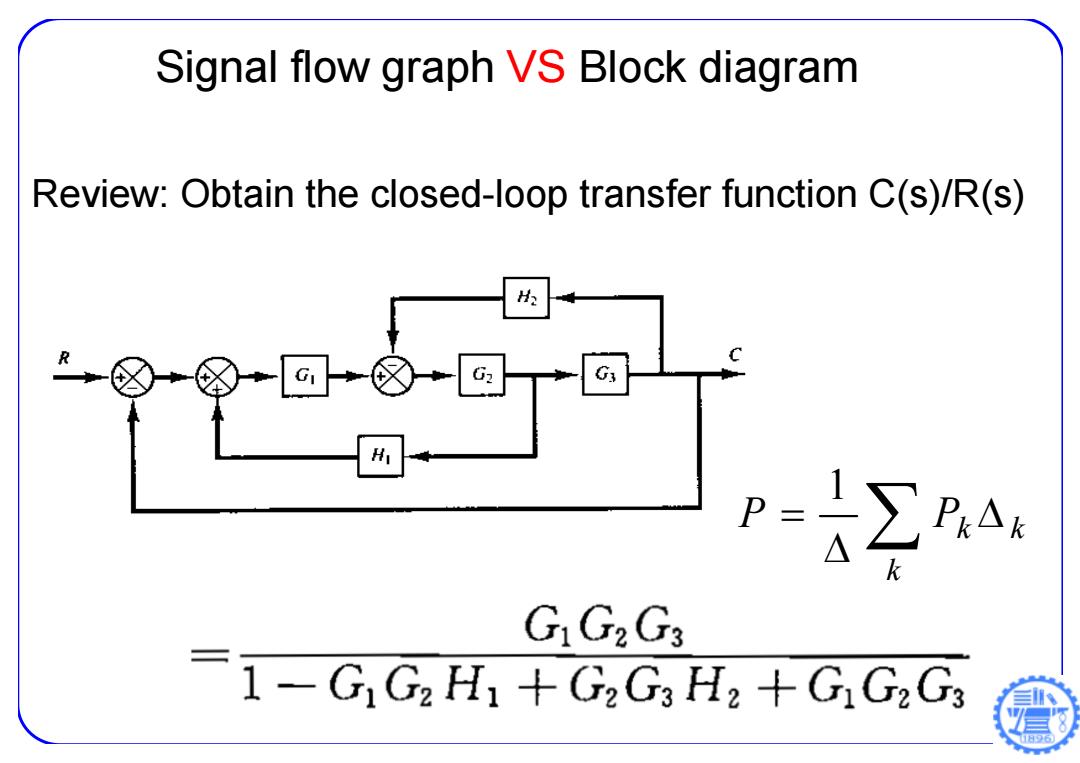
Signal flow graph VS Block diagram Review:Obtain the closed-loop transfer function C(s)/R(s) H k GG2Gs 1-G]G2 H+G2G3 H2+GG2Gs 日96
Signal flow graph VS Block diagram Review: Obtain the closed-loop transfer function C(s)/R(s) k P Pk k 1