
层层 =0.039cm 17牛顿环可有两个曲率半径很大的平凸透镜之间的空气产生(图)。平凸透镜A和B 的曲率半径分别为R1和2?,在波长为600m的单射光垂直照射下观察到第10个暗环半径 F心一4mm.若另有曲率半径为尼的平凸透镜C(图中未画出),并且B、C组合和A、C 组合产生的第10个暗环半径分别为c=45mm和c=5mm,试计算尼、B,和尼,。 解, 2R 同理,c=(R尼 11 元 又对于暗环: 1o=* (3) 题117图 (1X2X3联立并代入数据得:R:=628mB=-4.64mR:=12.4m 18菲涅尔双棱镜实验装置尺寸如下:缝到棱镜的距离为5cm,棱镜到屏的距离为95cm, 棱镜角为α=17932构成棱镜玻璃材料的折射率分=1.5,采用的是单色光。当厚度均匀 的肥皂膜横过双冷静的一半部分放置,该系统中心部分附近的条纹相对原先有0.8mm的位 移。若肥皂膜的折射率为1=1.35,试计算肥皂膜厚度的最小值为多少? 解:如图所示:光源和双棱镜系统的性质相当于相干光源和,它们是虚光源
11 4 15 1 2 39 4 15 1 2 41 0.039cm 17 牛顿环可有两个曲率半径很大的平凸透镜之间的空气产生(图)。平凸透镜 A 和 B 的曲率半径分别为 A 和 ,在波长为 600nm 的单射光垂直照射下观察到第 10 个暗环半径 R RB 。若另有曲率半径为 的平凸透镜 C(图中未画出),并且 B、C 组合和 A、C 4 AB r mm RC 组合产生的第 10 个暗环半径分别为 和 ,试计算 、 和 。 4.5 BC r mm 5 AC r mm RA RB RC 解: 2 2 r h R 2 2 2 1 1 ( ) 2 2 2 1 1 , ( ) 2 1 1 ( ) 2 AB AB AB AB A B A B A B BC BC B C AC AC A C r r r h h h R R R R r h R R r h R R 同理 又对于暗环: 即 2 (2 1) 2 2 h j 2 h j (1) 2 1 1 10 ( ) AB A B r R R (2) 2 1 1 10 ( ) BC B C r R R (3) 2 1 1 10 ( ) AC A B r R R (1)(2)(3)联立并代入数据得: A =6.28m =4.64m =12.4m R RB RC 18 菲涅尔双棱镜实验装置尺寸如下:缝到棱镜的距离为 5cm,棱镜到屏的距离为 95cm, 棱镜角为 构成棱镜玻璃材料的折射率 ,采用的是单色光。当厚度均匀 ' 179 32 ' n 1.5 的肥皂膜横过双冷静的一半部分放置,该系统中心部分附近的条纹相对原先有 0.8mm 的位 移。若肥皂膜的折射率为 n 1.35, 试计算肥皂膜厚度的最小值为多少? 解:如图所示:光源和双棱镜系统的性质相当于相干光源 1 和 ,它们是虚光源。 s 2 s RA RB OA rAB dAB 题 1.17 图

由近似条件8万二D4和日≈(得4=28=2n-)4D 按双棱镜的几何关系得2.1+α=π 所1 2 (2) d 更限入前。相长于的条件为 (3) 4y+(n-l1=n 题1.18图 由于肥皂膜的插入,相长干涉的条件为 (4 1=》_2i-00r-2 由(3)和(4)得 6(n-1) (n-1) 代入数据得1=4.94×10?m 19将焦距为50cm的会聚透镜中央部分C切去(见题图),余下的A、B两部分仍旧料 起来,C的宽度为lcm。在对称轴线上距透镜25cm处置一点光源,发出波长为692nm的红 宝石激光,在对称轴线上透镜的另一侧50cm处置一光屏,平面垂直于轴线。试求: (干涉条纹的间距是多少? (2)光屏上呈现的干涉图样是怎样的? 解 ()透镜由A、B两部分粘合而成,这两部分的主轴都不在该光学系统的中心 A 轴线上,A部分的主轴在中心线上0.5cm处,B部分的主轴在中心线下0.5cm处, 由于单色点光源P经凸透镜A和B所成的像是对称的,故仅需考虑P经B的成 c 像位置即可。 B 111 由5下得5=-50cm B='、s 由因 题1.19图 即所成的虚像在B的主轴下方lcm处,也就是在光学系统对称轴下方0.5cm处,同理,单 色光源经A所成的虚像在光学系统对称轴上方0.5cm处,两虚像构成相干光源,它们之间 的距离为lcm,所以 4=6月6.92x10cm (2)光屏上呈现的干涉条纹是一簇双曲线, 20将焦距为5cm的薄透镜L沿直线方向剂开(见题图)分成两部分A和B,并将A 部分沿主轴右移至2.5cm处,这种类型的装置称为梅斯林对切透镜。若将波长为632.8m的 2
12 由近似条件 和 得 (1) ' ( 1) n A 1 ( ) 2 d l ' d l l n A 2 2 ( 1) 按双棱镜的几何关系得 2A 所以 (2) ' 14 2 A 肥皂膜插入前,相长干涉的条件为 (3) 0 d y j r 由于肥皂膜的插入,相长干涉的条件为 (4) ' 0 ( 1) d y n t j r 由(3)和 (4)得 ' ' ' 0 0 ( ) 2 ( 1) ( ) ( 1) ( 1) d y y l n A y y t r n r n 代入数据得 7 t m 4.94 10 19 将焦距为 50cm 的会聚透镜中央部分 C 切去(见题图),余下的 A、B 两部分仍旧粘 起来,C 的宽度为 1cm。在对称轴线上距透镜 25cm 处置一点光源,发出波长为 692nm 的红 宝石激光,在对称轴线上透镜的另一侧 50cm 处置一光屏,平面垂直于轴线。试求: (1)干涉条纹的间距是多少? (2)光屏上呈现的干涉图样是怎样的? 解: (1) 透镜由 A、B 两部分粘合而成,这两部分的主轴都不在该光学系统的中心 轴线上,A 部分的主轴在中心线上 0.5cm 处,B 部分的主轴在中心线下 0.5cm 处, 由于单色点光源 P 经凸透镜 A 和 B 所成的像是对称的,故仅需考虑 P 经 B 的成 像位置即可。 由 得 1 1 1 s s f ' ' s cm ' 50 由因为 所以 y s ' ' y s ' ' 1 s y y cm s 即所成的虚像在 B 的主轴下方 1cm 处,也就是在光学系统对称轴下方 0.5cm 处,同理,单 色光源经 A 所成的虚像在光学系统对称轴上方 0.5cm 处,两虚像构成相干光源,它们之间 的距离为 1cm,所以 3 0 y r cm 6.92 10 d (2)光屏上呈现的干涉条纹是一簇双曲线。 20 将焦距为 5cm 的薄透镜 L 沿直线方向剖开(见题图)分成两部分 A 和 B,并将 A 部分沿主轴右移至 2.5cm 处,这种类型的装置称为梅斯林对切透镜。若将波长为 632.8nm 的 S S1 S2 d θ α A1 l1 n’ (a) y · · · · d S1 S2 r 0 n (b) 题 1.18 图 A B C 题 1.19 图

点光源P置于主轴上离透镜Lg距离为10cm处,试分析:()成像情况如何?(2)若在Lg右 边10.5cm处置一光屏,则在光屏上观察到的干涉图样如何? 解:(1)如图(b)所示,该情况可以看作由两个挡掉 半的透镜L和LB构成,其对称轴为 PO,但是主轴和光心却发生了平移.对于透镜L其光心移到0处,而主轴上移0.01cm到 OFx:对于透镜Lg,其光心移到Oe处,而主轴下移0.01cm到OFg点光源P恰恰在透镜的对称 轴上二倍焦距处由于物距和透镜L、LB的焦距都不变,故通过LA、LB成像的像距也不变。 根据物像公式 11=1 N pp f 将p=-10cm和/=5cm代水上式,得 p=5cm B=2 B -D- y-0.01cm 由于P点位于透锭L的光轴下方OO1c按透镜的成像实像P,应在透镜L, 主轴上方0.01cm处:同理,P点位于透镜LB主轴上方0.01cm处,实像Pa应在主轴下方0.01 cm处. 两像点的距离为上方0.01cm处 PaPu-d=21 0.04cm (2)由于实像P和P构成了一对相干光源,而且相干光束在观察屏的区域上是相互交叠的, 故两束光叠加后将发生光的干涉现象屏上呈现干涉花样按杨氏干涉规律两相邻亮条纹的 间距公式为 A=6号 将数据代入得△y=1.582mm 21 如图所示,A为平凸透镜,B为平玻璃板,C为金属柱,D为框架,A、B间有空 隙,图中绘出的是接触的情况,而A固结在框架的边缘上。温度变化时,C发生伸缩,而 假设A、B、D都不发生伸缩。以波长632.8nm的激光垂直照射。试问: (I)在反射光中观察时,看到牛顿环条纹移向中央,这表示金属柱C的长度在增加还是减小? (2)若观察到有10个亮条纹移向中央而消失,试问C的长度变化了对少毫米? 解:(1)因为在反射光中观察牛顿环的亮条纹, 2U=12,3.) 2 6=2h-1/2=
13 A B P LA LB • 题 1.20 图 点光源 P 置于主轴上离透镜 LB 距离为 10cm 处,试分析:(1) 成像情况如何?(2)若在 LB右 边 10.5cm 处置一光屏,则在光屏上观察到的干涉图样如何? 解 :( 1)如图(b)所示,该情况可以看作由两个挡掉一半的透镜 LA 和 LB 构成,其对称轴为 PO,但是主轴和光心却发生了平移.对于透镜 LA,其光心移到 OA 处,而主轴上移 0.01cm 到 OAFA;对于透镜 LB,其光心移到 OB处,而主轴下移 0.01cm到 OBFB.点光源 P 恰恰在透镜的对称 轴上二倍焦距处.由于物距和透镜 LA、LB的焦距都不变,故通过 LA 、LB成像的像距也不变。 根据物像公式 将 p=-10cm 和 =5cm 代入上式,得 ' f =5cm ' p = =-1 y ' y ' p p 故 =-0.01 cm ' y 由于 P 点位于透镜 LA的光轴下方 0.01 cm,按透镜的成像规律可知,实像 PA 应在透镜 LA 主轴上方 0.01 cm 处;同理,P 点位于透镜 LB主轴上方 0.01 cm 处, 实像 PB应在主轴下方 0.01 cm 处. 两像点的距离为上方 0.01 cm 处. PAPB=d=2| |+ ' y h =0.04cm (2)由于实像 PA 和 PB 构成了一对相干光源,而且相干光束在观察屏的区域上是相互交叠的, 故两束光叠加后将发生光的干涉现象,屏上呈现干涉花样.按杨氏干涉规律,两相邻亮条纹的 间距公式为 0 y r d 将数据代入得 =1.582mm y 21 如图所示,A 为平凸透镜,B 为平玻璃板,C 为金属柱,D 为框架,A、B 间有空 隙,图中绘出的是接触的情况,而 A 固结在框架的边缘上。温度变化时,C 发生伸缩,而 假设 A、B、D 都不发生伸缩。以波长 632.8nm 的激光垂直照射。试问: (1)在反射光中观察时,看到牛顿环条纹移向中央,这表示金属柱 C 的长度在增加还是减小? (2)若观察到有 10 个亮条纹移向中央而消失,试问 C 的长度变化了对少毫米? 解 :( 1)因为:在反射光中观察牛顿环的亮条纹, 2 2 / 2 ( 1, 2,3,.) 2 r h j j R 及干涉级 j 随着厚度 h 的增加而增大,即随着薄 膜厚度的增加,任意一个指定的 j 级条纹将缩小 ' ' 1 1 1 p p f
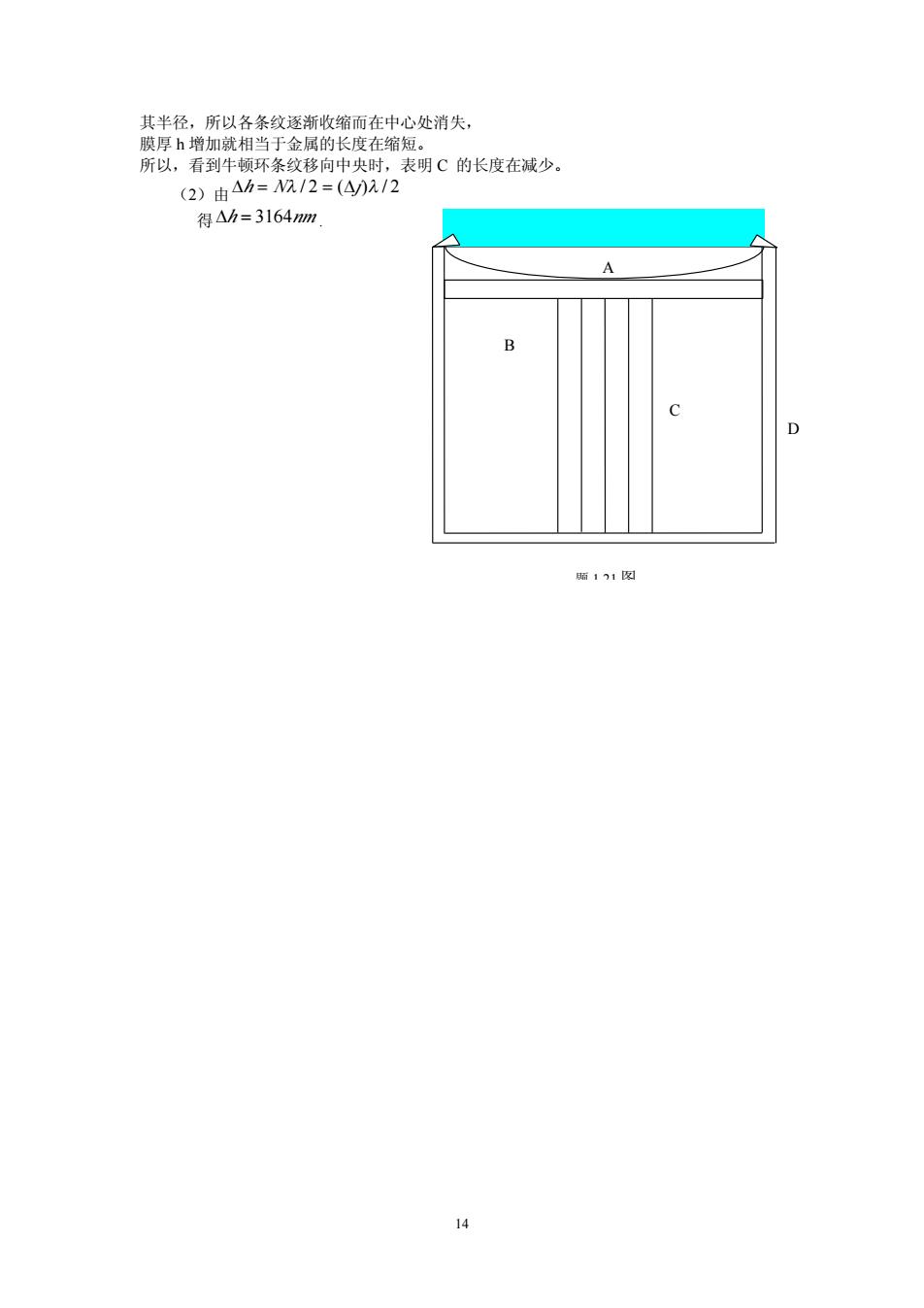
其半径,所以各条纹逐渐收缩而在中心处消失, 膜厚h增加就相当于金属的长度在缩短。 所以,看到牛顿环条纹移向中央时,表明C的长度在减少。 (2)由△h=M/2=(④)2/2 得△h=3164m A 增111网
14 其半径,所以各条纹逐渐收缩而在中心处消失, 膜厚 h 增加就相当于金属的长度在缩短。 所以,看到牛顿环条纹移向中央时,表明 C 的长度在减少。 (2)由 h N / 2 (j) / 2 得 h nm 3164 . C B A D 题 1.21 图

第二章光的衍射 1.单色平面光照射到一小圆孔上,将其波面分成半波带。求第K个带的半径。若极点到 观察点的距离ro为1m,单色光波长为450m,求此时第一半波带的半径。 解分=pi+公雨e6+分 方-格 +石-=经 将上式两边平方,得 +分=公+元+恐 4 略去项,则P:=习 将k=16=100cm,2=450x10*cm带入上式,得 p=0.067cm 2.平行单色光从左向右垂直射到一个有圆形小孔的屏上,设此孔可以像照相机光圈那样 改变大小。问:(1)小孔半径满足什么条件时,才能使得此小孔右侧轴线上距小空孔中心 4的P点的光强分别得到极大值和极小值:(2)P点最亮时,小孔直径应为多大?设此时的 波长为500m 解:(1)根据上题结论P=VP 将6=400cm,元=5x10cm代入,得 p4=V400×5×10-k=0.1414Wcm 当k为奇数时,P点为极大值: k为偶数时,P点为极小值。 (2)P点最亮时,小孔的直径为 2p,=2V61=0.2828cm 3.波长为500m的单色点光源离光阑1n,光阑上有一个内外半径分别为0.5m和1m 的透光圆环,接收点P离光阑1m,求P点的光强I与没有光阑时的光强度1之比。 解:根据题意 R=Im=Im R,=0.5mm R,1mm =500nm 有光阑时,由公式
15 第二章 光的衍射 1. 单色平面光照射到一小圆孔上,将其波面分成半波带。求第к个带的半径。若极点到 观察点的距离 r0为 1m,单色光波长为 450nm,求此时第一半波带的半径。 解: 而 2 0 2 2 r r k k 2 0 r r k k 2 0 k r r k 2 0 2 0 2 k r r k 将上式两边平方,得 4 2 2 0 2 0 2 0 2 k r r kr k 略去 项,则 2 2 k k kr 0 将 带入上式,得 1, 100cm, 4500 10 cm -8 k r 0 0.067cm 2. 平行单色光从左向右垂直射到一个有圆形小孔的屏上,设此孔可以像照相机光圈那样 改变大小。问:(1)小孔半径满足什么条件时,才能使得此小孔右侧轴线上距小空孔中心 4m 的 P 点的光强分别得到极大值和极小值;(2)P 点最亮时,小孔直径应为多大?设此时的 波长为 500nm。 解 :( 1)根据上题结论 k kr 0 将 代入,得 400cm, 5 10 cm -5 r 0 400 5 10 0.1414 cm 5 k k k 当 k 为奇数时,P 点为极大值; k 为偶数时,P 点为极小值。 (2)P 点最亮时,小孔的直径为 21 2 r 0 0.2828cm 3.波长为 500nm 的单色点光源离光阑 1m,光阑上有一个内外半径分别为 0.5mm 和 1mm 的透光圆环,接收点 P 离光阑 1m,求 P 点的光强 I 与没有光阑时的光强度 I0之比。 解:根据题意 R 1m 1m R 0.5mm R 1mm 500nm 0 hk1 hk2 r 有光阑时,由公式 r R R r R R R r k h ( ) h 1 1 0 2 0 0 2