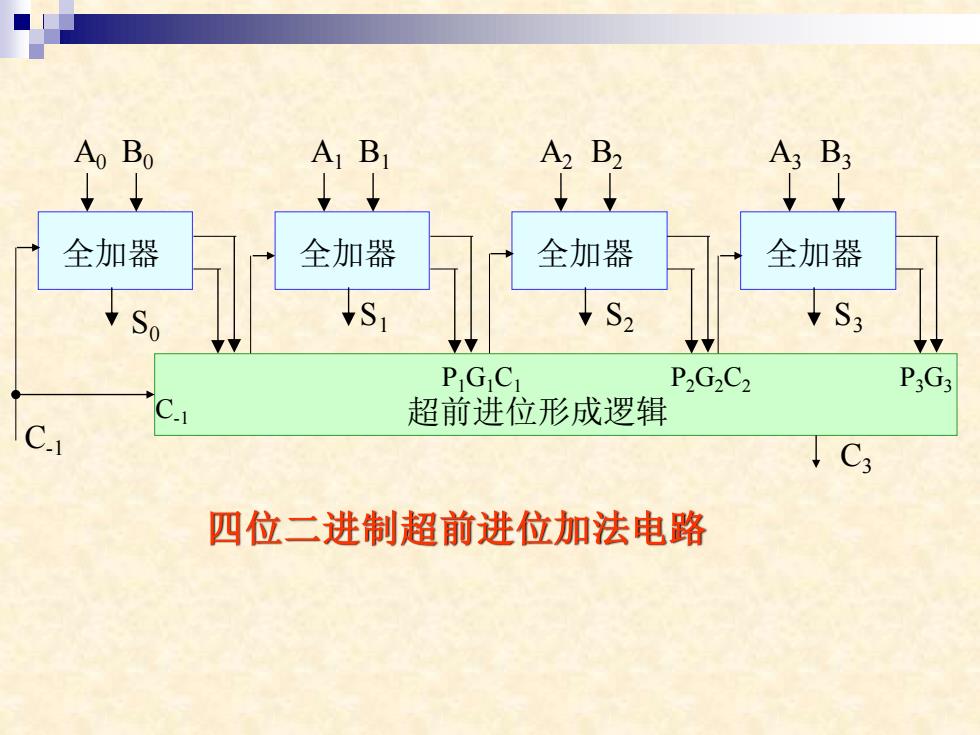
Ao Bo A1 B A2 B2 A3 B3 ↓↓ , g9 全加器 全加器 全加器 全加器 So S S2 1S3 PGjCi P2G2C2 P:G3 C.1 超前进位形成逻辑 C ↓C3 四位二进制超前进位加法电路
四位二进制超前进位加法电路 P0G0C0 S S1 S2 S3 0 A0 B0 A1 B1 A2 B2 A3 B3 全加器 全加器 全加器 全加器 C-1 超前进位形成逻辑 P1G1C1 P2G2C2 P3G3 C-1 C3
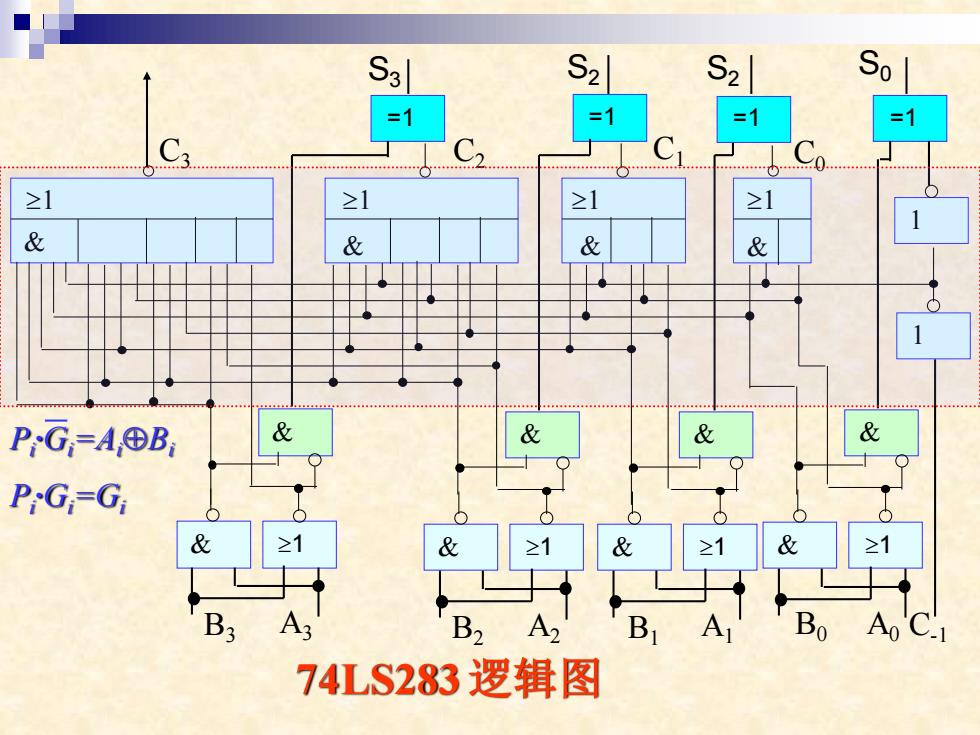
S2S2 So =1 =1 =1 =1 ≥1 & & & PG=A⊕B, & P:G=G 年过 74LS283逻辑图
74LS283 逻辑图 & 1 1 & 1 & 1 & C3 C-1 C0 C2 C1 B3 A3 =1 1 1 & 1 & =1 =1 =1 B1 A1 & 1 & B2 A2 & 1 & B0 A0 & 1 & S3 S2 S2 S0 Pi ∙Gi=AiBi Pi ∙Gi=Gi

例:用四位二进制并行加法器设计一个将 8421BCD码转换成余3码的代转换电路。 解:余3码比8421码多3 余3码 F4 F3 F2 F1 FC4 Co 0” A4 A3 A2 A B4 B3 B2 B1 8421BCD码0011
例: 用四位二进制并行加法器设计一个将 8421BCD码转换成余3码的代转换电路。 余3码比8421码多3 A4 A3 A2 A1 B4 B3 B2 B1 F4 F3 F2 F1 余3码 FC4 C0 8421BCD码 0 0 1 1 “ 0” 解:

例:用四位二进制并行加法器设计一个 四位二进制并行加法/减法器。 解:利用补码,将减法变为加法
例: 用四位二进制并行加法器设计一个 四位二进制并行加法/减法器。 解: 利用补码,将减法变为加法
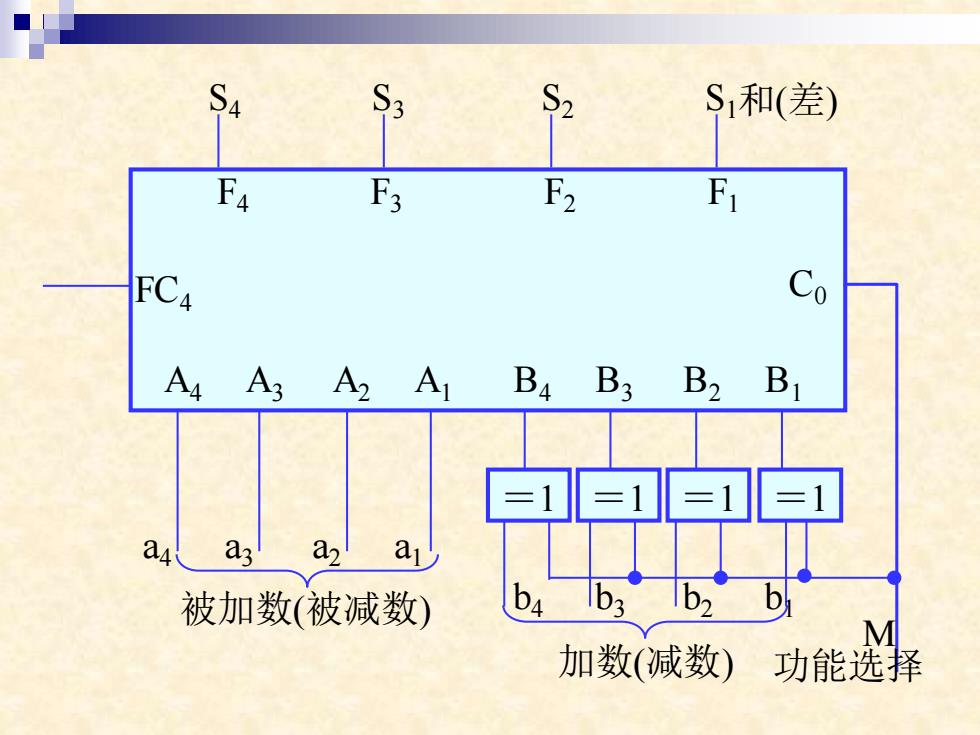
S4 S3 S2 S1和(差) F4 F3 F2 F FC4 Co A4 A3 A2 A Ba B3 B2 B 1=1 a a a 被加数(被减数) ba b3 b2 b M 加数(减数)功能选择
F4 F3 F2 F1 FC4 C0 A4 A3 A2 A1 B4 B3 B2 B1 S4 S3 S2 S1 =1 =1 =1 =1 被加数(被减数) 加数(减数) a4 a3 a2 a1 b4 b3 b2 b1 功能选择 M 和(差)