
Entropy of Mixing (1) S.J.T.U. Phase Transformation and Applications To calculate the entropy of mixing of two ideal gases. One gas expands isothermally from V to Vr in the apparatus shown schematically below. nR VT ideal gas Initially ds-nkdvn rdiny evacuated S2-S,=nRInV H U SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (1) dV n Rd V V nR dS T a T a V V V V S S ln 2 1 = = To calculate the entropy of mixing of two ideal gases. ideal gas V nR T P V S T V = = Va VT Initially evacuated One gas expands isothermally from Va to VT in the apparatus shown schematically below. a T V V S2 − S1 = nRln

Entropy of Mixing (2) S.J.T.U. Phase Transformation and Applications To calculate the entropy of mixing of two ideal gases. Because ideal gases do not interact,we can calculate the total entropy change as the sum of the two entropy changes of the individual gases. (S-S)。=,RIn'g+么 Va Va Va 2-S=nS2-S,。+m,S,-S。=%,Rn'aa+m,Rn Per mole of mixture: S-S=”Rn。 +业+ nbRnVb Va+Vo na+np na+np n+np H SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (2) To calculate the entropy of mixing of two ideal gases. Because ideal gases do not interact, we can calculate the total entropy change as the sum of the two entropy changes of the individual gases. ( ) a a b a a V V V S S n R + 2 − 1 = ln Va VT Vb ( ) ( ) b a b b a a b a a b b a V V V n R V V V S S n S S n S S n R + + + 2 − 1 = 2 − 1 + 2 − 1 = ln ln Per mole of mixture: b a b a b b a a b a b a a b V V V R n n n V V V R n n n n n S S + + + + + = + − ln ln 2 1
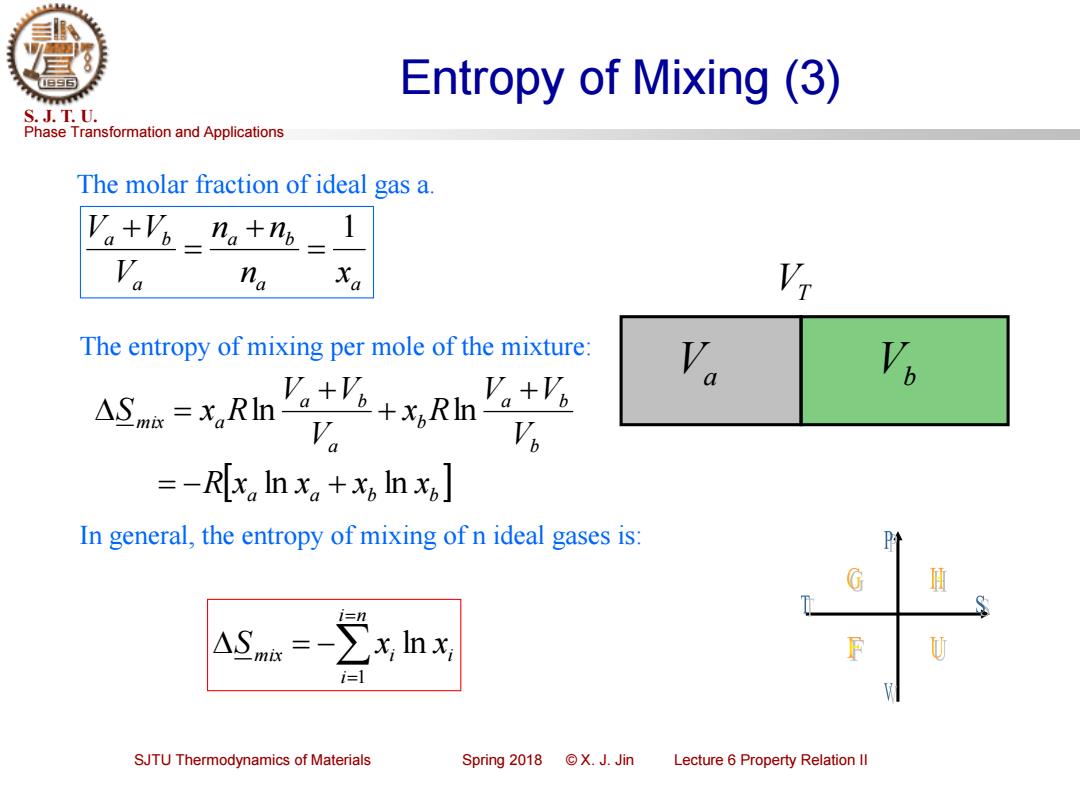
Entropy of Mixing (3) S.J.T.U. Phase Transformation and Applications The molar fraction of ideal gas a. V。+'a-n。+n=1 na Xa The entropy of mixing per mole of the mixture: Va Va AS.-s,ki V =-R[x Inx。+x,lnx] In general,the entropy of mixing of n ideal gases is: i=1 SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (3) The molar fraction of ideal gas a. Va VT a a a b a a b n x n n V V V 1 = + = + Vb a a b b b a b b a a b mix a R x x x x V V V x R V V V S x R ln ln ln ln = − + + + + = In general, the entropy of mixing of n ideal gases is: The entropy of mixing per mole of the mixture: = = = − i n i mix i i S x x 1 ln

On Gibbs free energy S.J.T.U. Phase Transformation and Applications -lw=-oW +oW actual Slw T T &Q=dUU-δW dS≥ T 2=dU+p外dV-oW' TdS-du-pndV-W 有效功 SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il
Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II On Gibbs free energy −lw= −Wrev +W T lw T Q dS actual = − T Q dS actual Q = dU + p 外dV −W' TdS −dU − p 外dV −W' Q = dU −W 有效功