
Nanjing University 金属的介电函数 OP 根据方程: D=8E+P,J= 8t 得到金属的介电函数,(金属对外电场的响应) 8(K,o)=1+ io(K,@) 800 02D 再由波动方程 VxV×E=-4oat2 K2=(K,0)0 Generic dispersion relation Dielectric Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University 根据方程: 0 ε , ∂ = + = P 根据方程: D EP J 得到金属的介电函数,(金属对外电场的响应) 0 , t ε + ∂ D EP J 0 (,) (,)1 iσ ω ε ω ε ω = + K K 0 再由波动方程 2 0 2 t μ ∂ ∇×∇× = − ∂ D E 2 2 2 K (,) c ω = ε ω K Generic dispersion relation Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn

Nanjing University 内容纲要 背景 >体等离激元 基本原理 >表面等离激元 物理效应 >局域等离激元 相关应用 Dielectrie Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University 背景 基本原理 ¾体等离激元离 物理效应 ¾表面等离激元 ¾局域等离激元 相关应用 Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn
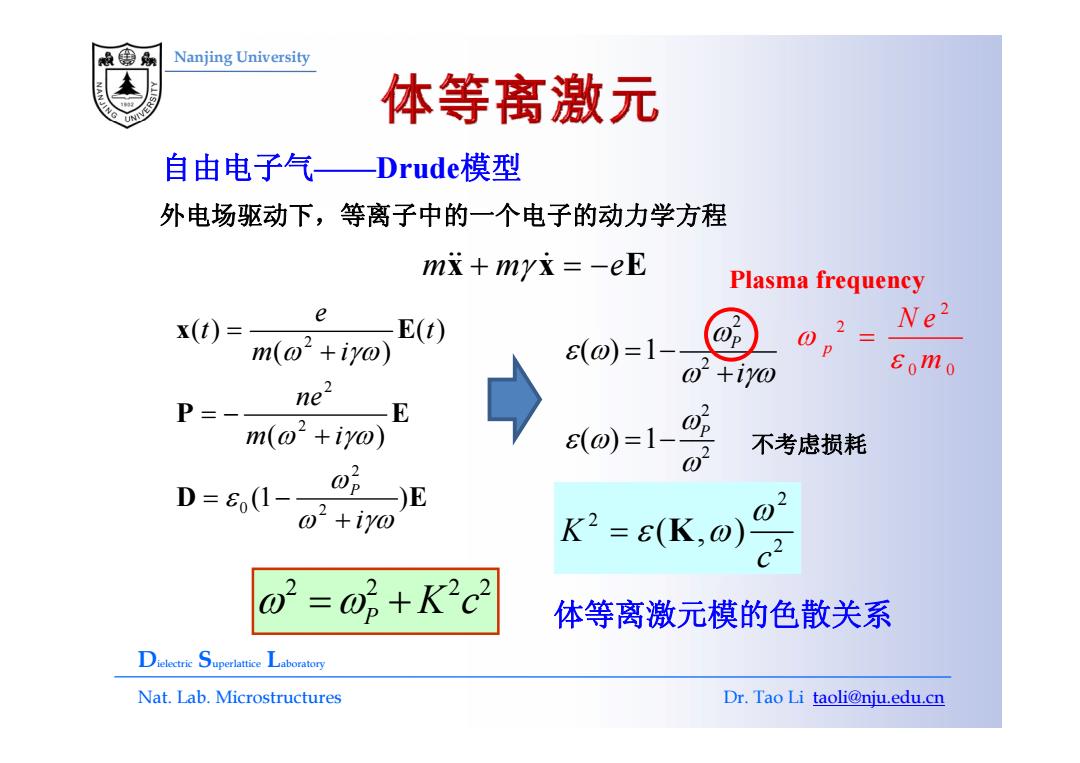
Nanjing University 体等离激元 自由电子气—Drude模型 外电场驱动下,等离子中的一个电子的动力学方程 mx+myx=-eE Plasma frequency x()= E(t) 2 Ne2 m(a+iyo) (0)=1- o +iyo Eomo ne2 P=- —E m(o2+iy@) o)=1-g 不考虑损耗 D=6(1- )E @2+iy@ K2=6(K,o)2 o2=06+K2c2 体等离激元模的色散关系 Dielectric Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University 自由电子气——Drude模型 外电场驱动下 等离子中的 个电子的动力学方程 mm e && & x xE + γ = − 外电场驱动下,等离子中的一个电子的动力学方程 Plasma frequency 2 2 () () ( ) e t t m i ω γω = + x E 2 2 () 1 Pi ω ε ω ω γω = − + 2 2 0 0 p N em ω ε = 2 2 2 ( ) ne m i ω γω = − + P E 2 2 () 1 P ω γωi ω ε ω ω + = − 不考虑损耗 2 0 2 (1 ) Pi ω ε ω γω = − + D E ω 2 2 2 K (,) c ω = ε ω K 2 2 22 ω ω= +P K c 体等离激元模的色散关系 c Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn
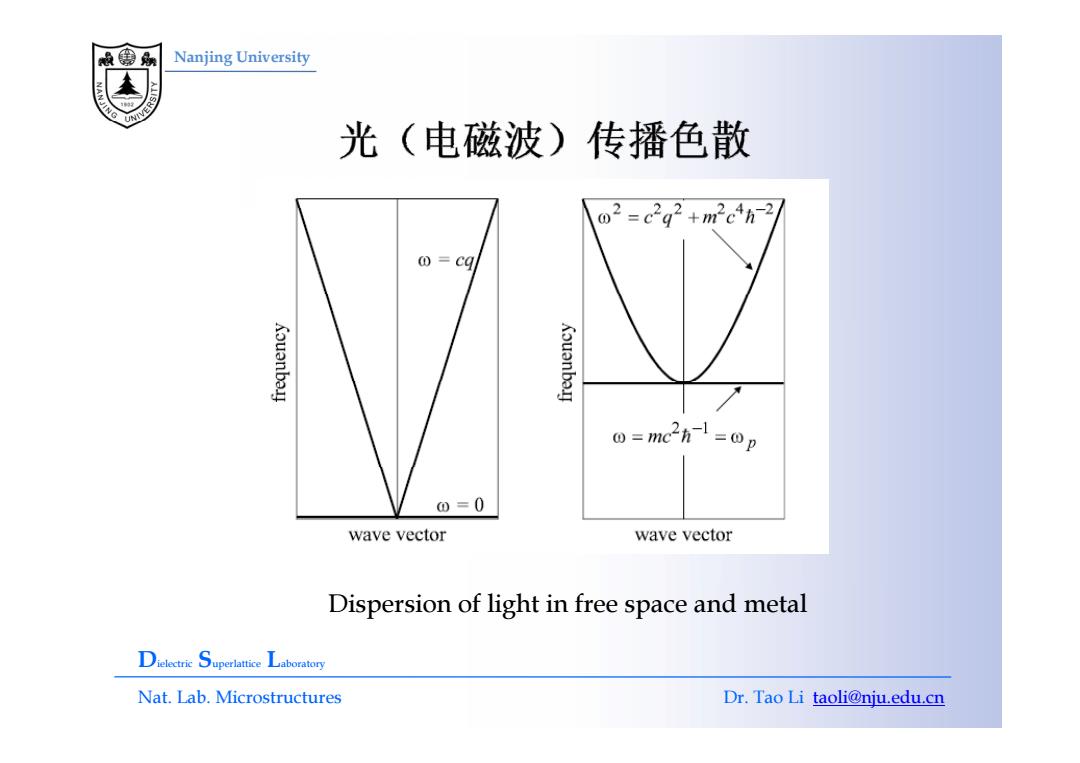
版象 Nanjing University 光(电磁波)传播色散 02=c2g2+m2c4h2 ①=cg Kouanbay Kouanba.y 0=mc2h1=0p 0=0 wave vector wave vector Dispersion of light in free space and metal Dielectrie Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University Dispersion of light in free space and metal Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn

Nanjing University Lorentz模型(谐振子) 考虑到有些情况的电子并非完全自由,而是受到各种各样的约束, 如材料结构的几何形状,结构边界,电子的带间跃迁等等,这些约 束可以用回复力mox表示,因而,动力学方程变为: mx+myx+moox =-eE (⊙)=1+ 0-02-iy0 Lorentz模型 一般描述共振系统 Dielectric Superlattice Laboratory Nat.Lab.Microstructures Dr.Tao Li taoli@nju.edu.cn
Nanjing University Lorentz模型(谐振子) 考虑到有些情况的电子并非完全自由,而是受到各种各样的约束, 如材料结构的几何形状,结构边界,电子的带间跃迁等等,这些约 束可以用回复力mω0x表示,因而,动力学方程变为: mm m e 0 && & x x xE + + γ ω = − 0 mm m e 0 x x xE + + γ ω 2 () 1 ωP ε ω = + 2 2 0 () 1 i ε ω ω ω γω = + − − Lorentz 模型 一般描述共振系统 Dielectric Superlattice Laboratory Nat. Lab. Microstructures Dr. Tao Li taoli@nju.edu.cn