上海交通大学：《飞机设计 Aircraft Design》课程教学资源_Aircraft Design - 19-Multidisciplinary Design Analysis and Optimization

5/16/2018 国上清庆大坐 Overview of Lectures 国上清大学 0.Overview 14/15 Performance(a,b) 16.Aircraft certification 2.Overall configuration 17.Aviation economics weight estimation 18.System integration and estimation configuration management Aircraft Design Fuselage design 19.Multidisciplinary design 6/7/8 Aerodynamic design(a,b,c) ootimization (飞行器设计) .hat and ing 20.Military aircraft design-overview 21.Environmental issues 10.Landing gear and Aircraft systems 22.Design skills 11.Power plant Wenbin Song 12.Stability and control School of Aeronautics and Astronautics 13.Loads,materials and structures oorornenin ong Overview 国上活美大坐 Objectives 国上清大坐 Objectives and introduction to optimization Basic background knowledge on numerical optimizations Basic procedures in optimization -Optimization aloorithms Optimization methods -Problem formulation Single variable methods -Solution methods and strateaies -Multivariable methods Engineering application of optimization -Handling of constraints -Application of basic algorithms in simple engineering design problems -Multi-objective optimization Complex optimization problem solving using combination of algorithms Engineering optimization using CAD/FEM/CFD -Aircraft conceptual design using multidisciplinary design optimization Multidisciplinary analysis and optimization (MDO) Aircraft design using MDO rrogate modeling -Robust design -HPC,Grid Computing and beyond oerandenn ong Introduction to Optimization 图上洋大峰 General Framework 国上洋大学 An optimization problem can be defined as Computational simulations becomes increasingly accurate (and computationl demanding) Minimize f(x).i=1.....P. Coupled with parametric modeling and numerical optimization subject to gi(x刘≥0.j=1..人 0 methods proved valuable in design innovation and improvements hs(x)=0,k=1.·,K where xis a vector containingn design variables,and P.J and K are the Grid Generation number of objectives,inequality and equality constraints.respectively An example optimization problem definition Optimization t Algorithms ssing Aidfoil optimization (1)Representation of airfoils nulation-based Design Optimizatior 月，≥a.12-thicknessconstraint rslty-Dr.V(enbin Song 1

5/16/2018 1 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Wenbin Song School of Aeronautics and Astronautics Shanghai Jiao Tong University swb@sjtu.edu.cn Aircraft Design （飞行器设计） © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Overview of Lectures 0. Overview 1. Introduction 2. Overall configuration 3. Preliminary weight estimation 4. Refined weight estimation 5. Fuselage design 6/7/8 Aerodynamic design(a, b, c) 9. Thrust/Weight ratio and wing loading 10.Landing gear and Aircraft systems 11.Power plant 12.Stability and control 13.Loads, materials and structures 14/15 Performance(a, b) 16.Aircraft certification 17.Aviation economics 18.System integration and configuration management 19.Multidisciplinary design optimization 20.Military aircraft design – overview 21.Environmental issues 22.Design skills © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Overview • Objectives and introduction to optimization • Basic procedures in optimization • Optimization methods – Single variable methods – Multivariable methods – Handling of constraints – Multi-objective optimization • Engineering optimization using CAD/FEM/CFD • Multidisciplinary analysis and optimization (MDO) • Aircraft design using MDO • Advanced topics – Surrogate modeling – Robust design – HPC, Grid Computing and beyond 3 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Objectives • Basic background knowledge on numerical optimizations – Optimization algorithms – Problem formulation – Solution methods and strategies • Engineering application of optimization – Application of basic algorithms in simple engineering design problems – Complex optimization problem solving using combination of algorithms – Aircraft conceptual design using multidisciplinary design optimization 4 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Introduction to Optimization • An optimization problem can be defined as 5 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics General Framework • Computational simulations becomes increasingly accurate (and computational demanding) • Coupled with parametric modeling and numerical optimization methods proved valuable in design innovation and improvements 6 Parametric Models Grid Generation CFD Analysis Structural Analysis etc. Post- Processing Optimization Algorithms Geometry Grid File Flow data Objective Functions Design Variables Simulation-based Design Optimization Results

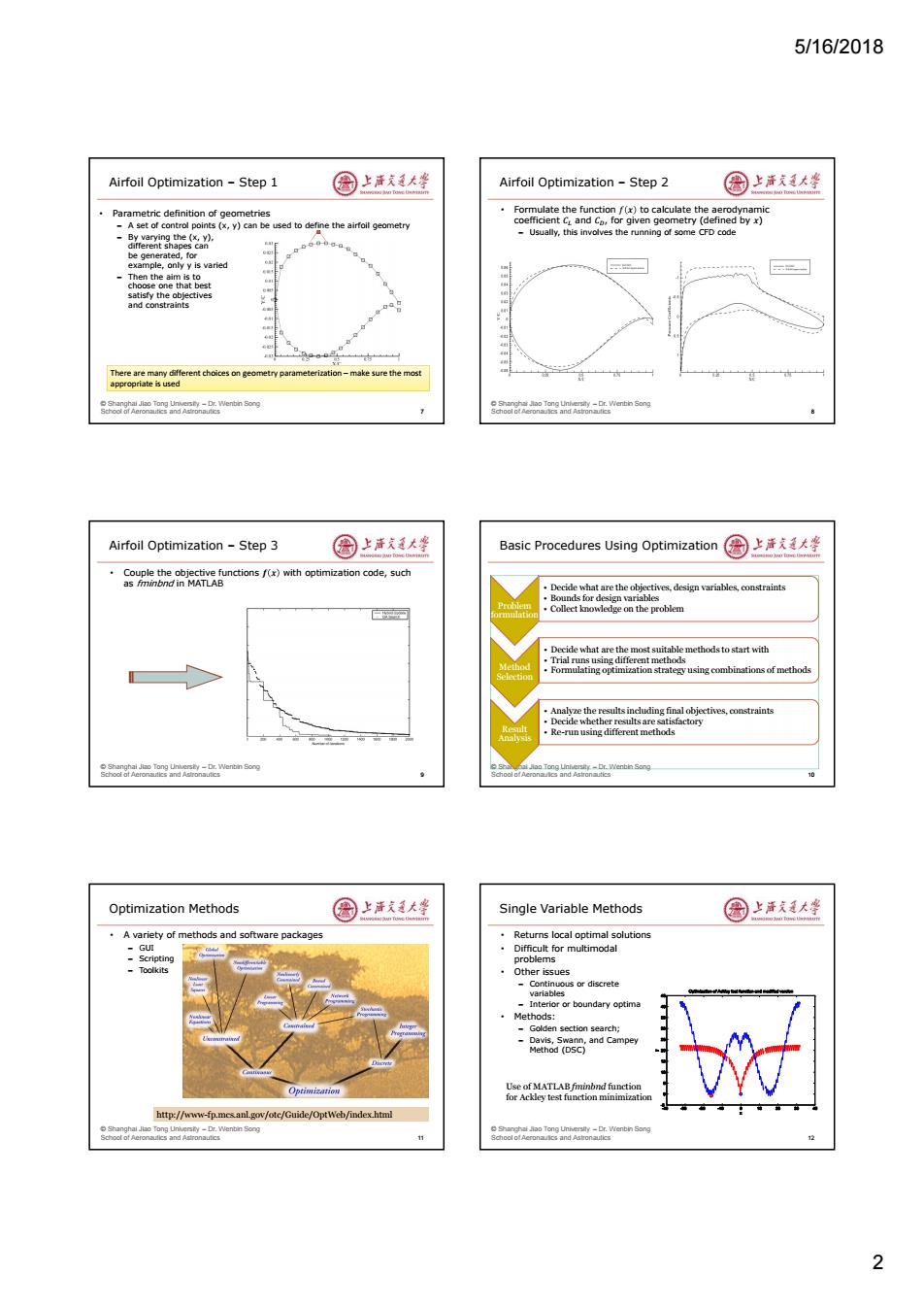
5/16/2018 Airfoil Optimization-Step 1 园上声克大学 Airfoil Optimization -Step 2 国上清大学 Parametric definition of geometries Formulate the function f(x)to calculate the aerodynamic -A set of control points (x,y)can be used to define the airfoil geometry coefficient Cr and Co,for given geometry (defined by x) -Usually,this involves the running of some CFD code E Then the aim is to ◆ t satisfy the objectives and constraints There are mam different choices on ce tation-make sure the mos appropriate is used Airfoil Optimization Step 3 圈上活大坐 Basic Procedures Using Optimization 园上活道大整 Couple the objective functions f(x)with optimization code,such as fminbnd in MATLAB ctk edge on the problem Decide what are the most suitable methods to start with Trial runs using different methods Formulating optimization strategy using combinations of methods Analyze the results including final objectives,constraints Decide whether results are satisfactory Re-run using different methods Optimization Methods 圈上洋文大学 Single Variable Methods 园上海发大坐 A variety of methods and software packages Returns local optimal solutions GUI Difficult for multimodal Scripting problems -Toolkits ·Other issues -Continuous or discrete variables Interior or boundary optima 。Methods n section search; and Camp9 Optimization Use of MATLAB fmminbnd function for Ackley test function minimization http://www-fp.mcs.anL.gov/otc/Guide/OptWeb/index.html Shanghal Jlao Tong Unkersty-Dr.Wenbin Song rslty-Dr.V(enbin Song 2

5/16/2018 2 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Airfoil Optimization – Step 1 • Parametric definition of geometries – A set of control points (x, y) can be used to define the airfoil geometry – By varying the (x, y), different shapes can be generated, for example, only y is varied – Then the aim is to choose one that best satisfy the objectives and constraints 7 There are many different choices on geometry parameterization – make sure the most appropriate is used © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Airfoil Optimization – Step 2 8 • Formulate the function 𝑓 𝒙 to calculate the aerodynamic coefficient 𝐶௅ and 𝐶஽, for given geometry (defined by 𝒙) – Usually, this involves the running of some CFD code © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Airfoil Optimization – Step 3 9 • Couple the objective functions 𝒇 𝒙 with optimization code, such as fminbnd in MATLAB © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Basic Procedures Using Optimization 10 Problem formulation • Decide what are the objectives, design variables, constraints • Bounds for design variables • Collect knowledge on the problem Method Selection • Decide what are the most suitable methods to start with • Trial runs using different methods • Formulating optimization strategy using combinations of methods Result Analysis • Analyze the results including final objectives, constraints • Decide whether results are satisfactory • Re-run using different methods © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Optimization Methods • A variety of methods and software packages – GUI – Scripting – Toolkits 11 http://www-fp.mcs.anl.gov/otc/Guide/OptWeb/index.html © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Single Variable Methods • Returns local optimal solutions • Difficult for multimodal problems • Other issues – Continuous or discrete variables – Interior or boundary optima • Methods: – Golden section search; – Davis, Swann, and Campey Method (DSC) 12 Use of MATLAB fminbnd function for Ackley test function minimization

5/16/2018 Multivariable Methods 圆上活大学 Evolutionary Methods 国上清大学 Sinale-variable methods can be extended into multiple variables. Population-based methods,inspired by biological evolution: and often used as a tool in multivariable methods to find direction reproduction,mutation, of the search(line search) Ior near-global solutions, Multivariable methods espec nctions -Quasi-Newton But suffers one big problem: -DFP (Davidon,Fletcher and Powell) slow and premature convergence 。Solutions: -Direct Search -Hybrid with other efficient -Hill Climbing gradient-based methods oorn enin Song Handling of Constraints 圆上活文大些 Dealing with Multiple Objectives(I) 圈上活大整 Eliminate as many constraints as possible using constraint The first type of approach is based on weighted sum method analysis 。 Use of peatwhichmfd bjtve function considering the extent to which the constra- Up=U6)+r∑h+r∑Kg,》 e if 30 吻=∑wf 0fg>0 Multi-objective approach optimization process. -Use of multi-objective optimization approach by treating each constraint as an objective function oerandenn ong Dealing with Multiple Objectives(II) 圆上洋道大坐 Dealing with Multiple Objectives()上ǐi大Y The second type of approach is based on multi-objective methods Methods to obtain Prato-front Pareto front optimization weighted methods,by varying the weight coefficients ev Definition 1.Vector f(x)s f(x).ff(x)f)=1...P and 之 nx(x Strength Pareto GA (SPGA) Definition 2.Solndion x dominates)f). 0 NSGA-II。 0.8 0 N0.6 04 02 rslty-Dr.V(enbin Song 0g0204,96081 3

5/16/2018 3 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Multivariable Methods • Single-variable methods can be extended into multiple variables, and often used as a tool in multivariable methods to find direction of the search (line search) • Multivariable methods – Quasi-Newton – DFP (Davidon, Fletcher and Powell) – BFGS (Broyden, Fletcher, Goldfarb, and Shanno) – Direct Search – Hill Climbing 13 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Evolutionary Methods • Population-based methods, inspired by biological evolution: reproduction, mutation, recombination and selection • Performs better in locating global or near-global solutions, especially for multimode functions • But suffers one big problem: slow and premature convergence • Solutions: – Hybrid with other efficient gradient-based methods 14 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Handling of Constraints • Eliminate as many constraints as possible using constraint analysis • Use of penalty functions, which is a modified objective function considering the extent to which the constraints are violated. • Multi-objective approach – Use of multi-objective optimization approach by treating each constraint as an objective function 15 p     i   i U U x r h r g © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Dealing with Multiple Objectives (I) • The first type of approach is based on weighted sum method • Solving multi-objective optimization problems using decision making and optimization methods – Converting into single objective problem via weighted sum of multiple objectives 𝑜𝑏𝑗 = ෍𝑤௜𝑓௜ – where, 𝑤௜s are the weight coefficients for the 𝑓௜s are objectives, weights can be fixed before optimization, or varied during the optimization process. – Prior knowledge can be built into the selection of weights, therefore, it is a process consisting of decision making followed by optimization 16 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Dealing with Multiple Objectives(II) • The second type of approach is based on multi-objective methods • Pareto front optimization – Pareto front is the set of all non-dominated solutions, Pareto optimization is the process of finding an approximation to the PF. – Domination 17 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Dealing with Multiple Objectives (III) • Methods to obtain Prato-front – weighted methods, by varying the weight coefficients – Population-based evolutionary methods • NSGA-II • Strength Pareto GA (SPGA) • PESA (Pareto Envelope-based Selection Algorithm • etc. 18

5/16/2018 圆上活文大华 Geometry modeling in aerospace 国上清大学 nacelle,etc.- geometry defined prim direction 外设用 及流叶中可华北设D SIMULATION-BASED DESIGN OPTIMIZATION 藏儿：始设用 General procedures for aircraft geometry definition oorornenin ong Airfoil Parameterization-revisit 国上活美大坐 Forward Fuselage and Wing-body fairing Parameterization 园上活道大整 ·Two examples Y V B-Splime oernan enn ng 图上洋大峰 Wingbody/nacelle/pylon integration上音t大￥ Airframe/Engine Installation 考虑因素 ·发动机系统 聘应面方法 15个样本点 机结构 。吊挂结构 一4个位置参数 ·起落架 机网3nK位置 全局寻优方法 ·系统营路布置 -9个控制面 ·献振 一每个创面14个控制点 几何问题 参数化方法 3个控制面 -10个参数 rslty-Dr.V(enbin Song 4

5/16/2018 4 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics SIMULATION-BASED DESIGN OPTIMIZATION 19 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Geometry modeling in aerospace • Wing Geometry: airfoils, wing, rotor, propeller, tails, canard, pylon, nacelle, etc. – geometry defined primarily along the streamwise direction • Fuselage: fuselage section, revolving bodies, duct, pipe, missile body, nacelle, etc. – geometry defined by cross-section shape 20 General procedures for aircraft geometry definition © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Airfoil Parameterization - revisit © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Forward Fuselage and Wing-body fairing Parameterization • Two examples 22 机头 机翼 平尾 垂尾 小翼 翼身整流罩 滑轨整流罩 机身 增升装置 短舱、挂架 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Airframe/Engine Installation 考虑因素 • 发动机系统 • 机翼结构 • 吊挂结构 • 起落架 • 轮胎爆破 • 系统管路布置 • 颤振 短舱机身干扰边界线 机翼KinK位置 短舱离地高度 侧风起降边界线 地面线 几何问题 通过建模 形成约束 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics • 参数化方法 − 3个控制剖面 − 10个参数 • 全局寻优方法 − 9个控制剖面 − 每个剖面14个控制点 • 响应面方法 − 15个样本点 − 4个位置参数 Wingbody/nacelle/pylon integration 工程实用的 集成的一体化 气动设计方法

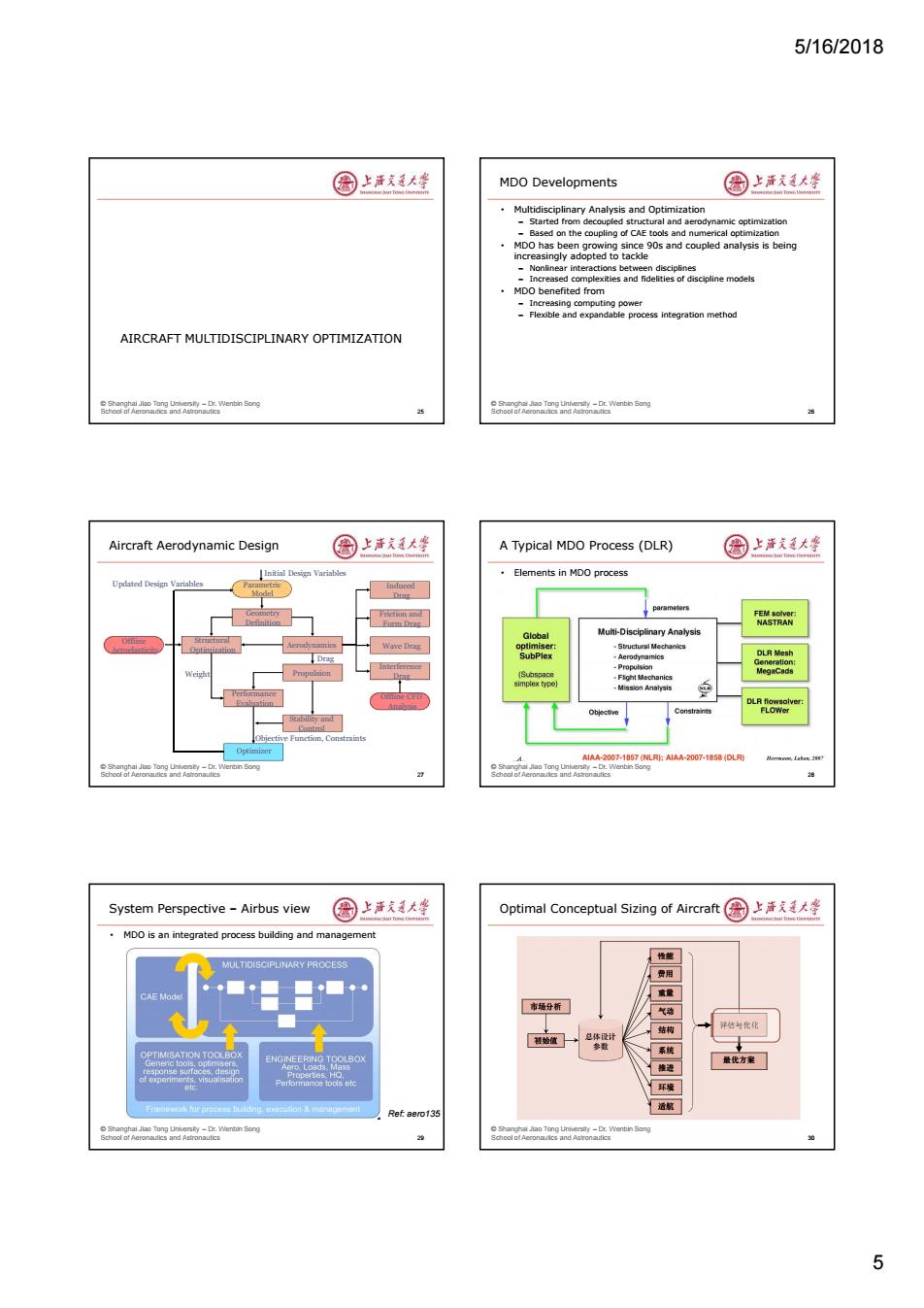
5/16/2018 圆上活文大华 MDO Developments 国上清大学 Multidisciplinary Analysis and Optimization ed str namic optimization MDO has been growing since 90s and coupled analysis is being increasingly adopted to tackle -Nonlinear interactions between disciplines -Increased complexities and fidelities of discipline models .MDO benefited from e ng comp Flexible AIRCRAFT MULTIDISCIPLINARY OPTIMIZATION oorornenin ong orn enin Song Aircraft Aerodynamic Design 圈上活大坐 A Typical MDO Process(DLR) 园上活道大整 Initial Design Variables Elements in MDO process Updated Design Variables Multi-Disciplinary Analysis tural Mechanics DLR Mesh Fight Mechanics Mission Analysis A1A4-2007-1857(LR:A1AA-2007-150DLR 8 System Perspective-Airbus view 图上洋文通大学 Optimal Conceptual Sizing of Aircraft 园上洋文大学 MDO is an integrated process building and management 性能 用 CAE Modr 市场分析 气动 总体设计 结构 评结与优化 始值 参数 ENGINEERING TOOLBOX 系桃 最优方案 航 Ref aero135 Shanghal Jao Tong Unkersty-Dr.Wenbin Song 0 5

5/16/2018 5 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics AIRCRAFT MULTIDISCIPLINARY OPTIMIZATION 25 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics MDO Developments • Multidisciplinary Analysis and Optimization – Started from decoupled structural and aerodynamic optimization – Based on the coupling of CAE tools and numerical optimization • MDO has been growing since 90s and coupled analysis is being increasingly adopted to tackle – Nonlinear interactions between disciplines – Increased complexities and fidelities of discipline models • MDO benefited from – Increasing computing power – Flexible and expandable process integration method 26 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Aircraft Aerodynamic Design 27 Parametric Model Geometry Definition Structural OptimizationPerformance Evaluation Aerodynamics Stability and Control Propulsion Optimizer Induced Drag Friction and Form Drag Wave Drag Interference Drag Offline CFD Analysis Offline Aeroelasticity Initial Design Variables Objective Function, Constraints Drag Weight Updated Design Variables © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics A Typical MDO Process (DLR) • Elements in MDO process 28 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics System Perspective – Airbus view • MDO is an integrated process building and management 29 Ref: aero135 © Shanghai Jiao Tong University – Dr. Wenbin Song School of Aeronautics and Astronautics Optimal Conceptual Sizing of Aircraft 30 气动 结构 推进 系统 环境 评估与优化 总体设计 参数 初始值 最优方案 适航 重量 费用 性能 市场分析