
3.成绩评定: 采用百分制,按以下3项考核指标进行实验成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的30%;(其中考勤占20%,作业占40%,课堂表现占40%) 期中考核成绩:占课程总成绩的10%; 期末考核成绩:占课程总成绩的60%。 八、推荐教材和教学参考书 教材:《电路》.邱关源主编.高等教育出版社,2006年第五版。 参考书:《电路分析基础》,李瀚荪主编,高等教育出版社,2010年第四版 参考书:《电路基础第三版》,亚历山大、萨迪库著,清华大学出版社,2008年改编版 参考书:《电路:学习指导与习题分析》,刘崇新、罗先觉编著,高等教育出版社,2010年 第五版 参考书:《怎样识读电子电路图》,门宏著,人民邮电出版社,2010年 参考书:《Multisim14电路设计与仿真》,吕波编著,机械工业出版社,2016年第一版。 撰写人:程皓 审核人: 学院分管领导签字(盖章): 年月日 14
14 3.成绩评定: 采用百分制,按以下 3 项考核指标进行实验成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的 30%;(其中考勤占 20%,作业占 40%,课堂表现占 40%) 期中考核成绩:占课程总成绩的 10%; 期末考核成绩:占课程总成绩的 60%。 八、推荐教材和教学参考书 教 材:《电路》.邱关源主编. 高等教育出版社,2006 年第五版. 参考书:《电路分析基础》,李瀚荪主编,高等教育出版社,2010 年第四版 参考书:《电路基础第三版》, 亚历山大、 萨迪库著,清华大学出版社,2008 年改编版 参考书:《电路:学习指导与习题分析》,刘崇新、罗先觉编著,高等教育出版社,2010 年 第五版 参考书:《怎样识读电子电路图 》,门宏 著,人民邮电出版社,2010 年 参考书:《Multisim 14 电路设计与仿真》,吕波编著,机械工业出版社,2016 年第一版。 撰写人:程 皓 审核人: 学院分管领导签字(盖章): 年 月 日

《复变函数与积分变换》课程教学大纲 一、课程概况 课程代码:04430080 课程名称:复变函数与积分变换 课程学分:2.5 课程学时:40(理论学时:40;实验(实践)学时:0) 课程性质:学科必修课 开课部门:信息科学与工程学院 建议修读学期:3 建议先修课程:高等数学、大学物理等 适用专业(方向):自动化 二、课程地位、作用与任务 《复变函数与积分变换》是高等学校自动化学科的一门专业基础课程,主要培养学 生的抽象思维能力、逻辑推理能力、空间想象能力和科学计算能力。 本课程的主要任务是使学生能学到复变函数与积分变换中的基本理论及工程技术中 的常用数学方法,同时还可以巩固和复习高等数学的基础知识,为学习有关的后续课程 和进一步扩大数学知识面奠定必要的数学基础,并进一步提高学生的数学素质,及应用 数学知识解决实际问题的能力,以支撑专业毕业要求中相应指标点的达成。 三、课程目标 (一)教学目标 复变函数与积分变换课程具体要求达到的特定教学目标包括: 1教学目标1.使学生掌握复变函数与积分变换的基础理论和运算技能。(指标点1.1) 2教学目标2.使学生可以学到数学物理及工程技术中常用的数学方法,能够运用所学知识 分析复杂问题,并能够建立模型。(指标点12) 3教学目标3.引导学生能应用专业知识用于判别计算过程的极限和优化方案。(指标点1.3) 4教学目标4.能应用间接法将函数进行泰勒或洛朗展开,并能利用留数解决复闭路积分、 定积分和反常积分。(指标点1.4)】 5教学目标5.引导学生能识别和判断计算过程中的关键环节和参数。(指标点2.1) 6教学目标6.通过积分变换的学习能提出问题的不同解决方案。(指标点2.2) (二)本课程支撑的半业要求 1.本课程支撑的毕业要求:(毕业要求1、2。)(毕业要求见2018版人才培养方案) 15
15 《复变函数与积分变换》课程教学大纲 一、课程概况 课程代码:04430080 课程名称:复变函数与积分变换 课程学分:2.5 课程学时:40(理论学时:40;实验(实践)学时:0) 课程性质:学科必修课 开课部门:信息科学与工程学院 建议修读学期:3 建议先修课程:高等数学、大学物理等 适用专业(方向):自动化 二、课程地位、作用与任务 《复变函数与积分变换》是高等学校自动化学科的一门专业基础课程,主要培养学 生的抽象思维能力、逻辑推理能力、空间想象能力和科学计算能力。 本课程的主要任务是使学生能学到复变函数与积分变换中的基本理论及工程技术中 的常用数学方法,同时还可以巩固和复习高等数学的基础知识,为学习有关的后续课程 和进一步扩大数学知识面奠定必要的数学基础,并进一步提高学生的数学素质,及应用 数学知识解决实际问题的能力,以支撑专业毕业要求中相应指标点的达成。 三、课程目标 (一)教学目标 复变函数与积分变换课程具体要求达到的特定教学目标包括: 1 教学目标 1. 使学生掌握复变函数与积分变换的基础理论和运算技能。(指标点 1.1) 2 教学目标 2. 使学生可以学到数学物理及工程技术中常用的数学方法,能够运用所学知识 分析复杂问题,并能够建立模型。(指标点 1.2) 3 教学目标 3. 引导学生能应用专业知识用于判别计算过程的极限和优化方案。(指标点 1.3) 4 教学目标 4. 能应用间接法将函数进行泰勒或洛朗展开,并能利用留数解决复闭路积分、 定积分和反常积分。(指标点 1.4) 5 教学目标 5. 引导学生能识别和判断计算过程中的关键环节和参数。(指标点 2.1) 6 教学目标 6. 通过积分变换的学习能提出问题的不同解决方案。(指标点 2.2) (二)本课程支撑的毕业要求 1. 本课程支撑的毕业要求:(毕业要求 1、2。)(毕业要求见 2018 版人才培养方案)

2.本课程支撑的指标点:指标点1.1、1.2、1.3、1.4、2.1、2.2 (1)指标点11:能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述中。 (2)指标点1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点1.3:能将专业知识和数学模型的方法用于分析、判别过程的极限和优化途径。 (4)指标点1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (5)指标点2.1:能识别和判断复杂工程问题的关键环节和参数。 (6)指标点2.2:能基于科学原理和数学模型方法正确表达工程问题的解决方案。 (三)课程教学目标与半业要求对应表 《复变函数与积分变换》课程教学目标与半业要求的对应表 课程名称:复变函数与积分变换 任课教师:彭兴媛,王晋 课程性质:学科必修课 课程学分:2.5 课程支撑的半业要求 课程目标、达成途径、评价依据 毕业要求1:具备良好的工程知 教学目标1:使学生掌握复变函数与积分变换的基础理 识,能够将数学、自然科学、工 论和运算技能。 程基础和专业知识用于解决自动 达成途径:通过概念讲解使学生掌握复变函数与积分变 化控制系统、自动化测试系统开 换的重点知识、运算技能及应用方法,进而运用复变函 发或集成中的复杂工程问题; 数与积分变换的思想与方法对复杂工程问题进行恰当表 指标点11能将数学、自然科学、 述。 工程基础和专业知识用到复杂工 评价依据:课堂笔记、提问、作业和考试。 程问题的恰当表述中。 毕业要求1:具备良好的工程知 教学目标2:使学生可以学到数学物理及工程技术中常 识,能够将数学、自然科学、工 用的数学方法,能够运用所学知识分析复杂问题,并能 程基础和专业知识用于解决自动 够建立模型。 化控制系统、自动化测试系统开 达成途径:利用解析函数和调和函数的关系,利用调和 发或集成中的复杂工程问题: 函数构建解析函数,并利用偏积分法或线积分法进行求 指标点1.2能针对一个系统或者 解。 过程建立合适的数学模型,并利 评价依据:课堂笔记、提问、作业和考试。 用恰当的方式求解。 毕业要求1:具备良好的工程知 教学目标3:引导学生能应用专业知识用于判别计算过 识,能够将数学、自然科学、工 程的极限和优化方案 程基础和专业知识用于解决自动 达成途径:通过学习函数极限的概念,同时复习高等数 化控制系统、自动化测试系统开 学课程中有关实数域上的极限的知识,加深对极限思想 发或集成中的复杂工程问题; 的理解,并锻炼判断极限存在与否的能力。 指标点13能将专业知识和数学 评价依据:课堂笔记、提问、作业和考试。 模型的方法用于分析、判别过程 的极限和优化途径。 毕业要求1:具备良好的工程知 教学目标4:能应用间接法将函数进行泰勒或洛朗展开, 识,能够将数学、自然科学、工 并能利用留数解决复闭路积分、定积分和反常积分。 程基础和专业知识用于解决自动 达成途径:能计算幂级数的收敛半径及函数的泰勒展开, 化控制系统、自动化测试系统开 并能利用已知函数的泰勒展开式对所给函数进行洛朗展 16
16 2. 本课程支撑的指标点:指标点 1.1、1.2、1.3、1.4、2.1、2.2 (1)指标点 1.1: 能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述中。 (2)指标点 1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点 1.3:能将专业知识和数学模型的方法用于分析、判别过程的极限和优化途径。 (4)指标点 1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (5)指标点 2.1:能识别和判断复杂工程问题的关键环节和参数。 (6)指标点 2.2:能基于科学原理和数学模型方法正确表达工程问题的解决方案。 (三)课程教学目标与毕业要求对应表 《复变函数与积分变换》课程教学目标与毕业要求的对应表 课程名称:复变函数与积分变换 任课教师:彭兴媛,王晋 课程性质:学科必修课 课程学分:2.5 课程支撑的毕业要求 课程目标、达成途径、评价依据 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.1 能将数学、自然科学、 工程基础和专业知识用到复杂工 程问题的恰当表述中。 教学目标 1:使学生掌握复变函数与积分变换的基础理 论和运算技能。 达成途径:通过概念讲解使学生掌握复变函数与积分变 换的重点知识、运算技能及应用方法,进而运用复变函 数与积分变换的思想与方法对复杂工程问题进行恰当表 述。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.2 能针对一个系统或者 过程建立合适的数学模型,并利 用恰当的方式求解。 教学目标 2:使学生可以学到数学物理及工程技术中常 用的数学方法,能够运用所学知识分析复杂问题,并能 够建立模型。 达成途径:利用解析函数和调和函数的关系,利用调和 函数构建解析函数,并利用偏积分法或线积分法进行求 解。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.3 能将专业知识和数学 模型的方法用于分析、判别过程 的极限和优化途径。 教学目标 3:引导学生能应用专业知识用于判别计算过 程的极限和优化方案 达成途径:通过学习函数极限的概念,同时复习高等数 学课程中有关实数域上的极限的知识,加深对极限思想 的理解,并锻炼判断极限存在与否的能力。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 教学目标 4:能应用间接法将函数进行泰勒或洛朗展开, 并能利用留数解决复闭路积分、定积分和反常积分。 达成途径:能计算幂级数的收敛半径及函数的泰勒展开, 并能利用已知函数的泰勒展开式对所给函数进行洛朗展

发或集成中的复杂工程问题: 开;能求出孤立奇点处的留数,进而给出利用围道积分 指标点1.4能用专业知识,通过 法对定积分和反常积分进行计算的方案。 模型比较和综合,优选工程问题 评价依据:课堂笔记、提问、作业和考试。 的解决方案,完成系统的设计和 计算。 毕业要求2:能够应用数学、自 教学目标5:引导学生能识别和判断计算过程中的关键 然科学和工程科学的基本原理, 环节和参数。 识别、表达、并通过文献研究分 达成途径:利用柯西定理、柯西积分公式及其推论确定 析自动化控制系统的复杂工程问 计算闭路积分的关键环节,并在利用参数方程法计算曲 题,以获得有效结论; 线积分时确定其关键参数。 指标点2.1能识别和判断复杂工 评价依据:课堂笔记、提问、作业和考试。 程问题的关键环节和参数。 毕业要求2:能够应用数学、自 教学目标6:通过积分变换的学习能提出问题的不同解 然科学和工程科学的基本原理, 决方案。 识别、表达、并通过文献研究分 达成途径:通过对傅立叶变换和拉普拉斯变换的学习, 析自动化控制系统的复杂工程问 能利用他们的性质建立解决微积分方程的方案。 题,以获得有效结论; 评价依据:课堂笔记、提问、作业和考试。 指标点2.2能基于科学原理和数 学模型方法正确表达工程问题的 解决方案。 四、课程内容 教学内容 作业要求 第一篇复变函数 自学内容:复数的定义及代数运算。 第一章复数与复变函数 1.1复数 课堂作业: 1.2复数的乘幂与方根 讨论实数和复数的区别 1.3平面点集 1.4复变函数 课外作业: 1.5初等函数 1完成本章小结 知识点: 2.练习复数的几种表示方法 1.复数的概念、运算及几何表示,扩充复平 3练习复数的四则运算 面 4练习复数的乘幂和方根的计算 2.复数的乘幂方根,共轭运算 3.复平面上区域、曲线的概念,单连通域, 多连通域。 4.复变函数的概念,几何解释,反函数与复 合函数定义。 5.复数域上的初等函数的定义与性质。 第二章导数 自学内容:复习高等数学中函数极限、连续、 2.1复变函数的极限 导数等概念 2.2复变函数的连续性 2.3导数 课堂作业: 2.4解析函数 讨论复变函数与实变函数的极限、连续、导 17
17 发或集成中的复杂工程问题; 指标点 1.4 能用专业知识,通过 模型比较和综合,优选工程问题 的解决方案,完成系统的设计和 计算。 开;能求出孤立奇点处的留数,进而给出利用围道积分 法对定积分和反常积分进行计算的方案。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 2:能够应用数学、自 然科学和工程科学的基本原理, 识别、表达、并通过文献研究分 析自动化控制系统的复杂工程问 题,以获得有效结论; 指标点 2.1 能识别和判断复杂工 程问题的关键环节和参数。 教学目标 5:引导学生能识别和判断计算过程中的关键 环节和参数。 达成途径:利用柯西定理、柯西积分公式及其推论确定 计算闭路积分的关键环节,并在利用参数方程法计算曲 线积分时确定其关键参数。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 2:能够应用数学、自 然科学和工程科学的基本原理, 识别、表达、并通过文献研究分 析自动化控制系统的复杂工程问 题,以获得有效结论; 指标点 2.2 能基于科学原理和数 学模型方法正确表达工程问题的 解决方案。 教学目标 6:通过积分变换的学习能提出问题的不同解 决方案。 达成途径:通过对傅立叶变换和拉普拉斯变换的学习, 能利用他们的性质建立解决微积分方程的方案。 评价依据:课堂笔记、提问、作业和考试。 四、课程内容 教学内容 作业要求 第一篇 复变函数 第一章 复数与复变函数 1.1 复数 1.2 复数的乘幂与方根 1.3 平面点集 1.4 复变函数 1.5 初等函数 知识点: 1. 复数的概念、运算及几何表示,扩充复平 面 2. 复数的乘幂方根,共轭运算 3. 复平面上区域、曲线的概念,单连通域, 多连通域。 4. 复变函数的概念,几何解释,反函数与复 合函数定义。 5. 复数域上的初等函数的定义与性质。 自学内容:复数的定义及代数运算。 课堂作业: 讨论实数和复数的区别 课外作业: 1.完成本章小结 2.练习复数的几种表示方法 3.练习复数的四则运算 4.练习复数的乘幂和方根的计算 第二章 导数 2.1 复变函数的极限 2.2 复变函数的连续性 2.3 导数 2.4 解析函数 自学内容:复习高等数学中函数极限、连续、 导数等概念 课堂作业: 讨论复变函数与实变函数的极限、连续、导
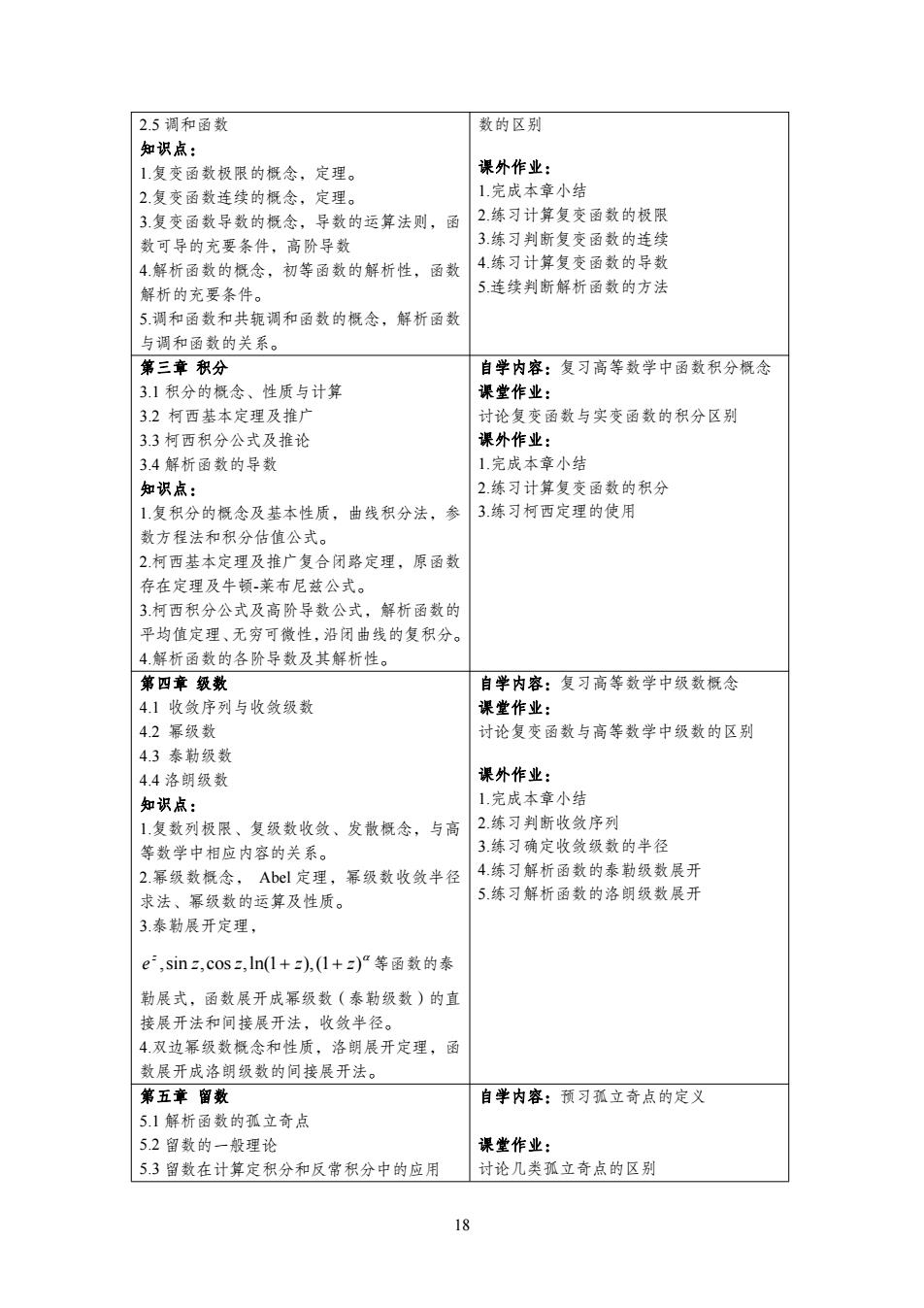
2.5调和函数 数的区别 知识点: 1复变函数极限的概念,定理。 课外作业: 2.复变函数连续的概念,定理。 1完成本章小结 3复变函数导数的概念,导数的运算法则,函 2.练习计算复变函数的极限 数可导的充要条件,高阶导数 3练习判断复变函数的连续 4.解析函数的概念,初等函数的解析性,函数 4.练习计算复变函数的导数 解析的充要条件。 5.连续判断解析函数的方法 5.调和函数和共轭调和函数的概念,解析函数 与调和函数的关系。 第三章积分 自学内容:复习高等数学中函数积分概念 3.1积分的概念、性质与计算 课堂作业: 32柯西基本定理及推广 讨论复变函数与实变函数的积分区别 3.3柯西积分公式及推论 课外作业: 3.4解析函数的导数 1.完成本章小结 知识点: 2.练习计算复变函数的积分 1.复积分的概念及基本性质,曲线积分法,参 3.练习柯西定理的使用 数方程法和积分估值公式。 2柯西基本定理及推广复合闭路定理,原函数 存在定理及牛顿-莱布尼兹公式。 3柯西积分公式及高阶导数公式,解析函数的 平均值定理、无穷可微性,沿闭曲线的复积分。 4解析函数的各阶导数及其解析性。 第四章级数 自学内容:复习高等数学中级数概念 4.1收敛序列与收敛级数 课堂作业: 4.2幂级数 讨论复变函数与高等数学中级数的区别 4.3泰勒级数 4.4洛朗级数 课外作业: 知识点: 1完成本章小结 1复数列极限、复级数收敛、发散概念,与高 2.练习判断收敛序列 等数学中相应内容的关系。 3.练习确定收敛级数的半径 2.幂级数概念,Abel定理,幂级数收敛半径 4.练习解析函数的泰勒级数展开 求法、幂级数的运算及性质。 5.练习解析函数的洛朗级数展开 3泰勒展开定理, e,sinz,cosz,ln(1+z),(1+z)“等函数的泰 勒展式,函数展开成幂级数(泰勒级数)的直 接展开法和间接展开法,收敛半径。 4双边幂级数概念和性质,洛朗展开定理,函 数展开成洛朗级数的间接展开法。 第五章留数 自学内容:预习孤立奇点的定义 5.1解析函数的孤立奇点 5.2留数的一般理论 课堂作业: 5.3留数在计算定积分和反常积分中的应用 讨论几类孤立奇点的区别 18
18 2.5 调和函数 知识点: 1.复变函数极限的概念,定理。 2.复变函数连续的概念,定理。 3.复变函数导数的概念,导数的运算法则,函 数可导的充要条件,高阶导数 4.解析函数的概念,初等函数的解析性,函数 解析的充要条件。 5.调和函数和共轭调和函数的概念,解析函数 与调和函数的关系。 数的区别 课外作业: 1.完成本章小结 2.练习计算复变函数的极限 3.练习判断复变函数的连续 4.练习计算复变函数的导数 5.连续判断解析函数的方法 第三章 积分 3.1 积分的概念、性质与计算 3.2 柯西基本定理及推广 3.3 柯西积分公式及推论 3.4 解析函数的导数 知识点: 1.复积分的概念及基本性质,曲线积分法,参 数方程法和积分估值公式。 2.柯西基本定理及推广复合闭路定理,原函数 存在定理及牛顿-莱布尼兹公式。 3.柯西积分公式及高阶导数公式,解析函数的 平均值定理、无穷可微性,沿闭曲线的复积分。 4.解析函数的各阶导数及其解析性。 自学内容:复习高等数学中函数积分概念 课堂作业: 讨论复变函数与实变函数的积分区别 课外作业: 1.完成本章小结 2.练习计算复变函数的积分 3.练习柯西定理的使用 第四章 级数 4.1 收敛序列与收敛级数 4.2 幂级数 4.3 泰勒级数 4.4 洛朗级数 知识点: 1.复数列极限、复级数收敛、发散概念,与高 等数学中相应内容的关系。 2.幂级数概念, Abel 定理,幂级数收敛半径 求法、幂级数的运算及性质。 3.泰勒展开定理, e ,sin z, cos z,ln(1 z),(1 z) z 等函数的泰 勒展式,函数展开成幂级数(泰勒级数)的直 接展开法和间接展开法,收敛半径。 4.双边幂级数概念和性质,洛朗展开定理,函 数展开成洛朗级数的间接展开法。 自学内容:复习高等数学中级数概念 课堂作业: 讨论复变函数与高等数学中级数的区别 课外作业: 1.完成本章小结 2.练习判断收敛序列 3.练习确定收敛级数的半径 4.练习解析函数的泰勒级数展开 5.练习解析函数的洛朗级数展开 第五章 留数 5.1 解析函数的孤立奇点 5.2 留数的一般理论 5.3 留数在计算定积分和反常积分中的应用 自学内容:预习孤立奇点的定义 课堂作业: 讨论几类孤立奇点的区别