
2.1.2离散LTI系统的单位脉冲响应及卷积和表示 (1)单位脉冲响应 x[nl=δn] y[n]=h[n] LTI h[n:单位脉冲响应 第2章线性时不变系统 11
第2章 线性时不变系统 11 (1) 单位脉冲响应 LTI x[n]=δ[n] y[n]=h[n] h[n]:单位脉冲响应 2.1.2离散LTI系统的单位脉冲响应及卷积和表示
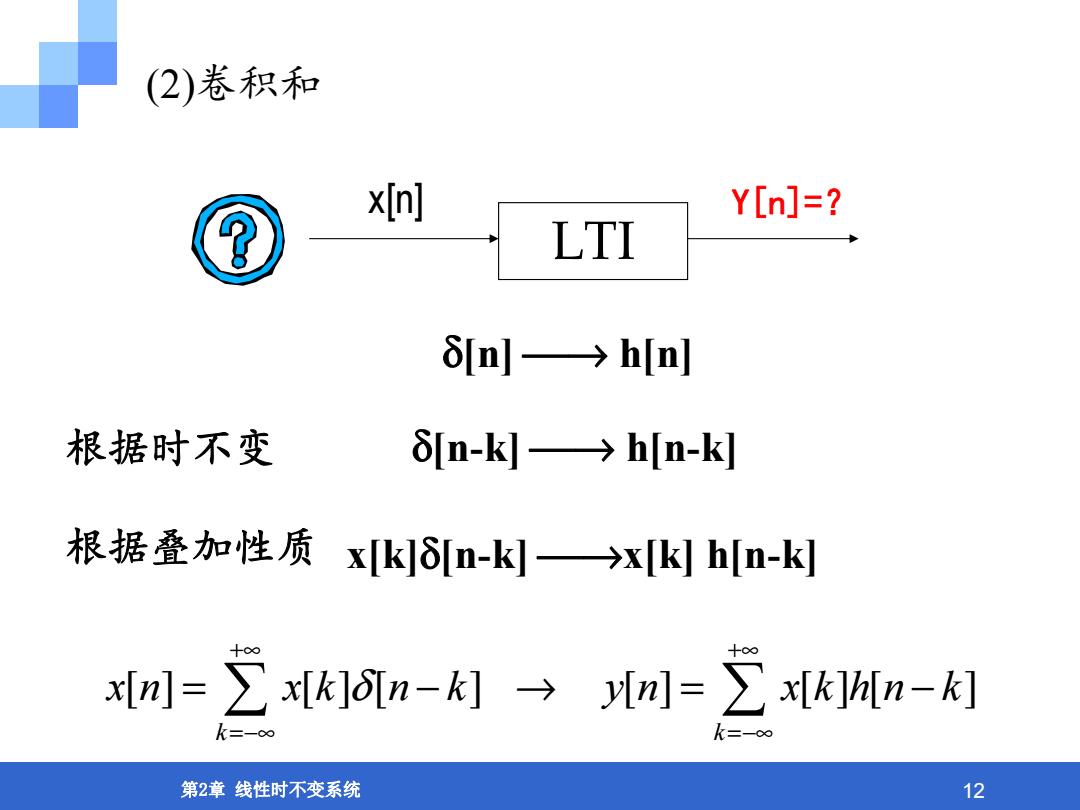
(2)卷积和 xIn] Y[n]=? ⑧ LTI δ[n→h[nl 根据时不变 δ[n-k→h[n-k 根据叠加性质 x[kδ[n-k→x[khn-k [n=∑x[k]n-k→m=∑x[k]hM[n-k] k=-∞ k=-o∞ 第2章线性时不变系统 12
第2章 线性时不变系统 12 δ[n] ⎯→ h[n] [] [][ ] [] [][ ] k k x n xk n k yn xkhn k δ +∞ +∞ =−∞ =−∞ = −→ = − (2)卷积和 LTI x[n] Y[n]=? 根据时不变 δ[n-k] ⎯→ h[n-k] 根据叠加性质 x[k]δ[n-k] ⎯→x[k] h[n-k]
举例说明式2.3的意义。下图示出该系统对6[n+1 6[m和6[n-1的响应是hn,ho[m和hn。 xin] 钩 h-1in) ho In] h,[n (b) 图2,2由(23)式表示的离散时间线性系统响应的图解浅示
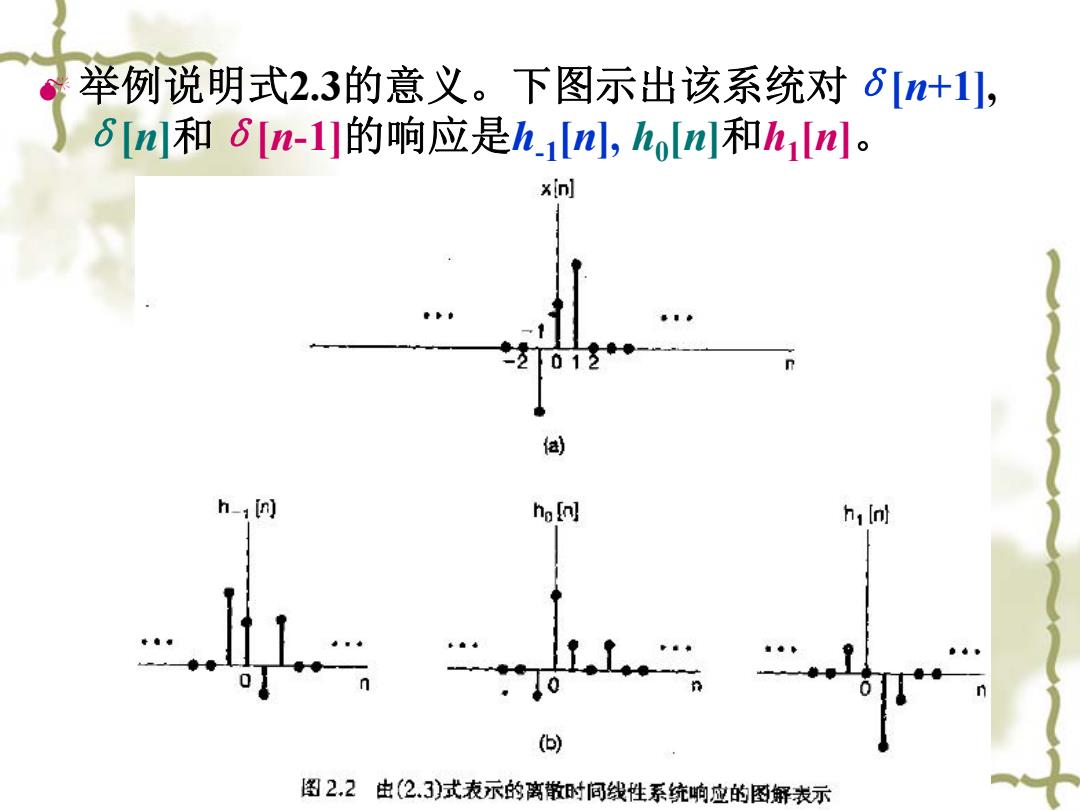
举例说明式2.3的意义。下图示出该系统对 δ [ n+1], δ [ n ] 和 δ [ n-1]的响应是 h-1 [ n], h0 [ n ] 和 h1 [ n ]

对-118+1 x-1h-问 x[n]=x[-1]Ln+1] +x[0]n] x08 x[a]holn] +x[1][n-1] 1n-1j x们h坷 y[n]=x[-1]h[n] +x[0]h[n] +x[1]h[n
[ ] [ 1] [ 1] [0] [ ] [1] [ 1] xn x n x n x n δ δ δ =− + + + − 1 0 1 [ ] [ 1] [ ] [0] [ ] [1] [ ] y n x hn x hn x hn = − − + +

一般说来,在线性系统中,对于不同的值,其响 应hn相互之间是没必要非有什么关系不可。但是 若该系统也是时不变的,就有:因为6[-k是6[ 的时移,响应hn川也就是hm川的一个时移,即 hkn]holn-k] 为了简化符号,将m下标去掉,而定义系统单位 脉冲(样本)序列响应为 h(n]holn] 也就是说,n是LTI系统当输入为δ[n时的输 出。 Ln→LTI系统→hMn]
一般说来,在线性系统中,对于不同的 k值,其响 应 h k [ n ]相互之间是没必要非有什么关系不可。但是 若该系统也是时不变的,就有:因为 δ [ n - k ] 是 δ [ n] 的时移,响应 hk [ n ]也就是 h0 [ n ]的一个时移,即 hk [ n] = h0 [ n - k ] 为了简化符号,将 h0 [ n ]下标去掉,而定义系统单位 脉冲(样本)序列响应为 h [ n] = h0 [ n ] 也就是说, h [ n ] 是LTI系统当输入为 δ [ n ]时的输 出。 δ[ ] LTI [ ] n hn → → 系统