边的染色 ■对于任意一个二分图G:X(G=△(G) ●若不存在i=j,即i卡j 则关联一条色为的边 ●对于G-(w,v)中 以为起点、交替经过色为和的边的极长路线P, P是一条路,且不经过v 2023/5/15 26
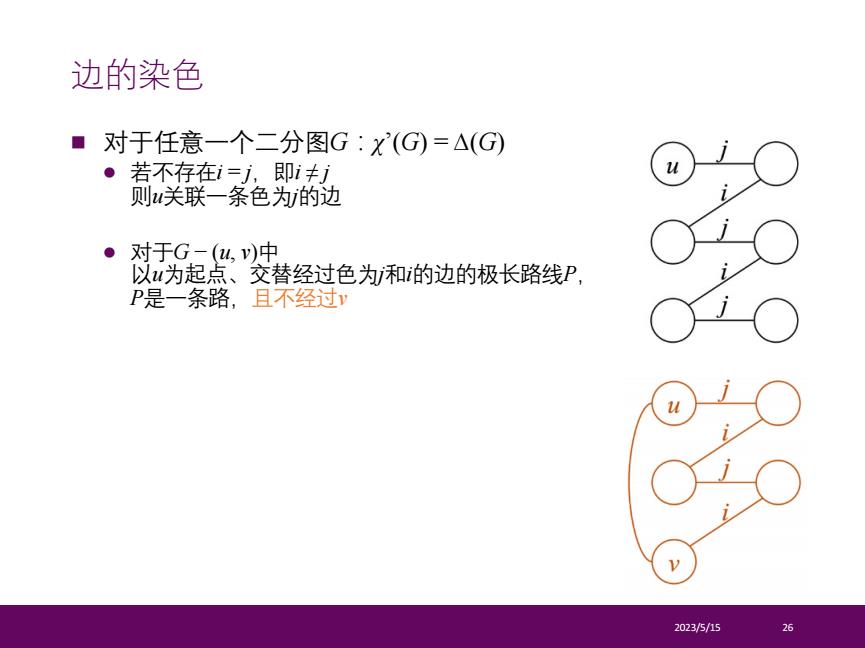
n 对于任意一个二分图G:χ’(G) = ∆(G) l 若不存在i = j,即i ≠ j 则u关联一条色为j的边 l 对于G − (u, v)中 以u为起点、交替经过色为j和i的边的极长路线P, P是一条路,且不经过v 2023/5/15 26 边的染色
边的染色 ■对于任意一个二分图G:X(G=△(G) ● 若不存在i=j,即ij 则关联一条色为的边 ●对于G-(4,v)中 以为起点、交替经过色为j和的边的极长路线P, P是一条路,且不经过v 离 “翻转”P经过的边的色 得到G-(4,v)的另一个正常(G-(u,)边染色 且X(G-(u,v)≤△(G 且u和关联的边都没有染过色j 2023/5/15 27
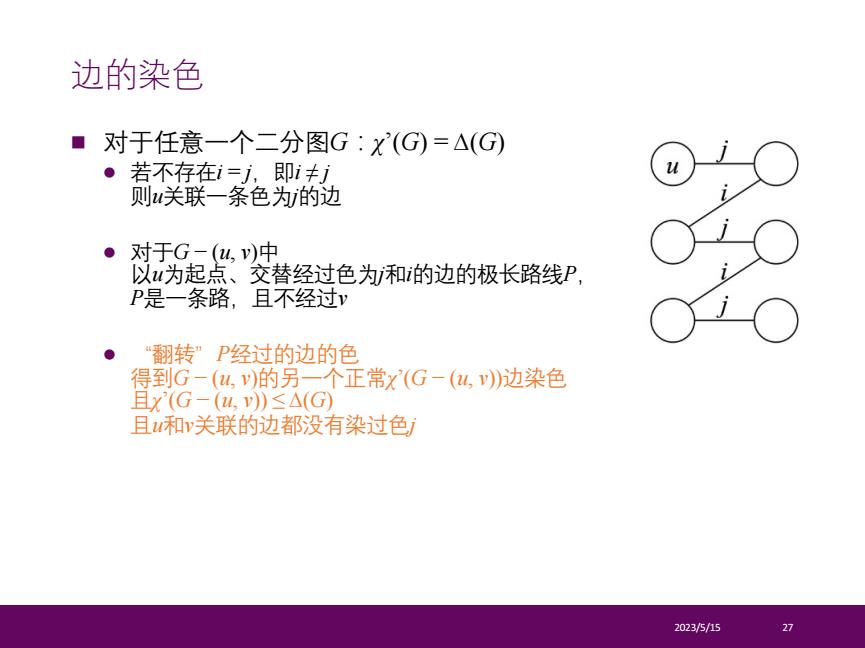
n 对于任意一个二分图G:χ’(G) = ∆(G) l 若不存在i = j,即i ≠ j 则u关联一条色为j的边 l 对于G − (u, v)中 以u为起点、交替经过色为j和i的边的极长路线P, P是一条路,且不经过v l “翻转”P经过的边的色 得到G − (u, v)的另一个正常χ’(G − (u, v))边染色 且χ’(G − (u, v)) ≤ ∆(G) 且u和v关联的边都没有染过色j 2023/5/15 27 边的染色

边的染色 ■对于任意一个图G:△(G)≤X(G)≤△(G)+1 2023/5/15 28
n 对于任意一个图G:∆(G) ≤ χ’(G) ≤ ∆(G) + 1 2023/5/15 28 边的染色

边的染色 ■Vadim Georgievich Vizing,1937年出生于苏联 https::/do.org10.1007/978-0-387-74642-516 2023/5/15 29
n Vadim Georgievich Vizing,1937年出生于苏联 2023/5/15 29 边的染色 https://doi.org/10.1007/978-0-387-74642-5_16

边的染色 ■对于任意一个图G:△(G)≤X(G)≤△(G)+1 ·第一个不等式:显然 ·第二个不等式:构造法证明(算法)】 2023/5/15 30
n 对于任意一个图G:∆(G) ≤ χ’(G) ≤ ∆(G) + 1 l 第一个不等式:显然 l 第二个不等式:构造法证明(算法) 2023/5/15 30 边的染色