边的染色 ■对于任意一个二分图G:X(G)=△(G) ●1 假设(G=k时成立 则(G=k+I时,构造G的正常k边染色且k≤△(G) ●对于G中任意一条边(u,v),由归纳假设 存在G-(u,v)的正常x(G-(u,)边染色 且y(G-(u,)≤△(G-(u,v)≤△(G) 2023/5/15 21
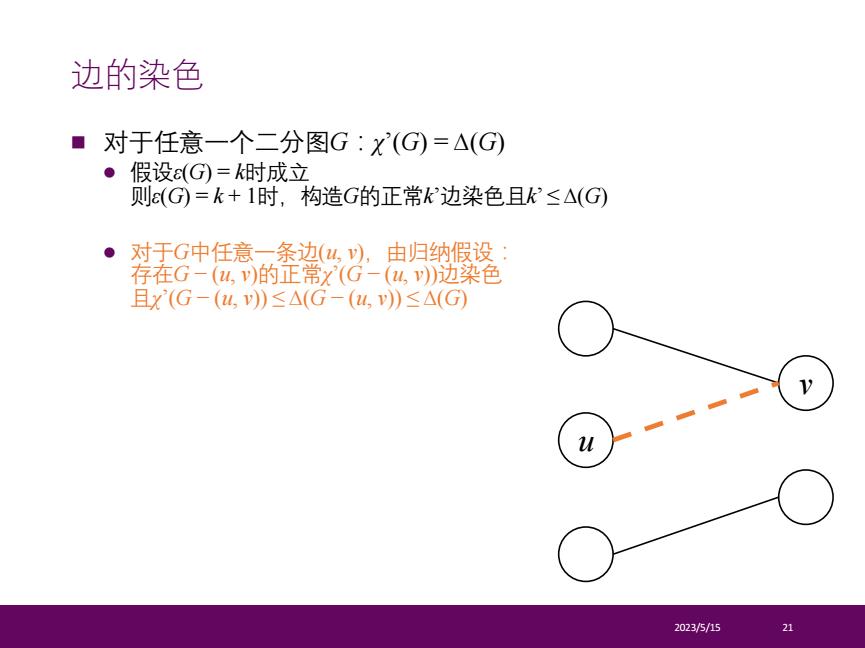
n 对于任意一个二分图G:χ’(G) = ∆(G) l 假设ε(G) = k时成立 则ε(G) = k + 1时,构造G的正常k’边染色且k’ ≤ ∆(G) l 对于G中任意一条边(u, v),由归纳假设: 存在G − (u, v)的正常χ’(G − (u, v))边染色 且χ’(G − (u, v)) ≤ ∆(G − (u, v)) ≤ ∆(G) 2023/5/15 21 边的染色 u v
边的染色 ■对于任意一个二分图G:X(G)=△(G) ●假设(G=k时成立 则(G=k+I时,构造G的正常k边染色且k≤△(G) ·对于G中任意一条边(u,),由归纳假设: 存在G-(u,v)的正常x(G-(u,v)边染色 且X(G-(u,)≤△(G-(u,v)≤△(G ●在G-(u,v)中,存在色1≤i,j≤△(G, u关联的边没有染过色1 v关联的边没有染过色) 2023/5/15 之
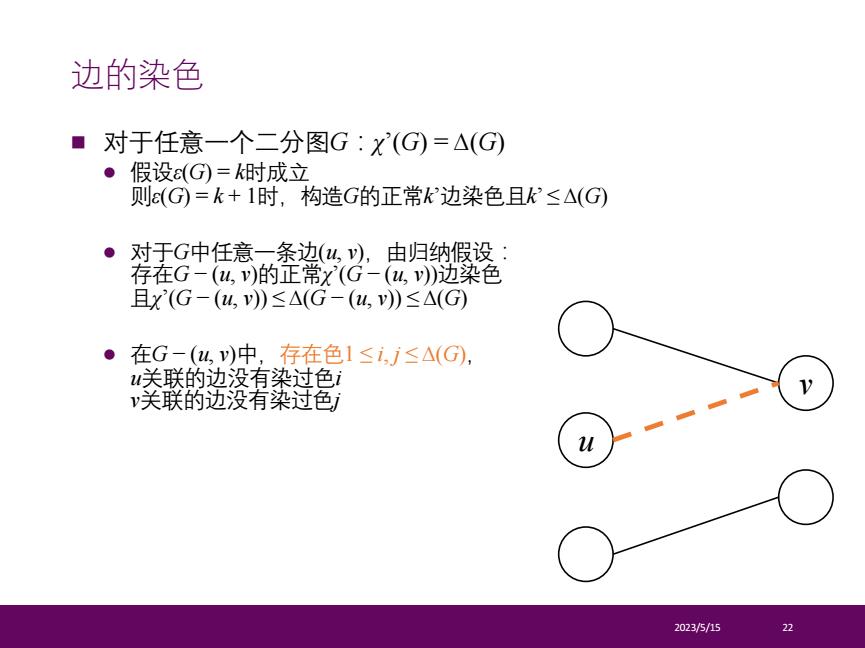
n 对于任意一个二分图G:χ’(G) = ∆(G) l 假设ε(G) = k时成立 则ε(G) = k + 1时,构造G的正常k’边染色且k’ ≤ ∆(G) l 对于G中任意一条边(u, v),由归纳假设: 存在G − (u, v)的正常χ’(G − (u, v))边染色 且χ’(G − (u, v)) ≤ ∆(G − (u, v)) ≤ ∆(G) l 在G − (u, v)中,存在色1 ≤ i, j ≤ ∆(G), u关联的边没有染过色i v关联的边没有染过色j 2023/5/15 22 边的染色 u v
边的染色 ■对于任意一个二分图G:X(G=△(G) ●1 假设(G)=k时成立 则(G)=k+1时,构造G的正常k边染色且k≤△(G) ·对于G中任意一条边(4,),由归纳假设: 存在G-(4,v)的正常x(G-(4,)边染色 且x(G-(u,)≤△(G-(u,v)≤△(G) ●在G-(w,)中,存在色1≤i,j≤△(G), u关联的边没有染过色i v关联的边没有染过色) ●若i=j 则如何得到G的正常k边染色且≤△(G⑦? 2023/5/15 23
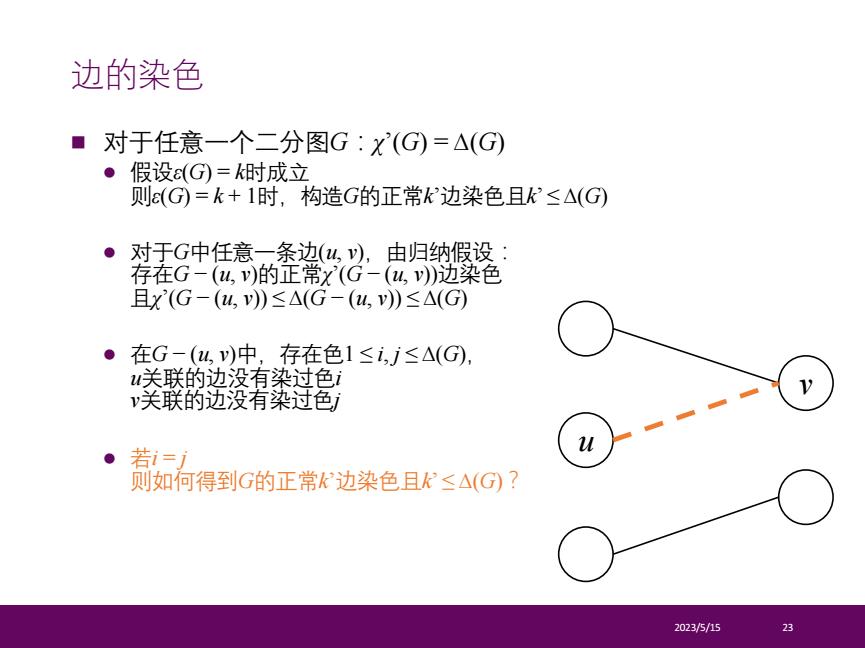
n 对于任意一个二分图G:χ’(G) = ∆(G) l 假设ε(G) = k时成立 则ε(G) = k + 1时,构造G的正常k’边染色且k’ ≤ ∆(G) l 对于G中任意一条边(u, v),由归纳假设: 存在G − (u, v)的正常χ’(G − (u, v))边染色 且χ’(G − (u, v)) ≤ ∆(G − (u, v)) ≤ ∆(G) l 在G − (u, v)中,存在色1 ≤ i, j ≤ ∆(G), u关联的边没有染过色i v关联的边没有染过色j l 若i = j 则如何得到G的正常k’边染色且k’ ≤ ∆(G)? 2023/5/15 23 边的染色 u v

边的染色 ■对于任意一个二分图G:X(G)=△(G) ●若不存在i=广,即i卡) 则关联一条色为的边 2023/5/15 24
n 对于任意一个二分图G:χ’(G) = ∆(G) l 若不存在i = j,即i ≠ j 则u关联一条色为j的边 2023/5/15 24 边的染色
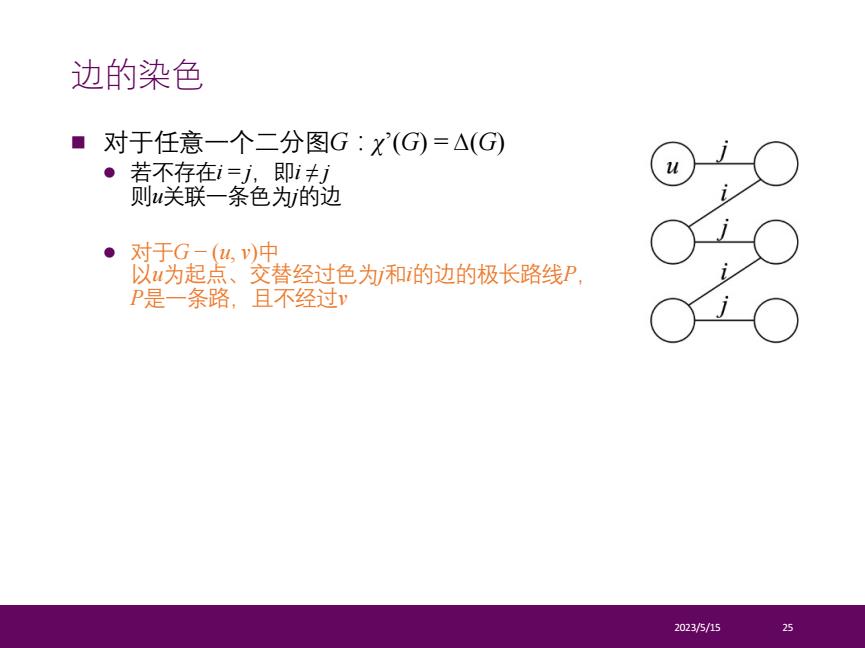
边的染色 ■对于任意一个二分图G:X(G=△(G) ● 若不存在i=j,即ij 则关联一条色为的边 ●对于G-(u,)中 以为起点、交替经过色为和的边的极长路线P, P是一条路,且不经过v 2023/5/15 25
n 对于任意一个二分图G:χ’(G) = ∆(G) l 若不存在i = j,即i ≠ j 则u关联一条色为j的边 l 对于G − (u, v)中 以u为起点、交替经过色为j和i的边的极长路线P, P是一条路,且不经过v 2023/5/15 25 边的染色