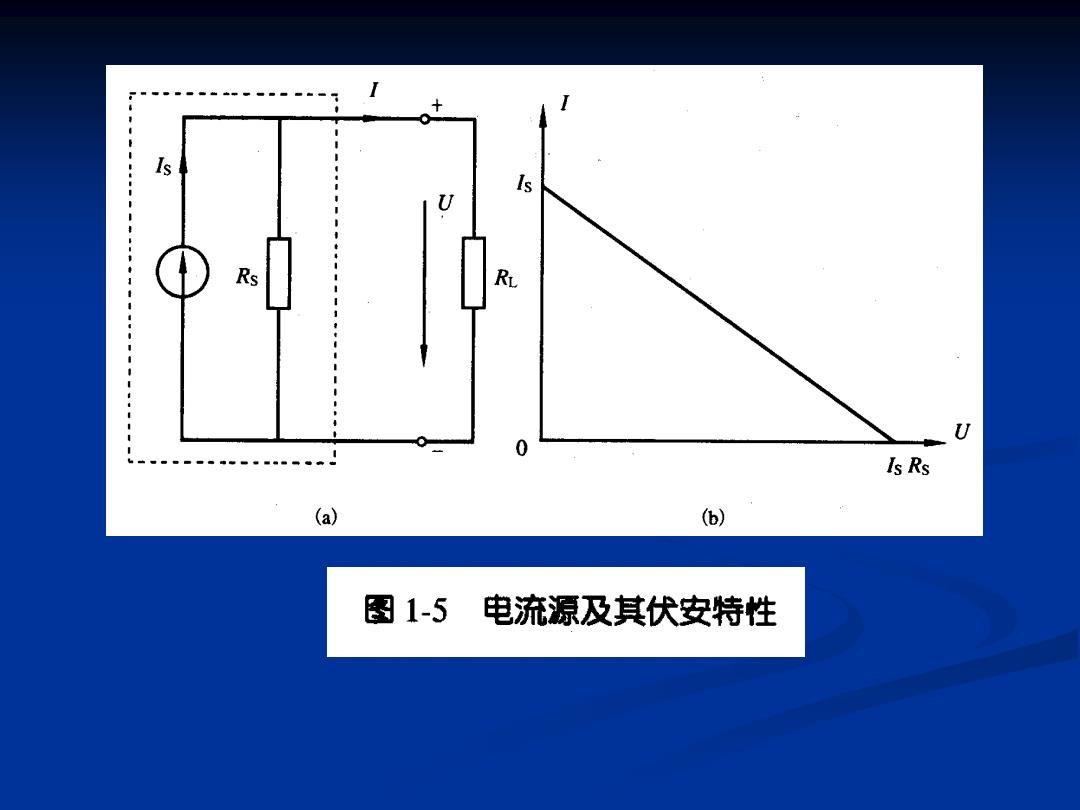
Is Is U Rs R U 0 Is Rs (a) (6) 图1-5 电流源及其伏安特性

在电流源内阻R。=O的情况下, 式(1=5)中的输出电流I将恒 等于I。,而不随负载电阻R 的变动而变化,称为理想电 流源或恒流源,伏安特性如 图1-5(c)所示。 Is 实际中,如果电流源内阻Rs 远大于负载电阻R时,可近 似地看成是恒流源。 ·从上面的讨论可以看出,为 U 了使电压源和电流源更接近 理想的电压源和电流源,电 (c) 压源的内阻R应越小越好, 而电流源的内阻R。应越大越 好
◼ 在电流源内阻Rs =∞的情况下, 式(1-5)中的输出电流I将恒 等于Is,而不随负载电阻RL 的变动而变化,称为理想电 流源或恒流源,伏安特性如 图1-5(c)所示。 ◼ 实际中,如果电流源内阻Rs 远大于负载电阻RL时,可近 似地看成是恒流源。 ◼ 从上面的讨论可以看出,为 了使电压源和电流源更接近 理想的电压源和电流源,电 压源的内阻R0应越小越好, 而电流源的内阻Rs应越大越 好

3.电压源与电流源的等效变换 在简化电路分析时,有时需要将电压源变 换成电流源,或者将电流源变换成电压源。但 不管怎样变换,对负载R来说,应当都有相同 的输出电流和输出电压U,即进行等效变换 等效变换的条件是 I.=E/Ro>Rs=Ro 只要给出了电源的一种电路模型的参数, 就可以根据等效变换的条件将它转换成另一种 电路模型
3.电压源与电流源的等效变换 在简化电路分析时,有时需要将电压源变 换成电流源,或者将电流源变换成电压源。但 不管怎样变换,对负载RL来说,应当都有相同 的输出电流I和输出电压U,即进行等效变换。 等效变换的条件是: Is=E/R0 , Rs=R0 只要给出了电源的一种电路模型的参数, 就可以根据等效变换的条件将它转换成另一种 电路模型.

四.戴维南定理 在一个电路中,往往只要计算其中某一支路的 电流或电压,这样,相对于该支路图来说,电路的 其余部分只有两个端点与它连接。不管其余部分电 路的内部结构如何复杂,都可以将它用一个等效电 源来代替,这样就能将复杂电路化为简单回路求解 如果用等效电源替代的那部分电路中含有电源, 且有两个出线端,则称它为有源二端网络,又称为 含源二端网络;如果二端网络中不含有电源,则称 为无源二端网络
四. 戴维南定理 在一个电路中,往往只要计算其中某一支路的 电流或电压,这样,相对于该支路图来说,电路的 其余部分只有两个端点与它连接。不管其余部分电 路的内部结构如何复杂,都可以将它用一个等效电 源来代替,这样就能将复杂电路化为简单回路求解。 如果用等效电源替代的那部分电路中含有电源, 且有两个出线端,则称它为有源二端网络,又称为 含源二端网络;如果二端网络中不含有电源,则称 为无源二端网络

戴维南定理指出:任何一个含源线性二 端网络均可以等效成为一个电压源。 这个电压源的电动势E,等于该含源二 端网络的开路电压即该二端网络与外电路 断开时其两端点之间的电压),而内阻R则等 于此二端网络内部所有电源都为零时(即全 部电压源短路,电流源开路)的两个输出端 点之间的等效电阻
戴维南定理指出:任何一个含源线性二 端网络均可以等效成为一个电压源。 这个电压源的电动势E’,等于该含源二 端网络的开路电压(即该二端网络与外电路 断开时其两端点之间的电压),而内阻R’则等 于此二端网络内部所有电源都为零时(即全 部电压源短路,电流源开路)的两个输出端 点之间的等效电阻