二.基尔霍夫定律(K irchhoff's Law) R3 用于进行复杂电路的计算。 支路(branch):通过同一电流 的每个分支电路。 节点(nodal point):二条或三 条以上通电支路的汇合点。 1.基尔霍夫第一定律 图1-2支路和节点 流入节点的电流之和等于流 出节点电流之和。 I=11+L2 -I1I2=0
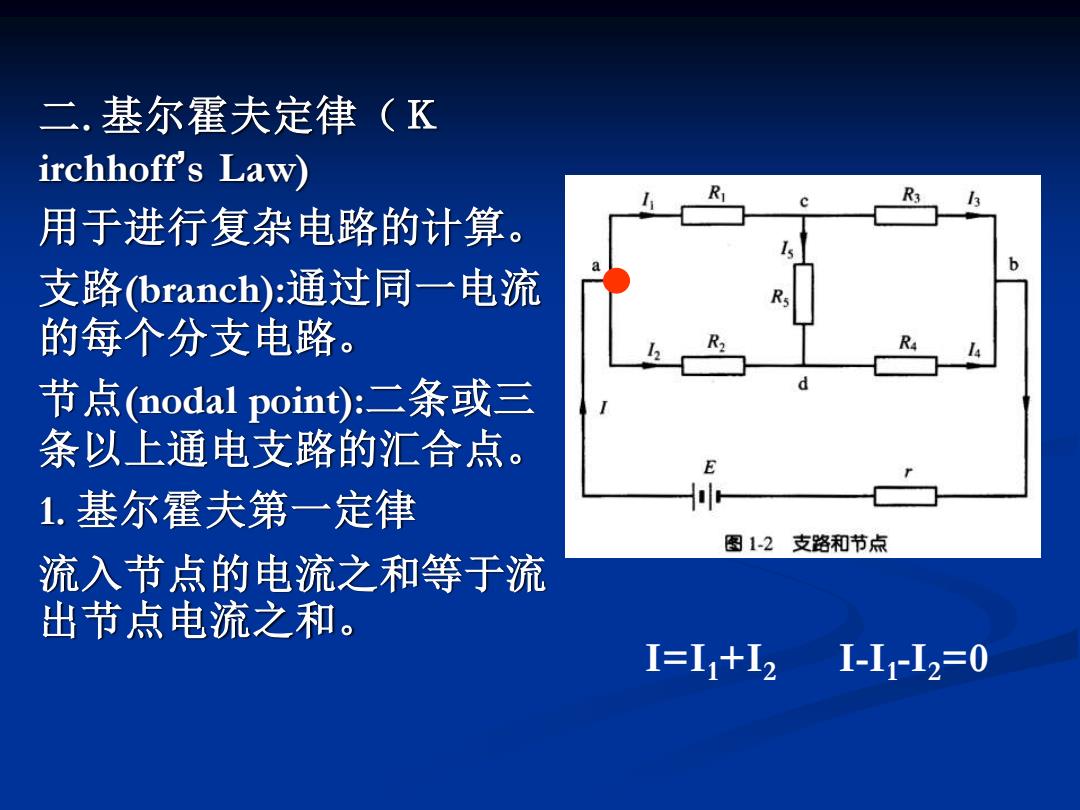
二. 基尔霍夫定律(K irchhoff’s Law) 用于进行复杂电路的计算。 支路(branch):通过同一电流 的每个分支电路。 节点(nodal point):二条或三 条以上通电支路的汇合点。 1. 基尔霍夫第一定律 流入节点的电流之和等于流 出节点电流之和。 I=I1+I2 I-I1 -I2=0

对于各节点应用基尔霍夫第一定律可以写出 一组电流方程, 称为基尔霍夫第一方程组, 通常记为∑I=0 其中流入节点的电流规定为正,流出节点的 电流为负。在应用第一定律时,如果支路电 流的方向不能预先确定,可以先任意假定一 个方向,最后由计算结果来确定它的实际方 向,如果计算值为正, 则实际方向与假设方 向相同;如果计算值为负,则实际方向与假 设方向相反
◼ 对于各节点应用基尔霍夫第一定律可以写出 一组电流方程,称为基尔霍夫第一方程组, 通常记为∑I=0 ◼ 其中流入节点的电流规定为正,流出节点的 电流为负。在应用第一定律时,如果支路电 流的方向不能预先确定,可以先任意假定一 个方向,最后由计算结果来确定它的实际方 向,如果计算值为正,则实际方向与假设方 向相同;如果计算值为负,则实际方向与假 设方向相反

2.基尔霍夫第二定律 在分支电路中,任一闭合路径称为回路 (1oop),如图13所示,abdca和abfea都是闭 合回路 ■基尔霍夫第二定律指出:沿任一闭合回路的 电势增量的代数和等于零。即∑E+∑IR=0 ■对于各闭合回路,应用基尔霍夫第二定律可 以列出一组电压方程,称为基尔霍夫第二方 程组
2. 基尔霍夫第二定律 ◼ 在分支电路中,任一闭合路径称为回路 (1oop),如图1-3所示,abdca和abfea都是闭 合回路。 ◼ 基尔霍夫第二定律指出:沿任一闭合回路的 电势增量的代数和等于零。即 ∑E+∑IR=0 ◼ 对于各闭合回路,应用基尔霍夫第二定律可 以列出一组电压方程,称为基尔霍夫第二方 程组

在使用基尔霍夫定律求解时,电流的 方向和绕行方向是任意选定的,并规定 电势升高者为“+”,电势降低者为 “_ 具体按以下规则确定电势增量的正、 负号:①当电阻R中的电流方向与选定的 回路绕行方向相反时,电势增量为+R, 相同时,电势增量为R;②如果电动势E 从负极到正极的方向与选定的绕行方向相 同,则电势增量为+E,相反时,电势增量 为-E
在使用基尔霍夫定律求解时,电流的 方向和绕行方向是任意选定的,并规定, 电势升高者为“+”,电势降低者为“-” 。 具体按以下规则确定电势增量的正、 负号:①当电阻R中的电流方向与选定的 回路绕行方向相反时,电势增量为+IR, 相同时,电势增量为-IR;②如果电动势E 从负极到正极的方向与选定的绕行方向相 同,则电势增量为+E,相反时,电势增量 为-E
电路如图13所示。 E E1=4.0V,E2=6.0V,R=1.02,R2=1.52,R3=10 2,计算I1,I2,I3的值。 解:假设各支路的电流方向如图中的箭头所 b 示,根据基尔霍夫第一定律,对于节点a,有 1+I2I30(a) 根据基尔霍夫第二定律,对于回路dcabd(逆 时针方向),有 图13选取闭合回路 E1-I1R1+I2R2E2=0(b) 对于回路abfea(顺时针方向),有 I2R2-E2+I3R30(c) 将(a)、(b)、(c)三式联立,通过对方程组 求解,可得各支路的电流分别为 I-0.53A I2=0.98A I3=0.45A
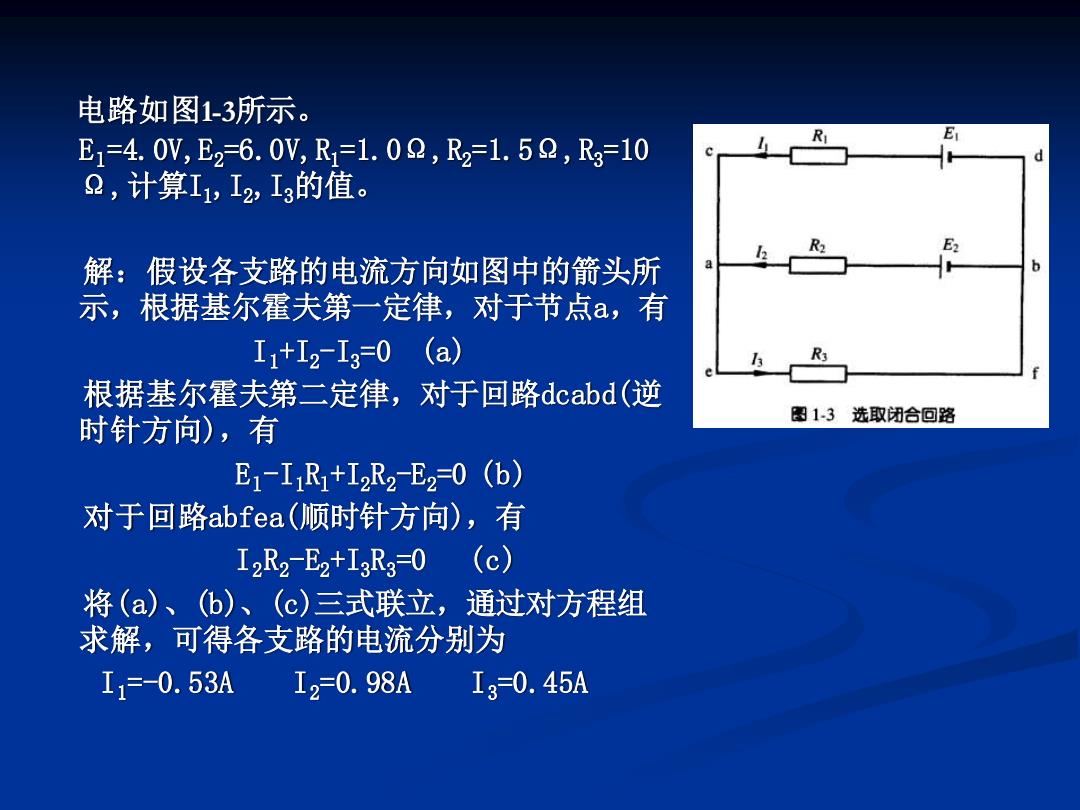
电路如图1-3所示。 El=4.0V,E2=6.0V,R1=1.0Ω,R2=1.5Ω,R3=10 Ω,计算I1,I2,I3的值。 解:假设各支路的电流方向如图中的箭头所 示,根据基尔霍夫第一定律,对于节点a,有 I1+I2-I3=0 (a) 根据基尔霍夫第二定律,对于回路dcabd(逆 时针方向),有 El-I1Rl+I2R2-E2=0 (b) 对于回路abfea(顺时针方向),有 I2R2-E2+I3R3=0 (c) 将(a)、(b)、(c)三式联立,通过对方程组 求解,可得各支路的电流分别为 I1=-0.53A I2=0.98A I3=0.45A